|
Шпаргалка По Математической Логике К Экзамену Для Дневников (Дьячков А. М.). Шпаргалка По Математической Логике К Экзамену Для Дневников (Дья. 1. Алгебра высказываний пропозициональные связки и формы, истинностные таблицы Высказывание
1.Алгебра высказываний; пропозициональные связки и формы, истинностные таблицы
Высказывание – повествовательное предложение, о котором можно сказать, истинно оно или ложно. Значение «истинно» и «ложно» обычно обозначаются 1 или 0, или И и Л.
Содержательно логические операции обычно интерпретируют следующим образом:
отрицание (инверсия)¬ (− ) − «не»
дизъюнкция 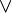 − «или» − «или»
конъюнкция & (А&B или A.В) − «и»
импликация → − «если … , то»
эквивалентность − «тогда и только тогда» (или «эквивалентно»)
приоритеты по выполнению действий: ¬, &, 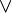 , →, , →,
.
Символы ¬, &, 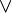 , →, , →,
наз-ся пропозициональными(или логическими) связками. Буквы, обозначающие высказывания, наз-ся пропозициональными буквами. Осмысленные формулы, составленные из пропозициональных букв, пропозициональных связок, а также скобок, указывающих порядок выполнения операций, наз-ся пропозициональными формами(ПФ).
Операции логики высказываний можно задать с помощью табл.:
А В ¬А А 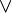 В А&B A→B A В А&B A→B A
B
0 0 I 0 0 I I
0 I I I 0 I 0
I 0 0 I 0 0 0
I I 0 I I I I
Используя эту таблицу можно получить истинностную таблицу для произвольной ПФ.
2.Алгебра высказываний; тавтологии и противоречия
Сложное высказывание, истинное при любых значениях входящих в него элементарных высказываний, называется тавтологией. Отрицание тавтологией есть противоречие. Если ПФ не является противоречием, то она наз-ся выполнимой. Из тавтологий получаются высказывания, истинные по форме, а из противоречий – высказывания, ложные по форме(а не по содержанию).
Если А – тавтология, то ¬А – противоречие. И наоборот.
Если А и А→В – тавтологии, то В – тавтология.
Если А→В и А→¬В – тавтологии, то А – противоречие.
Если в тавтологии вместо пропозициональных букв подставить произвольные ПФ, то снова получится тавтология.
3.Алгебра высказываний; логическая эквивалентность и логическое следствие
Логическая равнозначность: ЭКВИВАЛЕНТНОСТЬ - определяет результат сравнения двух простых логических выражений А и В. Результатом ЭКВИВАЛЕНТНОСТИ является новое логическое выражение, которое будет истинным тогда и только тогда, когда оба исходных выражения одновременно истинны или ложны. Обозначается символом "эквивалентности"
.
Логическое следование: ИМПЛИКАЦИЯ - связывает два простых логических выражения, из которых первое является условием (А), а второе (В)– следствием из этого условия. Результатом ИМПЛИКАЦИИ является ЛОЖЬ только тогда, когда условие А истинно, а следствие В ложно. Обозначается символом "следовательно" → и выражается словами ЕСЛИ … , ТО …
4. Алгебра высказываний; дизъюнктивная и конъюнктивная нормальные формы
Дизъюнктивной нормальной формой(ДНФ) наз-ся дизъюнкция элементарных конъюнкций. При этом допускается, что может быть всего одно дизъюнктивное слагаемое.
Теорема. Всякая истинностная функция F порождается некоторой ДНФ
Конъюнктивной нормальной формой(КНФ) наз-ся конъюнкция элементраных дизъюнкций. При этом допускается, что может быть всего один конъюнктивный сомножитель.
Теорема. Всякая истинностная функция F порождается некоторой КНФ.
5. Алгебра высказываний; полные системы функций, базис
Система пропозициональных связок наз-ся полной, если любая пропозициональная форма может быть записана с помощью связок только из этой системы. Сис-ма пропозициональных связок наз-ся независимой, если никакая из связок этой сис-мы не может быть выражена через другие связки той же сис-мы. Полная независимая сис-ма связок наз-ся базисом.
Сис-ма связок {¬,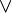 ,&} явл-ся полной. ,&} явл-ся полной.
Теорема. Система связок {¬,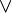 } явл-ся базисом } явл-ся базисом
6. Понятие формальной аксиоматической теории. (ФАТ)
Формальные аксиоматические теории (ФАТ) представляют собой одно из средств, используемых для решения более сложных вопросов логики, для решения которых нет эффективной процедуры. Задать ФАТ – значит определить следующие ее компоненты:
1)Алфавит теории-счетное множ-во, элементы которого служат символы для построения слов.
2) Формулы теории – те слова, которые считаются осмысленными.
3) Аксиомы теории – те формулы, которые счит-ся не нуждающимися в док-ве. Множ-во аксиом может быть бесконечным.
4) Правила вывода, определяющие, в каком случае мы считаем одну формулу непосредственным следствием других.
Если для формулы A сущ-ет вывод,то говорят, что она явл-ся теоремой ФАТ, и пишут так: � �. �.
7. Исчисление высказываний, как формальная аксиоматическая теория (ФАТ).
В кач-ве основного примера ФАТ рассмотрим исчисление высказываний (ИВ).
1)Алфавит ИВ состоит из пропозициональных букв, пропорциональных связок � � и –(не) и скобок. � и –(не) и скобок.
2) Формулы ИВ – это все ПФ, содержащие лишь связки –(не) и � � �
3)Аксиом в ИВ бесконечно много, но каждая из них пол-ся из одной из следующих 3 схем аксиом:
А1: � �; �;
A2: �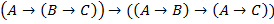 �; �;
A3: � � �
Подстановкой вместо A,B,C произвольных формул ИВ.
4) Правило вывода в ИВ всего одна: формула B счит-ся непосредственным следствием формул A и � �. (modus ponens), сокращенно MP. �. (modus ponens), сокращенно MP.
T1: � �; �;
T2: �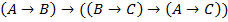 � (правило силлогизма ПС) � (правило силлогизма ПС)
T3: �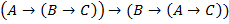 � (правило перестановки посылок ПП) � (правило перестановки посылок ПП)
T4:�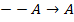 � �
T5:� � �
T6:�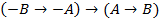 � �
T7:�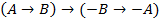 � �
T8:�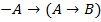 � �
T9:� � �
T10: � � �
8. Формальная аксиоматическая теория (ФАТ), определение аксиомы, правило вывода
Аксио́ма— утверждение (факт), принимаемое истинным без доказательства, а также как «фундамент» для построения доказательств.
Аксиом в ИВ бесконечно много, но каждая из них пол-ся из одной из следующих 3 схем аксиом:
А1: � �; �;
A2: �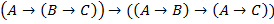 �; �;
A3: � � �
Подстановкой вместо A,B,C произвольных формул ИВ.
Правило вывода в ИВ всего одна: формула B счит-ся непосредственным следствием формул A и � �. (modus ponens), сокращенно MP. �. (modus ponens), сокращенно MP.
T1: � �; �;
T2: �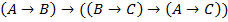 � (правило силлогизма ПС) � (правило силлогизма ПС)
T3: �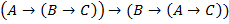 � (правило перестановки посылок ПП) � (правило перестановки посылок ПП)
T4:�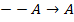 � �
T5:� � �
T6:�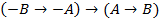 � �
T7:�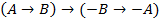 � �
T8:�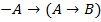 � �
T9:� � �
T10: � � �
9. Формальная аксиоматическая теория (ФАТ), формализация понятий теоремы и ее док-ва.
В ФАТ выводом или док-ом формулы A наз-ся конечная цепочка формул, каждая из которых есть либо аксиома, либо непосредственное следствие каких-либо из предыдущих формул по одному из правил вывода, причем последняя формула этой цепочки- это и есть формула A.Если для формулы A сущ-ет вывод,то говорят, что она явл-ся теоремой ФАТ, и пишут так: � �. �.
Предложение : Всякая формула, полученная по схеме �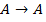 �явл-ся теоремой ИВ. �явл-ся теоремой ИВ.
Док-во: чтобы док-ть, что формула явл-ся теоремой, надо предъявить ее вывод. Вот он:
(1)�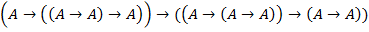 � схема� � схема�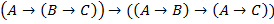 �; �;
(2)�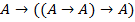 � схема � � схема � �; �;
(3)� � из (1), (2) по MP (формула B счит-ся непосредственным следствием формул A и � � из (1), (2) по MP (формула B счит-ся непосредственным следствием формул A и � �.) �.)
(4)� � схема � � схема � �; �;
(5)� � из (3), (4) по MP � из (3), (4) по MP
10. Формальная аксиоматическая теория (ФАТ),теорема дедукции, правило силлогизма и перестановки посылок.
�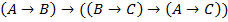 � (правило силлогизма ПС) � (правило силлогизма ПС)
�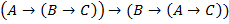 � (правило перестановки посылок ПП) � (правило перестановки посылок ПП)
Теорема дедукции: Если Г, A|-B, то Г|-A B. B.
Доказательство. Пусть последовательность формул B1, B2, …, Bm есть вывод B из Г,A. В ней Bm = B. Индукцией по i покажем, что Г|-A Bi для каждого i = 1, …, m. При i = m будем иметь утверждение теоремы. Сначала заметим, что, по определению вывода, для каждой формулы Bi при i Bi для каждого i = 1, …, m. При i = m будем иметь утверждение теоремы. Сначала заметим, что, по определению вывода, для каждой формулы Bi при i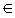 {1, …, m} возможны следующие случаи: 1) Bi =A, 2) Bi – аксиома, 3) Bi {1, …, m} возможны следующие случаи: 1) Bi =A, 2) Bi – аксиома, 3) Bi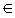 Г. В случае 1), ввиду |-A Г. В случае 1), ввиду |-A A (пример 1), имеем |-A A (пример 1), имеем |-A Bi и, следовательно, Г|-A Bi и, следовательно, Г|-A Bi. В случаях 2) и 3) выводом A Bi. В случаях 2) и 3) выводом A Bi из Г служит последовательность Bi, Bi Bi из Г служит последовательность Bi, Bi (A (A Bi), A Bi), A Bi, в которой первая формула является аксиомой или принадлежит Г, вторая формула есть аксиома 1 и третья получена из них по правилу отделения. Bi, в которой первая формула является аксиомой или принадлежит Г, вторая формула есть аксиома 1 и третья получена из них по правилу отделения.
1. A (B (B A) A)
В качестве единственного правила вывода в ИВ мы принимаем правило modus ponens, или правило отделения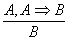 ,по которому, каковы бы ни были формулы A и B, из формул A и A ,по которому, каковы бы ни были формулы A и B, из формул A и A B получается формула B.При i ≤ 2 других случаев нет, и база индукции установлена. При i > 2 возможен еще один случай: 4) Bi получена из Bj и Bk для некоторых j, k <i по правилу отделения, Bk = (Bj B получается формула B.При i ≤ 2 других случаев нет, и база индукции установлена. При i > 2 возможен еще один случай: 4) Bi получена из Bj и Bk для некоторых j, k <i по правилу отделения, Bk = (Bj Bi) и, по предположению индукции, Г|-A Bi) и, по предположению индукции, Г|-A Bj и Г|-A Bj и Г|-A Bk, т.е. Г|-A Bk, т.е. Г|-A (Bj (Bj Bi). В этом случае вывод A Bi). В этом случае вывод A Bi из Г строится так: из Г выводится A Bi из Г строится так: из Г выводится A Bj, берется аксиома 2 в виде (A Bj, берется аксиома 2 в виде (A Bj) Bj) ((A ((A (Bj (Bj Bi)) Bi)) (A (A Bi)) и по правилу отделения Bi)) и по правилу отделения
2. (A B) B) ((A ((A (B (B C)) C)) (A (A C)) C))
В качестве единственного правила вывода в ИВ мы принимаем правило modus ponens, или правило отделения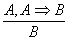 ,по которому, каковы бы ни были формулы A и B, из формул A и A ,по которому, каковы бы ни были формулы A и B, из формул A и A B получается формула B.получается формула (A B получается формула B.получается формула (A (Bj (Bj Bi)) Bi)) (A (A Bi), из Г выводится A Bi), из Г выводится A (Bj (Bj Bi) и из последних двух формул по правилу отделения получается требуемая формула A Bi) и из последних двух формул по правилу отделения получается требуемая формула A Bi. Bi.
11.Исчисление высказываний: связь между теоремами исчисления высказываний и тавтологиями.
Всякая теорема в ИВ является тавтологией.
Лемма:� �,…� �,…�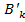 �|-A� �|-A� � (*) � (*)

Теорема:Всякая тавтология является теоремой в ИВ.
Док-во:Пусть А зависит от букв � �,…� �,…�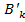 � и является тавтологией.Тогда А� � и является тавтологией.Тогда А� �=А для любого истинностного набора букв � �=А для любого истинностного набора букв � �.Следовательно по лемме(*) имеем �.Следовательно по лемме(*) имеем
� �,…� �,…�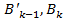 �|-A, � �|-A, � �,…� �,…� �|-A �|-A
Применив теорему дедукции получим
� �,…� �,…� �A ,� �A ,�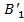 �,…� �,…� � �
Применив схему Т9�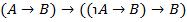 �, по правилу МР получим �, по правилу МР получим
� �,…� �,…� �|-A �|-A
Таким образом, мы смогли исключить из посылок �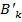 �.Повторяя рассуждения еще k-1 раз, мы можем исключить из посылок все буквы � �.Повторяя рассуждения еще k-1 раз, мы можем исключить из посылок все буквы � � и получим окончательно, что |-A.Следовательно, любая тавтология А является теоремой ИВ. � и получим окончательно, что |-A.Следовательно, любая тавтология А является теоремой ИВ.
12. Логика предикатов: понятия терма и предиката, кванторы.
Предикат – это высказывание, в которое можно подставлять аргументы. Если аргумент один – то предикат выражает свойство аргумента, если больше – то отношение между аргументами.
Пример предикатов. Возьмём высказывания: ``Сократ - человек'', ``Платон - человек''. Оба эти высказывания выражают свойство ``быть человеком''. Таким образом, мы можем рассматривать предикат ``быть человеком'' и говорить, что он выполняется для Сократа и Платона.
Функциональные буквы, применённые к предметам, порождают термы. Более точно:
предметные постоянные и предметные переменные суть термы;
если� �— функциональная буква, и t1, ..., tn — термы, то �— функциональная буква, и t1, ..., tn — термы, то
�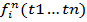 �-тоже терм. �-тоже терм.

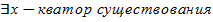
Квантор всеобщности — это условие, которое верно для всех обозначенных элементов, в отличие от квантора существования, где условие верно только для каких-то отдельных из указанных чисел.
Выражение 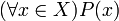 читается так: читается так:
для любого (всякого, каждого) [значения] x из X P(x) [истинно];
всякий (любой, каждый) элемент x множества X (где X — множество значений переменной x) обладает свойством P(x);
каково бы ни было x, P(x) истинно.
квантор существования — это предикат свойства или отношения для, по крайней мере, одного элемента области определения.
Выражение 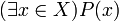 читается так: читается так:
существует [значение] x из X такое, что P(x) [истинно]
для некоторых [значений] x из X, P(x) [истинно]
существует элемент x множества X, обладающий свойством P(x)
по крайней мере (хотя бы) один элемент x множества X обладает свойством P(x)
некоторые элементы множества X обладает свойством P(x)
найдётся такое x из X, что P(x) истинно
13. Логика предикатов: логическая общезначимость.
Если формула логики предикатов истинна при любой её интерпретации при любых значениях переменных, то эта формула называется логически общезначимой. 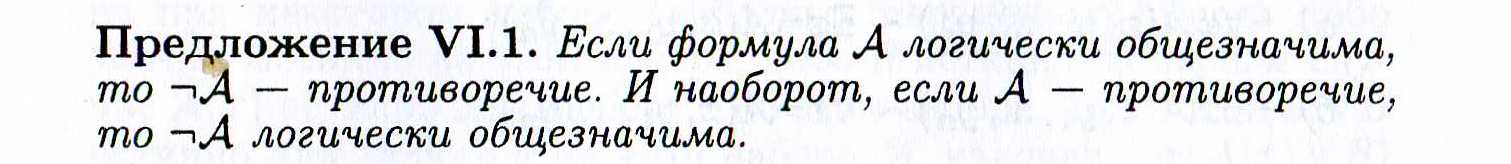
14. Логика предикатов: эквивалентность формул логики предикатов.
  
15. Логика предикатов: нормальные.
Теорема Для любой формулы логики предикатов существует логически эквивалентная ей нормальная пренексная формула.

16 теория алгоритмов. Нормальные алгорифмы Маркова.
Путь имеется некоторый алфавит А (т.е. конечное множество, эл-ты которого буквы).Конечные последовательности этих букв образуют слова (пустое слово- Λ). Длиной слова Р –количество букв в нем-|Р|. Слова Р=а1,а2..аn и Q=b1,b2…bn, то запись PQ=a1,a2…anb1?b2…bn и называется конкатенацией слов P и Q.
Пусть заданы некоторый алфавит А(. и → не являются буквами алфавита). Если P и Q-слова в алфавите А,то записи Р→ Q и Р→ .Q называются простой и заключительной формулами подстановки. Конечный список формул вида Р1→(.) Q1
Р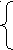 2→(.) Q2 2→(.) Q2
………….
Рn→(.) Qn Называется схемой нормального алгоритма. Детерминированный процесс переработки слов алфавита А, определяемый этой схемой, называется нормальным алгорифмом Маркова в алфавите А:
Пусть имеется слово S. Просматривая сверху вниз формулы схемы алгорифма, находим первую из них Pk→ (.)Qk такую,что Pk является подсловом слова S. Пусть R1PkR2-самое левое вхождение слова Pk слово S.Заменяем в этом вхождении слово Pk на слово Qk и получаем слово R1QkR2,которое обозначим S1. Если при этом используемая формула подстановки была заключительной, то работа алгорифма завершается, и S1 считается результатом применения нормального алгорифма к слову S. Если же формула подстановки простая, укзанная процедура повторяется для слова S1 и так далее. Таким образом,начальное слово S последовательно перерабатывается в слова S1,S2,S3… если описанный процесс заканчивается словом Sk, то Sk считается результатом обработки слова S нормальным алгорифмом. Если процесс никогда не закончится,то он не применим в данном случае.
Нормальный алгорифм над алфавитом А – в формулах подстановки допустимо использовать слова из некоторого расширения алфавита А(слова, в записи которых используются дополнительные буквы).
Принцип нормализации – для любого алгоритма,перерабатывающего слова алфавита А, может быть построен эквивалентный ему нормальный алгоритм над алфавитом А.
17.теория алгоритмов. Интуитивное понятие алгоритма.
Понятие алгоритма в общем виде невозможно строго определить, поскольку оно не сводится к другим, уже определенным понятиям. Овладевать подобными понятиями приходится интуитивно, пользуясь нестрогими разъяснениями. Так под алгоритмом понимается предписание, которое абсолютно четко и однозначно определяет некоторый вычислительный процесс.Этот процесс получает исходные данные, начинает их перерабатывать, и в зависимости от этих данных либо останавливается, выдав результат, либо останавливается без результата, либо не останавливается(в посл. 2х случаях алгоритм неприменим к данным).Примеры: сложение, вычитание, умножение, деление. Интуитивного понимания термина «алгоритм» бывает достаточно, чтобы решить, является ли какое-то предписание алгоритмом.
18.теория алгоритмов. Нормальные алгорифмы Маркова,как уточнение понятия алгоритма.
Однако понятно, что интуитивного определения недостаточно для того, чтобы доказать, что для решения той или иной задачи алгоритма не сущ-ет (а такие алгоритмически неразрешимые задачи в мат-ке есть).Утверждения такого рода могут быть доказаны только в рамках какого-то уточнения понятия алгоритма. Основные варианты таких уточнений- машина Поста, машина Тьюринга и нормальные алгоритмы Маркова, предложенные Марковым в 1947г.
19. Теория алгоритмов. Машина Поста.
Машина Поста (МП) — абстрактная вычислительная машина, предложенная Эмилем Постом которая отличается от машины Тьюринга большей простотой. Обе машины «эквивалентны» и были созданы для уточнения понятия «алгоритм»
МП состоит из каретки (или считывающей и записывающей головки) и разбитой на секции бесконечной в обе стороны ленты (см. пример ниже). Каждая секция ленты может быть либо пустой — 0, либо помеченной меткой 1. За один шаг каретка может сдвинуться на одну позицию влево или вправо, считать, поставить или уничтожить символ в том месте, где она стоит. Работа МП определяется программой, состоящей из конечного числа строк. Всего команд шесть:N. → J сдвиг вправо
N. ← J сдвиг влево
N. 1 J запись метки
N. 0 J удаление метки
N. ? J1, J0 условный переход по метке
N. Stop остановка, где N. — номер строки, J — строка на которую переходит управление далее.
Для работы машины нужно задать программу и ее начальное состояние (т. е. состояние ленты и позицию каретки). После запуска возможны варианты:1.работа может закончиться невыполнимой командой (стирание несуществующей метки или запись в помеченное поле);2. работа может закончиться командой Stop;3.работа никогда не закончится.
20 Теория алгоритмов. Машина Тьюринга.
Маши́на Тью́ринга (МТ) — абстрактный исполнитель (абстрактная вычислительная машина). В состав машины Тьюринга входит бесконечная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент), разделённая на ячейки, и управляющее устройство, способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки ленты символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма.Машина Тьюринга называется детерминированной, если каждой комбинации состояния и ленточного символа в таблице соответствует не более одного правила. Если существует пара «ленточный символ — состояние», для которой существует 2 и более команд, такая машина Тьюринга называется недетерминированной.
21. Исчисление высказываний. Построение доказательства Методом Modus ponens
Одним из возможных вариантов (Гильбертовской) аксиоматизации логики высказываний является следующая система аксиом:
 ; ;
 ; ;
 ; ;
 ; ;
 ; ;
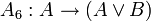 ; ;
 ; ;
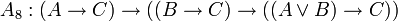 ; ;
 ; ;
 ; ;
 . .
вместе с единственным правилом:
Modus ponens (правило заключений): если A и A→B — выводимые формулы, то B также выводима.
Форма записи: 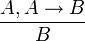 , где A, B — любые формулы. , где A, B — любые формулы.
Принцип работы правил вывода хорошо иллюстрирует следующий пример:
«Если известно, что высказывание «А» влечет (имплицирует) высказывание «В», а также известно, что высказывание «А» истинно, то, следовательно, «В» истинно»
22. Исчисление высказываний. Построение доказательства методом резолюций
В математической логике и автоматическом доказательстве теорем, правило резолюций – это правило вывода, восходящее к методу доказательства теорем через поиск противоречий; используется в логике высказываний и логике предикатов первого порядка. Правило резолюций, применяемое последовательно для списка резольвент, позволяет ответить на вопрос, существует ли в исходном множестве логических выражений противоречие. Правило разработано Джоном Аланом Робинсоном в 1965.Пусть C1 и C2 - два предложения в исчислении высказываний, и пусть 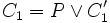 , а , а 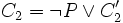 , где P - пропозициональная переменная, а C'1 и C'2 - любые предложения (в частности, может быть, пустые или состоящие только из одного литерала). , где P - пропозициональная переменная, а C'1 и C'2 - любые предложения (в частности, может быть, пустые или состоящие только из одного литерала).
Правило вывода 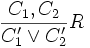 называется правилом резолюции. называется правилом резолюции.
Предложения C1 и C2 называются резольвируемыми (или родительскими), предложение  - резольвентой, а формулы P и - резольвентой, а формулы P и 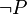 - контрарными литералами. - контрарными литералами.
23. Исчисление высказываний. Построение доказательства методом Вонга
Близким к методу резолюций является метод Вонга, в котором тоже используется сконструированная конъюнктивно-дизъюнктивная нормальная форма представления исходной клаузы, а аксиому порядка заменяет клауза Вонга:
X, L X; R,
здесь X пробегает некоторые буквы, входящие в клаузу, а L и R — определенные комбинации дизъюнктов и конъюнктов.
Конструктивная процедура доказательства сводится к последовательной разбивке дизъюнктов или конъюнктов таким образом, чтобы слева и справа от метаимпликации появилась одна и та же буква X. Если в результате такой разбивки все конечные клаузы приобретают вид клаузы Вонга, то и исходная клауза была составлена верно. Разберем метод Вонга на примере доказательства справедливости правила отделения:
А, А → В В или А, А В В.
Здесь имеется только один дизъюнкт, который можно разбить на две новых клаузы:
А, А В и А, В В.
Вторая клауза удовлетворяет и аксиоме порядка и клаузе Вонга. В качестве Х в ней выступает терм В, L = А и R = 0. Первая же клауза тоже будет удовлетворять необходимым требованиям, но только после того, как терм А из левой части клаузы с противоположным знаком перенести в правую часть. Тогда будем иметь:
А А; В где Х = А, L = 1 и R = В.
При большом числе термов в исходной клаузе прибегают к специальной нумерации производных клауз, чтобы не запутаться. Пусть требуется установить справедливость следующей клаузы:
X Y, (X → Y) U, Z → (Y → W) (W → X) → (Z X).
Приведем ее в соответствующую конъюнктивно-дизъюнктивную нормальную форму:
X Y, X Y U, Z Y W W X; Z; X.
Далее разобьем первый дизъюнкт, в результате получим две производные клаузы:
1. X, X Y U, Z Y W W X; Z; X ,
2. Y, X Y U, Z Y W W X; Z; X .
Клауза (1) отбрасывается, так как она удовлетворяет клаузе Вонга. Разбивая дизъюнкт клаузы (2), получаем еще три клаузы:
2.1. Y, X, Z Y W W X; Z; X,
2.2. Y, Y, Z Y W W X; Z; X,
2.3. Y, U, Z Y W W X; Z; X.
Клаузы (2.1) и (2.2) сводятся к одной клаузе —
2.1. Y, Z Y W W X; Z; X.
Разобьем ее:
2.1.1. Y, Z W X; Z; X,
2.1.2. Y, Y W X; Z; X,
2.1.3. Y, W W X; Z; X.
Первые две клаузы удовлетворяют клаузе Вонга. У клаузы (2.1.3) нужно разбивать конъюнкт:
2.1.3.1. Y, W W; Z; X,
2.1.3.2. Y, W X; Z; X.
Теперь обе клаузы имеют вид клаузы Вонга.
Но у нас осталась еще ветвь (2.3). Она отличается от рассмотренной ветви (2.1) наичием непарного терма U, который, однако, не может повлиять на конечный результат, т.е. разбиение клаузы (2.3) практически полностью совпадает с разбиением клаузы (2.1). Следовательно, исходная клауза была записана верно.
24. Исчисление высказываний. Перенос высказываний через знак выводимости
знак выводимости
Теорема дедукции
Пусть А и В – формулы исчисления высказываний. Тогда если АВ, то АВ
или
Пусть А и В – формулы исчисления высказываний, Г – множество формул исчисления высказываний, тогда если Г,А В, то Г АВ
Например,
АВ,ВС,АС применим теорему дедукции
АВ,ВСАС применим теорему дедукции
АВ(ВС)(АС) применим теорему дедукции
(АВ)(ВС)(АС) |
|
|
 Скачать 1.21 Mb.
Скачать 1.21 Mb.





 2→(.) Q2
2→(.) Q2