Билет 2. 1 Числовым рядом называется бесконечная сумма чисел
 Скачать 87.49 Kb. Скачать 87.49 Kb.
|
|
Билет 2 1)Числовым рядом называется бесконечная сумма чисел 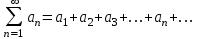 Числа 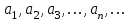 называются членами ряда, а число называются членами ряда, а число 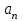 ‒ общим членом ряда. ‒ общим членом ряда. Суммы вида 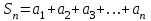 называются частичными суммами ряда. называются частичными суммами ряда. Числовой ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм: 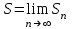 , ,который называется суммой ряда. В противном случае, если 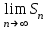 не существует или равен бесконечности, то числовой ряда называется расходящимся и суммы не имеет. не существует или равен бесконечности, то числовой ряда называется расходящимся и суммы не имеет.Необходимый признак сходимости: Если ряд 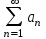 сходится, то сходится, то 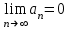 . .Следствие: если 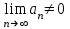 , то ряд , то ряд 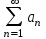 расходится. расходится.Достаточные признаки сходимости: 1-й признак сравнения Пусть 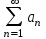 и и 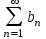 ‒ ряды с положительными членами, причем ‒ ряды с положительными членами, причем 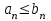 для всех номеров для всех номеров 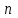 , начиная с некоторого. Тогда: , начиная с некоторого. Тогда:1) если ряд 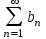 сходится, то сходится и ряд сходится, то сходится и ряд 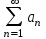 ; ;2) если ряд 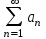 расходится, то расходится и ряд расходится, то расходится и ряд 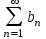 . .2-й признак сравнения Пусть 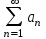 и и 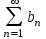 ‒ ряды с положительными членами, причем существует конечный и отличный от нуля предел ‒ ряды с положительными членами, причем существует конечный и отличный от нуля предел 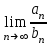 . Тогда ряды . Тогда ряды 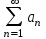 и и 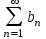 сходятся или расходятся одновременно. сходятся или расходятся одновременно.При использовании признаков сравнения, как правило, сравнивают исходный ряд: а) с соответствующим рядом Дирихле 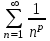 , где , где 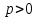 . Этот ряд сходится при . Этот ряд сходится при 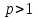 и расходится при и расходится при 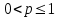 . Частным случаем ряда Дирихле (при . Частным случаем ряда Дирихле (при 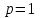 ) является гармонический ряд ) является гармонический ряд 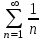 , который расходится. При сравнении часто используют эквивалентность следующих бесконечно малых последовательностей (при , который расходится. При сравнении часто используют эквивалентность следующих бесконечно малых последовательностей (при 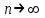 ): ):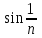 ̴ ̴ 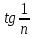 ̴ ̴ 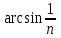 ̴ ̴ 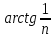 ̴ ̴ 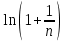 ̴ ̴ 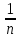 . .б) с геометрическим рядом 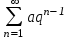 , составленным из членов бесконечной геометрической прогрессии со знаменателем , составленным из членов бесконечной геометрической прогрессии со знаменателем 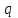 и первым членом и первым членом 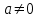 . Если . Если 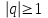 , то геометрический ряд расходится, если , то геометрический ряд расходится, если 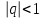 ‒ сходится, причем его сумма находится по формуле ‒ сходится, причем его сумма находится по формуле 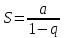 . .Признак Даламбера Пусть 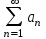 ‒ ряд с положительными членами, и существует конечный предел ‒ ряд с положительными членами, и существует конечный предел 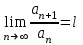 . Тогда, если . Тогда, если 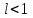 , то данный ряд сходится; если же , то данный ряд сходится; если же 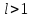 , то ‒ расходится. Если , то ‒ расходится. Если 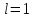 , то ряд может сходиться или расходиться; в этом случае требуется исследовать ряд с помощью других методов. , то ряд может сходиться или расходиться; в этом случае требуется исследовать ряд с помощью других методов.Признак Коши Пусть 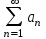 ‒ ряд с положительными членами, и существует конечный предел ‒ ряд с положительными членами, и существует конечный предел 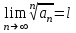 . Тогда, если . Тогда, если 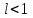 , то данный ряд сходится; если же , то данный ряд сходится; если же 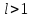 , то ‒ расходится. Если , то ‒ расходится. Если 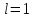 , то ряд может сходиться или расходиться; в этом случае требуется исследовать ряд с помощью других методов. , то ряд может сходиться или расходиться; в этом случае требуется исследовать ряд с помощью других методов.Интегральный признак сходимости Пусть 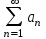 ‒ ряд с положительными членами, для которого существует положительная, непрерывная и монотонно убывающая на промежутке ‒ ряд с положительными членами, для которого существует положительная, непрерывная и монотонно убывающая на промежутке 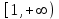 функция функция 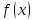 такая, что такая, что 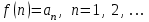 Тогда ряд 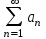 и несобственный интеграл и несобственный интеграл 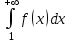 сходятся или расходятся одновременно. сходятся или расходятся одновременно.2) 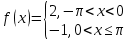 Ряд Фурье имеет вид: где  Итак,  3) Представить заданную функцию w=f(z), где z=x+iy, в виде w=u(x;y)+iv(x;y) и проверить, является ли она аналитической. Если да, то найти значение ее производной в точке 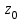 . .f(z)=2z2-z+i, z0=1+i Решение. f(z)=2(x+iy)2-(x+iy)+i=2x2+4xiy-2y2-x-iy+i u(x,y)=2x2-2y2-x v(x,y)=4xy-y+1 Функция является аналитической, то выполняются условия Коши – Римана: 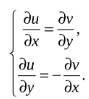 Вычислим частные производные, du/dx=4x-1 dv/dy=4x-1 du/dy=-4y dv/dx=4y du/dx =dv/dy du/dy =-dv/dx условие Коши-Римона выполняется. Функция является аналитической, Вычислим производную в точке zo=2-i. w'(z)=4z-1 w'(2i) =3+4i |
