333184 заказ. 1. Метрологические характеристики средств измерений

• Название: 1. Метрологические характеристики средств измерений
• Дата: 13.12.2022
• Размер: 249.79 Kb.
• Имя файла: 333184 заказ.docx
• Тип: Документы; #842316

1.Метрологические характеристики средств измерений

Важнейшими свойствами средств измерений явля­ются те, от которых зависит качество получаемой с их помощью измерительной информации. Качество измерения характеризуется точностью, достоверностью, правильностью, сходимостью и воспроизводимостью измерений, а также размером допускаемых погрешностей.

Метрологические характеристики (свойства) средств — это такие характеристики, которые предназначены для оценки технического уровня и качества средства измерения, для определения результатов измерения и расчетной оценки характеристик инструментальной составляющей погрешности измерения.

ГОСТ 8.009—84 устанавливает комплекс нормируемых метрологических характеристик средств измерения, который выбирается из числа приводимых ниже.

Характеристики, предназначенные для определения результатов измерения (без введения поправки):

функция преобразования измерительного преобразователя,

значение однозначной или многозначной меры;

цена деления шкалы измерительного прибора или многозначной меры;

вид выходного кода, число разрядов кода.

Характеристики погрешностей средств измерения — характеристики систематической и случайной составляющих погрешностей, вариация выходного сигнала средств измерения либо характерис­тика погрешности средств измерения.

Характеристики чувствительности средств измерения к влияю­щим величинам — функция влияния или изменение значений мет­рологических характеристик средств измерения, вызванные изме­нениями влияющих величин в установленных пределах.

Динамические характеристики средств измерения подразделяют на полные и частные. К полным динамическим характеристикам относят: переходную, амплитудно-фазовую и импульсную харак­теристики, передаточную функцию, к частным — время реакции, коэффициент демпфирования, постоянную времени, значение резонансной собственной круговой частоты.

Неинформативные параметры выходного сигнала средств измере­ния — параметры выходного сигнала, не используемые для пере­дачи или индикации значения информативного параметра вход­ного сигнала измерительного преобразователя или не являющиеся выходной величиной меры.

Рассмотрим более подробно наиболее часто встречающиеся мет­рологические показатели средств измерения.

Цена деления шкалы — это разность значений величин, соот­ветствующих двум соседним отметкам шкалы. Например, если пе­ремещение указателя шкалы из положения I в положение II (рис. 1.13, а) соответствует изменению величины в 0,001 мм, то цена деления этой шкалы равна 0,001 мм. Значения цен делений выбирают из ряда 1, 2, 5, 10, 20, 50, 100, 200, 500 мкм. Но чаще всего используют кратные и дольные значения от 1 до 2, а именно: 0,01; 0,02; 0,1; 0,2; 1; 2; 10 мкм и т. д. В угломерных средствах измерения применяются круговые шкалы с ценой деления 1, а дополнительное отсчетное устройство позволяет отсчитывать доли этих делений в минутах и секундах. Цена деления шкалы всегда указывается на шкале средства измерений.

Интервал деления шкалы — это расстояние между серединами двух соседних штрихов шкалы (рис. 1 б). На практике исходя из разрешающей силы глаз оператора (остроты зрения) с учетом ши­рины штрихов и указателя минимальный интервал деления шка­лы принимают равным 1 мм, а максимальный — 2,5 мм. Наиболее распространенной величиной интервала является 1 мм. У пневматических приборов с водяным манометром интервал деления шкалы составляет около 5 мм.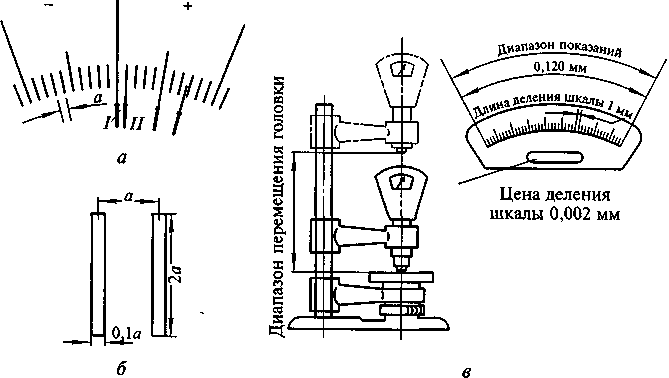


Рис. 1.. Основные метрологические характеристики средств измерения

Начальное и конечное значения шкалы — соответственно наимень­шее и наибольшее значения измеряемой величины (рис. 1 в), указанные на шкале, характеризующие возможности шкалы средств измерения и определяющие диапазон показаний.

Диапазон показаний — область значений шкалы, ограниченная начальным и конечным значениями шкалы (см. рис.1, в). Эту характеристику часто называют пределами измерения по шкале. Например, для индикаторов часового типа диапазон может составлять 2,5или 10 мм, для гладких микрометров — 25 мм, для оптиметра — ±0,1 мм.

Диапазон измерения, который часто называют пределом измере­ния средства измерения, — это диапазон значений измеряемой ве­личины, который может быть измерен данным средством измерения и для которого нормируется допускаемая погрешность средства измерения.

Одной из основных характеристик средств измерения линейных и угловых величин контактным методом является измерительное усилие, которое возникает в зоне контакта измерительного наконечни­ка средства измерения с измеряемой поверхностью в направлении линии измерения. Оно необходимо для того, чтобы обеспечить ус­тойчивое замыкание измерительной цепи. В зависимости от допуска контролируемого изделия (2... 10 мкм) рекомендуемые величины измерительного усилия находятся в пределах 2,5...3,9 Н, а свыше 10 мкм — 9,8 Н. Важным показателем измерительного усилия является его перепад (колебание) — разность измерительного усилия при двух положениях указателя в пределах диапазона показаний.

Свойство средства измерения, заключающееся в его способности реагировать на изменения измеряемой величины, называется чувствительностью. Она оценивается отношением изменения положения указателя относительно шкалы к соответствующему изменению измеряемой величины.

Если измеряемой величиной является длина или угол и значение чувствительности выражается безразмерным числом, то последнее называется передаточным отношением:

i = а/с,

где а — интервал деления шкалы; с — цена деления.

Например, при цене деления индикатора 0,01 мм и интервале деления шкалы 1,5 мм передаточное отношение будет равно 150.

Порог чувствительности средства измерения — изменение измеряемой величины, вызывающее наименьшее изменение его показаний, обнаруживаемое при нормальном способе отсчета. Эта характеристика важна при оценке малых перемещений.

Вариация показаний — наибольшая экспериментально определяемая разность между повторными показаниями средства измерения, соответствующими одному и тому же действительному значению измеряемой величины при неизменных внешних условиях. Обычно вариация показаний у средств измерения составляет 10... 50 % от цены деления, она определяется путем многократного арретирования наконечника средства измерения.

Погрешность измерения — это отклонение  результата измерения Х_изм от действительного значения Q_Д измеряемой величины:  = Х_изм  Q_Д. Тогда погрешность средства измерения _п — это разность между показанием прибора Х_п и действительным значением измеряемой величины:

 = Х_п  Q_Д.

Наряду с терминами «погрешность измерения», «погрешность средства измерения» используется понятие «точность измерения», которое отражает близость его результатов к истинному значению измеряемой величины. Высокая точность измерения соответствует малым погрешностям измерения. Погрешности измерения обычно классифицируют по причине их возникновения и по виду погрешностей.

Инструментальные погрешности возникают вследствие недостаточно высокого качества элементов средств измерения и контроля. К этим погрешностям можно отнести погрешности изготовления и сборки СИ; погрешности из-за трения в механизме СИ, недостаточной жесткости его деталей и т.п. Инструментальная погрешность индивидуальна для каждого СИ.

Причиной возникновения методических погрешностей служит несовершенство метода измерения, т.е. то, что мы сознательно измеряем, преобразуем или используем на выходе средств измерения не ту величину, которая нам нужна, а другую, которая отражает нужную лишь приблизительно.

Основная и дополнительная погрешности. За основную погрешность принимают погрешность средства измерения, используемого в нормальных условиях, оговоренных в нормативно-технических документах (НТД). Известно, что наряду с чувствительностью к измеряемой величине средство измерения имеет некоторую чувствительность и к неизмеряемым, но оказывающим влияние величинам, например температуре, атмосферному давлению, вибрации, ударам и т.д. Поэтому любое средство измерения имеет основную погрешность, которая отражается в НТД.

При эксплуатации средств измерения и контроля в производственных условиях возникают значительные отклонения от нормальных условий, вызывающие дополнительные погрешности. Эти погрешности нормируются соответствующими коэффициентами влияния изменения отдельных влияющих величин на изменение показании в виде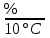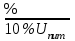

; ; и т.д.

Погрешности средств измерения нормируют установлением предела допускаемой погрешности. Предел допускаемой погрешности средства измерения — наибольшая (без учета знака) погрешность средства измерения, при которой оно может быть признано и допущено к применению. Например, пределы допускаемой погрешности 100-мм концевой меры длины класса 1 составляют ±50 мкм, а для амперметра класса 1,0 составляют ± 1 % от верхнего предела измерений.

Погрешности средств измерения могут выражаться:

в виде абсолютной погрешности :

для меры

 = Х_н - Х_Д,

где Х_н — номинальное значение; Х_Д — действительное значение измеряемой величины;

для прибора

 = Х_п  Х_Д,

где Х_п — показание прибора;

в виде относительной погрешности (100%):

 = (/Х_Д)100,

в виде приведенной погрешности (100%):

= (/X_N)100,

где X_N — нормирующее значение измеряемой физической величины.

В качестве нормирующего значения может быть принят предел измерения данным СИ. Например, для весов с пределом измерения массы 10 кг X_N = 10 кг.

Если в качестве нормирующей величины принимается размах всей шкалы, то именно к значению этого размаха в единицах измеряемой физической величины и относят абсолютную погрешность. Например, для амперметра с пределами -100...+100 мА X_N = 200 мА.

Если в качестве нормирующей величины принимается длина шкалы прибора, равная единице, то X_N = 1.

На каждое СИ погрешность приводится только в какой-то од­ной форме.

Если погрешность СИ при неизменных внешних условиях постоянна во всем диапазоне измерений, то

 = ±а. (4)

Если она меняется в указанном диапазоне, то

 = ±(а + bx). (5)

При  = ± а погрешность называется аддитивной, а при  = ±(а+bx) — мультипликативной.

Для аддитивной погрешности

 = ± р. (6)

Для мультипликативной погрешности

. (7)

Приведенная погрешность

 = ± q.

Значения р, с, d, q выбираются из ряда чисел: 110ⁿ; 1,510ⁿ; 1,610ⁿ; 210ⁿ; 2,510ⁿ; 310ⁿ; 410ⁿ; 510ⁿ; 610ⁿ, где n — положительное или отрицательное целое число, включая нуль.

Для обобщенной характеристики точности средств измерения, определяемой пределами допускаемых погрешностей (основной и дополнительной), а также другими их свойствами, влияющими на погрешность измерений, вводится понятие «класс точности средств измерения». Единые правила установления пределов допускаемых погрешностей показаний по классам точности средств измерения регламентирует ГОСТ 8.401—80. Классы точности удобны для сравнительной оценки качества средств измерения, их выбора, международной торговли.

Классы точности определяются стандартами и техническими условиями, содержащими технические требования к средствам измерения. Для каждого класса точности средства измерения конкретного типа устанавливаются конкретные требования к метрологическим характеристикам, в совокупности отражающие уровень точности. Единые характеристики для средств измерения всех классов точности (например, входные и выходные сопротивления) нормируются независимо от класса точности. Средства измерения нескольких физических величин или с несколькими диапазонами измерений могут иметь два и более классов точности. Например, электроизме­рительному прибору, предназначенному для измерения электриче­ского напряжения и сопротивления, могут быть присвоены два класса точности: один — как вольтметру, другой — как амперметру.

Классы точности присваивают средствам измерения при разработке. В процессе эксплуатации метрологические характеристики средств измерения ухудшаются. Поэтому допускается понижение класса их точности по результатам метрологической аттестации.

В связи с большим разнообразием средств измерения и их метрологических характеристик ГОСТ 8.401—80 определены способы обозначения, причем выбор того или иного способа зависит от того, в каком виде нормирована погрешность. Для СИ, у которых погрешность измерения определяется в соответствии с формулами (4) и (5), класс точности присваивается порядковым номером, начиная для самого точного с 1 и далее по мере возрастания погрешности.

Если погрешность определяется по формулам (6) или (7), класс точности СИ соответствует значениям относительной или приведенной погрешности, выраженной в %.

Например, если  = ± 1 %, то класс точности СИ — 0,1; если при­веденная погрешность  = ± 1,5 %, то класс точности СИ — 1,5. Это справедливо для приведенной погрешности, нормируемой значением физической величины в принятых единицах. В тех случаях, когда погрешность нормируется длиной шкалы прибора 1, класс точно­сти также равен численному значению у, но обозначается по-другому. Например, при  = 0,5 % (X_N = 1) класс точности — 0,5.

Если погрешность СИ определяется формулой (7) (мультипликативная погрешность), то она обозначается c/d. Если



то класс точности СИ обознается 0,02/0,01.

2.Методики выполнения измерений

В соответствии с Законом «Об обеспечении единства измерений» измерения должны проводиться по методикам, аттестованным в установленном порядке.

Методика выполнения измерений — это совокупность операций и правил, выполнение которых обеспечивает получение результатов с известной погрешностью.

Поскольку погрешность определяется не только метрологическими характеристиками средств измерений, но и погрешностью отбора и приготовления проб, условиями проведения измерений, ошибкой оператора и другими причинами, это определение означает, что методики выполнения измерений могут разрабатываться и быть аттестованными только применительно к конкретным условиям проведения измерения с использованием конкретных средств.

Данное утверждение не означает, что для каждой измерительной или испытательной лаборатории должны разрабатываться собственные методики. Но если лаборатория использует тип средства измерения, приведенный в аттестованной методике, влияющие факторы (температура и влажность окружающего воздуха и измеряемой среды, напряжение и частота электрической сети, вибрация, внешнее магнитное поле и др.) находятся в определенном данной методикой диапазоне, а оператор соответствует установленной в ней квалификации, то физические величины будут измеряться в этой лаборатории с известной погрешностью.

Методики выполнения измерений содержат следующие структурные элементы и разделы:

наименование;

область применения;

нормативные ссылки;

определения;

обозначения и сокращения;

требования к погрешности измерений или приписанные характеристики погрешности измерений;

средства измерения и вспомогательные устройства;

методы измерений;

требования безопасности, охраны окружающей среды;

требования к квалификации операторов;

условия измерений;

подготовка к выполнению измерений;

выполнение измерений;

обработка результатов измерений;

контроль точности результатов измерений;

приложения.

Порядок разработки и аттестации методик выполнения измерений определяет Росстандарт. Аттестацию методик в сферах распространения государственного метрологического контроля и надзора осуществляют ГНМЦ, территориальные органы Государственной метрологической службы и другие организации, аккредитованные на право проведения аттестации. Аттестацию методик, применяемых вне сфер распространения государственного метрологического контроля и надзора, предприятия проводят в установленном ими порядке.

Разработка методики измерений

Методика выполнения измерений (МВИ) представляет собой план прописанных действий, необходимых для получения результатов измерения по установленным показателям точности.  Измерительные работы, относящиеся к сфере госрегулирования обеспечения единства СИ, необходимо проводить по методикам, которые аттестованы установленным порядком (согласно ФЗ N 102 «Об обеспечении единства измерений»). Исключение составляют только методики, которые нужны для осуществления прямых измерений, проводимые с использованием СИ утвержденного типа, прошедших соответствующую поверку.  Итоговые данные измерений отражаются в единицах величин, разрешенных к применению на территории России.  Методики делятся на группы в зависимости от приемов получения результатов измерений: 

прямые методы измерений – это вид измерения, при осуществлении которого искомое значение величины получают из опытных данных;

косвенные методы измерений – тип измерения, итоговое значение  которого определяется, учитывая прямые измерения величин, которые связаны известной зависимостью с измеряемой величиной. Измерения данного виды применяют в тех случаях, когда нельзя использовать прямые методы измерений (пример – в случае, когда вычисляется плотность твердого тела, по результатам измерений массы и объема).  

Методики измерений можно также разделить по условиям, в которых проводятся измерения: 

контактный метод – базируется на приведение в контакт чувствительного элемента прибора с объектом измерений (пример – определение с помощью термометра температуры тела);

бесконтактный метод - основан на отсутствие  контакта между чувствительным элементом прибора и объектом измерения (пример – определение температуры пирометром в доменной печи, вычисление расстояния до объекта с помощью радиолокатора).

Типы методик измерений в соответствии с выбранным способом сравнения величины, подлежащей измерению,  с единицей:

непосредственная оценка – значения величины определяются непосредственно по отсчетному устройству, которое показывает СИ (вольтомметр, термометр и другие). Отражающая единицу измерения мера в процессе измерения не принимает участие. Эту роль в СИ выполняет шкала, она должна быть проградуирована при производстве, при использовании точных СИ;

сравнение с мерой - измеряемая величина сравнивается с величиной, воспроизводимой мерой (пример – вычисление массы на рычажных весах при помощи уравновешивания гирь).

Стоит отметить, что метод сравнения с мерой, в свою очередь, делить натри подтипа: 

нулевой – метод сравнения, при выполнении которого  доводят до нуля результирующий эффект воздействия величин на прибор сравнения (пример – определения силы электрического сопротивления мостом при помощи его полного уравновешивания);

метод замещения – основанный на сравнении с мерой, измеряемые величина замещается величиной известной, которая воспроизводится мерой, при этом сохраняются неизменными все условия (пример – процедура взвешивания с помощью поочередного перемещения измеряемой массы и гирь на одну и ту же чашу весов);

метод совпадений – разность, которую имеют значения искомая и воспроизводимая меры величин измеряются при использовании совпадения отметок шкал либо периодических сигналов (пример – наблюдение совпадений меток на шкалах штангенциркуля и нониуса).

Структура методики выполнения измерений содержат элементы и разделы:

 наименование методики;

область применения методики;

ссылки на нормативные документы;

определения;

обозначения и сокращения (в случае наличия в тексте);

требования к погрешности измерений либо приписанные характеристики погрешности измерений;

применяемые СИ и вспомогательные устройства;

методы измерений;

необходимые требования по безопасности, требования к охране окружающей среды;

требования, предъявляемые к уровню квалификации операторов;

условия проводимых измерений;

необходимая подготовка к процедуре измерений;

выполнение измерительных работ;

конечная обработка итогов измерений;

контроль точности итоговых результатов измерений;

необходимые приложения.

Порядок по разработке и процедуре аттестации методик измерений определен Федеральным агентством по техническому регулированию и метрологии.

3.Задача

Суммируя значения ранжированного вариационного ряда, определяем выборочное среднее

 =   =45.3 мм.

В графе 3 приведены разности между каждой составляющей выборки   и выборочным средним   , а в графе 4 их квадраты. Суммируя их найдем дисперсию выборки

 =   =1.269.

Для оценки рассеивания случайной величины относительно математического ожидания используются следующие характеристики: среднее квадратичное отклонение, коэффициент вариации, показатель точности и доверительный интервал.

Выборочное среднее квадратическое отклонение определяем по формуле

 =   =1.127.

Среднее квадратическое отклонение сводного результата определяем по формуле

 =   =0.252.

Выборочный коэффициент вариации определяем по формуле

 =   ∙100%=2.487%.

Коэффициент вариации показывает, как велико рассеивание результатов в сравнении со средним значением.

Показатель точности определяем по формуле

 =   ∙100%=0.556%.

Показатель точности свидетельствует о точности методики, по которой проводились испытания и получены результаты.

Доверительный интервал выборочных характеристик можно определить при помощи критерия Стьюдента по формуле

 -   ∙           +   ∙   ,

где   - критерий Стьюдента для уровня доверительной вероятности   , обычно принимаемой равной 0.95 или 0.99, и числа степеней свободы   =n-1 принимают по статистическим таблицам. Они имеются практически в каждом руководстве по математической статистике. В нашем случае:

dns-shop.ru реклама Подробнее

gazprombank.ru реклама Узнать больше Ставка до 10% годовых!

а) при   =0.95 и   =20-1=19 получим 45.3-2.095∙0.252       45.3+2.095∙0.252 и после вычислений 44.77 мм       45.83 мм,

б) при   =0.99 и   =20-1=19 получим 45.3-2.859∙0.252       45.3+2.859∙0.252 и после вычислений 44.58 мм       46.02 мм.

То есть с увеличением уровня доверительной вероятности   доверительный интервал расширяется (45.83-44.77=1.06 мм и 46.02-44.58=1.44 мм).

Проверим теперь принадлежность первого и последнего результатов испытаний (ранжированного вариационного ряда) той же генеральной совокупности, как и остальные 18 результатов. Так как выборка имеет малый объем (n=20), то проверку можно провести при помощи критерия Груббса. Для этого определяют:

а) для первого результата измерений   =   =1.686;

б) для последнего результата измерений   =   =2.13.

Так как и   =1.686 и   =2.13 значительно меньше табличного (критического) значения (при   =0.05 и n=20 è   =2.623),



Суммируя значения ранжированного вариационного ряда, определяем выборочное среднее

 =   =45.3 мм.

В графе 3 приведены разности между каждой составляющей выборки   и выборочным средним   , а в графе 4 их квадраты. Суммируя их найдем дисперсию выборки

 =   =1.269.

Для оценки рассеивания случайной величины относительно математического ожидания используются следующие характеристики: среднее квадратичное отклонение, коэффициент вариации, показатель точности и доверительный интервал.

Выборочное среднее квадратическое отклонение определяем по формуле

 =   =1.127.

Среднее квадратическое отклонение сводного результата определяем по формуле

 =   =0.252.

Выборочный коэффициент вариации определяем по формуле

 =   ∙100%=2.487%.

Коэффициент вариации показывает, как велико рассеивание результатов в сравнении со средним значением.

Показатель точности определяем по формуле

 =   ∙100%=0.556%.

Показатель точности свидетельствует о точности методики, по которой проводились испытания и получены результаты.

Доверительный интервал выборочных характеристик можно определить при помощи критерия Стьюдента по формуле

 -   ∙           +   ∙   ,

где   - критерий Стьюдента для уровня доверительной вероятности   , обычно принимаемой равной 0.95 или 0.99, и числа степеней свободы   =n-1 принимают по статистическим таблицам. Они имеются практически в каждом руководстве по математической статистике. В нашем случае:

а) при   =0.95 и   =20-1=19 получим 45.3-2.095∙0.252       45.3+2.095∙0.252 и после вычислений 44.77 мм       45.83 мм,

б) при   =0.99 и   =20-1=19 получим 45.3-2.859∙0.252       45.3+2.859∙0.252 и после вычислений 44.58 мм       46.02 мм.

То есть с увеличением уровня доверительной вероятности   доверительный интервал расширяется (45.83-44.77=1.06 мм и 46.02-44.58=1.44 мм).

Проверим теперь принадлежность первого и последнего результатов испытаний (ранжированного вариационного ряда) той же генеральной совокупности, как и остальные 18 результатов. Так как выборка имеет малый объем (n=20), то проверку можно провести при помощи критерия Груббса. Для этого определяют:

а) для первого результата измерений   =   =1.686;

б) для последнего результата измерений   =   =2.13.

Так как и   =1.686 и   =2.13 значительно меньше табличного (критического) значения (при   =0.05 и n=20 è   =2.623),

Список использованных источников

1.Дехтярь, Г.М. Метрология, стандартизация и сертификация: учебное пособие / Г. М. Дехтярь. – Москва: Курс, Инфра-М, 2018. – 149 с.

2.Дубовой, Н. Д. Основы метрологии, стандартизации и сертификации: учебное пособие / Н. Д. Дубовой, Е. М. Портнов. – Москва: Форум, Инфра-М, 2017. – 255 с.

3.Иванов, А.А. Метрология, стандартизация и сертификация: учебник / А. А. Иванов, А. И. Ковчик, А. С. Столяров. – Москва: Инфра-М, 2020. – 522 с.

4.Кириллов, В. И. Метрологическое обеспечение технических систем: учебное пособие / В. И. Кириллов. – Минск: Новое знание, 2017. – 424 с.

5.Мочалов, В. Д. Метрология, стандартизация и сертификация. Взаимозаменяемость и технические измерения: учебное пособие / В. Д. Мочалов, А. А. Погонин, А. Г. Схиртладзе. – 3–е изд., переработанное и дополненное. – Старый Оскол : Тонкие наукоемкие технологии, 2017. – 263 с.

6.Сергеев, А. Г. Метрология: учебник и практикум для СПО: для студентов образовательных учреждений среднего профессионального образования / А. Г. Сергеев, В. В. Терегеря. – 2-е изд., переработанное и дополненное. – Москва: Юрайт, 2017. – 421 с.

7.Хромой, Б.П. Метрология, стандартизация и сертификация: учебник для студентов и аспиранто, / Б. П. Хромой. – Москва: Горячая линия — Телеком, 2018. – 432 с.

8.Шишмарёв, В. Ю. Метрология, стандартизация и сертификация: учебник / В. Ю. Шишмарёв. – Ростов-на-Дону: Феникс, 2019. – 429 с.

9.Шишмарёв, В. Ю. Метрология, стандартизация, сертификация, техническое регулирование и документоведение: учебник: / В. Ю. Шишмарев. – Москва: Курс, Инфра-М, 2018. – 311с.