Геометрия 9. 1. Найдите тангенс угла, изображённого на рисунке. 2
 Скачать 144.5 Kb.
|
|
1.  Найдите тангенс угла, изображённого на рисунке. 2.  На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC. 3.  На рисунке изображена трапеция ABCD. Используя рисунок, найдите  .4.  На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.5.  На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.6.  Площадь одной клетки равна 1. Найдите площадь закрашенной фигуры.7.  На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.8.  На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали. 9.  На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.10. 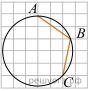 Найдите угол ABC. Ответ дайте в градусах. 1. Найдите тангенс угла, изображённого на рисунке. Решение.  Углы  и  в сумме образуют развёрнутый угол  Значит,  Рассмотрим прямоугольный треугольник, изображённый на рисунке. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:   Ответ: -1,5. 2. На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC. Решение. Из рисунка видно, что длина стороны AC равна 10. Длина средней линии равна половине длины стороны AC, следовательно, 5. Ответ: 5. 3. На рисунке изображена трапеция ABCD. Используя рисунок, найдите .Решение. Косинус угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе. Треугольник BAH — прямоугольный, поэтому  Вычислим по теореме Пифагора длину гипотенузы AB:  Тогда  Ответ: 0,8. Примечание. Обращаем внимание читателей, что для угла HBA прилежащим катетом является BH, а противолежащим AH. 4. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.Решение.  Расстояние от точки А до середины отрезка ВС равно трем сторонам клетки, или 3 см.Ответ: 3. 5. На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.Решение. Из рисунка видно, что длина большего катета равна 5. Ответ: 5 6. Площадь одной клетки равна 1. Найдите площадь закрашенной фигуры.Решение. Найдём площадь данной фигуры по формуле Пика: S = В + Г/2 − 1 где В — число узлов сетки внутри фигуры, Г — число узлов сетки на границе фигуры, включая вершины. Получаем: S = 5 + 8/2 − 1 = 8. Ответ: 8. 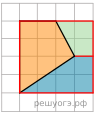 Приведём другое решение.Площадь данной фигуры равна разности площади квадрата и двух трапеций:  7. На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.Решение.  Площадь параллелограмма равна произведению стороны на высоту, проведенную к данной стороне: Ответ: 42 8. На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали. Решение.  По рисунку видно, что длина большей диагонали равна 12.Ответ: 12. 9. На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.Решение. Посчитаем количество клеток внутри закрашенной области: их 19. Ответ: 19. 10. Найдите угол ABC. Ответ дайте в градусах. Решение.  Центральный угол AOC равен 135°. Большая дуга AC равна 360°-135°=225°. Угол ABC опирается на эту дугу, но является вписанным и равен половине этой дуги, т. е. 112,5°.Ответ: 112,5. |