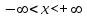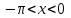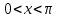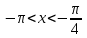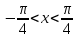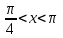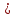1. Область определения функции функция определена при всех действительных значениях аргумента
 Скачать 171.31 Kb. Скачать 171.31 Kb.
|
|
1.б) 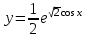 . .1. Область определения функции: функция определена при всех действительных значениях аргумента, 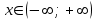 . .2. Пересечение графика функции с координатными осями и промежутки знакопостоянства: 1) с осью абсцисс: пересечения нет, поскольку показательная функция не пересекает ось абсцисс. 2) с осью ординат:  . Пересечение в точке . Пересечение в точке 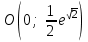 . .Промежутки знакопостоянства.
3. Четность/нечетность функции: 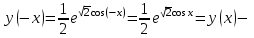 четная функция. четная функция. 4. Периодичность: функция периодическая с периодом 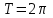 . .5. Асимптоты: а) вертикальные асимптоты – отсутствуют, т.к. функция непрерывна. б) наклонные асимптоты: 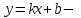 общее уравнение наклонных асимптот: общее уравнение наклонных асимптот: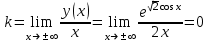 , , 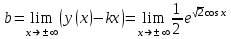 не существует. не существует.Наклонные асимптоты отсутствуют. 6. Монотонность и экстремумы: найдем производную функции:  . .Найдем точки, в которых производная функции обращается в ноль или не существует: 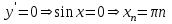 , , 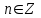 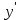 и определена на всей области определения функции. Исследуем поведение на одном периоде. и определена на всей области определения функции. Исследуем поведение на одном периоде.
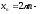 точки максимума, точки максимума, 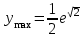 , ,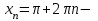 точки минимума, точки минимума, 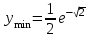 . .7. Интервалы выпуклости-вогнутости функции и точки перегиба: найдем вторую производную функции: 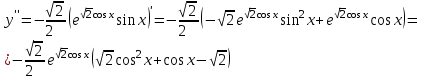 . .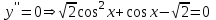 , пусть , пусть 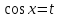 , тогда получаем квадратное уравнение: , тогда получаем квадратное уравнение: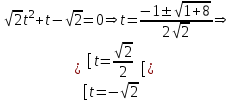 . . 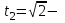 посторонний корень, тогда посторонний корень, тогда 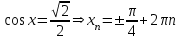 , ,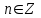 . .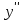 определена на всей области определения функции. Исследуем поведение на одном периоде. определена на всей области определения функции. Исследуем поведение на одном периоде.
 точки перегиба. точки перегиба.8. График функции. 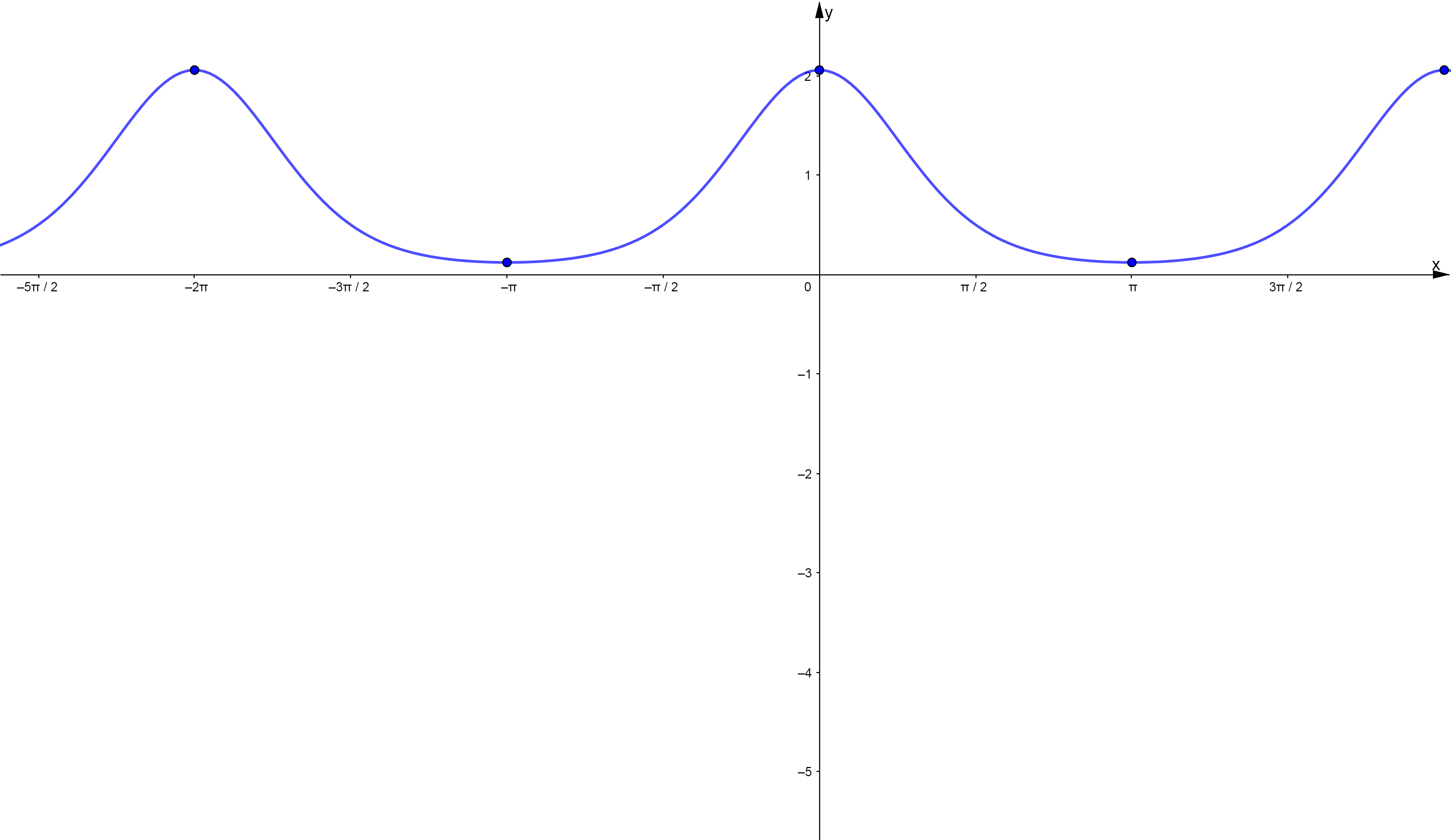 |