ОДУ 1. 1. Задача Коши условие задано в "начальной точке"
 Скачать 18.36 Kb. Скачать 18.36 Kb.
|
|
Часть 3. ОДУ. 1.1 Введение Будем рассматривать только уравнения разрешимые относительно старшей производной т.е. полагать 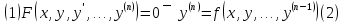 . И только те уравнения, имеющие единственное решение в каждой точке пространства. Т.е. самые простейшие уравнения. . И только те уравнения, имеющие единственное решение в каждой точке пространства. Т.е. самые простейшие уравнения. 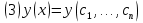 . В зависимости от того, как задаются условия для однозначности параметров, разделяются на задачи Коши и краевые задачи. . В зависимости от того, как задаются условия для однозначности параметров, разделяются на задачи Коши и краевые задачи.1. Задача Коши: условие задано в “начальной точке” 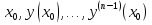 . .2. Краевая задача: условие на границах 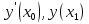 (в качестве примера). (в качестве примера). Будем заниматься задачей Коши в следующей постановке: 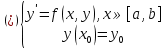 Как известно достаточно выполнение условий: 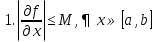 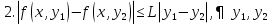 Будем полагать что они выполнены. Приближенным решением называется табличная функция такая что 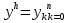 и и 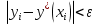 на некоторой сетке на некоторой сетке 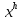 (будем полагать что она равномерная, но это не обязательно). Формулу для нахождения табличной функции будем называть вычислительной схемой: (будем полагать что она равномерная, но это не обязательно). Формулу для нахождения табличной функции будем называть вычислительной схемой: 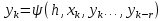 Классификация: a) 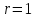 – одношаговая (если же схема многошаговая – одношаговая (если же схема многошаговая 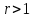 , то она требует расчета в стартовых точках , то она требует расчета в стартовых точкахб) Если функция не содержит 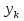 , то она называется явной. Если входит, то на каждом шаге понадобится решать уравнение относительно , то она называется явной. Если входит, то на каждом шаге понадобится решать уравнение относительно 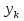 . Не всегда явные формулы лучше. . Не всегда явные формулы лучше.1.2 в) Если функция представима в виде: 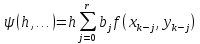 То метод называется конечно-разностным. Будем рассматривать только методы решения ОДУ первого порядка, т.к. высшего порядка может быть решено теми же способами. Связано это с тем, что уравнение первого порядка, разрешенное относительно старшей производной, может быть представлено в виде системы: То метод называется конечно-разностным. Будем рассматривать только методы решения ОДУ первого порядка, т.к. высшего порядка может быть решено теми же способами. Связано это с тем, что уравнение первого порядка, разрешенное относительно старшей производной, может быть представлено в виде системы: 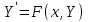 . Формулу вычислительной схемы можно использовать и для векторов. Самый простой способ эквивалентного преобразования: . Формулу вычислительной схемы можно использовать и для векторов. Самый простой способ эквивалентного преобразования: 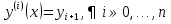 Это возможно только для задачи Коши т.к. начальные условия представимы в виде вектора. Понятие сходимости и устойчивости вычислительной схемы Выделяют два основных типа ошибок: 1. Ошибка дискретизации 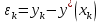 – связана с заменой непрерывного дискретным (переход к табличной функции) – связана с заменой непрерывного дискретным (переход к табличной функции)2. Ошибка вычислительная 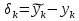 – связанная с неточным решением уравнения в вычислительной схеме – связанная с неточным решением уравнения в вычислительной схеме3. Полная ошибка 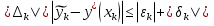 . . Поведение ошибок противоречиво, уменьшая одну – увеличиваем другую. Говорят, что вычислительная схема сходится если 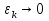 при при 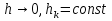 . Дробление сетки. . Дробление сетки.Схема называется устойчивой, если сколько бы мы вычислений не сделали, погрешность сильно не растет (ограничена постоянной независимой величиной). Хорошая схема должна быть сходящейся и устойчивой. Если мы подставим точное значение решения ОДУ в вычислительную схему, то точного равенства не будет и будет разница между левой и правой частью: 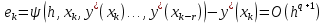 Которая называется ошибкой аппроксимации. Метод аппроксимирует с порядком 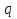 , если верно второе равенство. Для теории часто бывает удобной. , если верно второе равенство. Для теории часто бывает удобной.Метод Эйлера На некоторой равномерной сетке возьмем произвольную точку 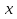 , такую что , такую что 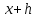 также входит в также входит в 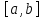 . Воспользуемся тем, что по формуле Тейлора . Воспользуемся тем, что по формуле Тейлора 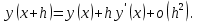 Приводим к Приводим к 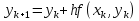 . Геометрический смысл в построении ломаных. Простейший метод – одношаговый, явный и конечно-разностный. Нас интересует сходимость и в дальнейшем покажем, что: . Геометрический смысл в построении ломаных. Простейший метод – одношаговый, явный и конечно-разностный. Нас интересует сходимость и в дальнейшем покажем, что: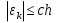 Для получения 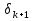 вычтем уравнения (с точным решением и с приближенным) друг из друга вычтем уравнения (с точным решением и с приближенным) друг из друга 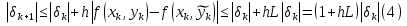 . Применим эту формулу . Применим эту формулу 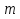 раз и тогда: раз и тогда: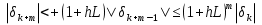 Т.к. 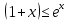 , то , то 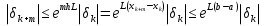 – метод устойчив. – метод устойчив. |
