авиационные тренажеры контрольная. Решение дифференциальных уравнений

• Название: Решение дифференциальных уравнений
• Дата: 19.12.2021
• Размер: 135.71 Kb.
• Имя файла: авиационные тренажеры контрольная.docx
• Тип: Решение; #309439

Решение дифференциальных уравнений
Математическое описание процессов, протекающих во времени, выполняется с помощью дифференциальных уравнений, т. е. уравнений, в которые входят как параметры состояния объекта или явления, так и их производные по времени. В математических и имитационных моделях, разрабатываемых для авиационных тренажеров, уравнения приводят к так называемой форме Коши, когда в уравнения входят параметры и их производные только первого порядка. Дополнительным требованием является приведение уравнения к такому виду, чтобы в левой части уравнения находились только производные, а в правой части производных не было:

, (1)

где x – переменная (параметр состояния); u – параметры управления; t– время.

Решение дифференциальных уравнений в реальном масштабе времени предполагает расчет правых частей уравнения вида (1) и выполнение операции интегрирования.

В аналоговых вычислительных устройствах алгебраические операции по вычислению правой части выполняются, как правило, с помощью потенциометрических счетно-решающих схем, суммирующих и инвертирующих операционных усилителей, а для выполнения интегрирования применяются следующие устройства:

- интегрирующие двигатели постоянного и переменного тока;

- электромеханические интеграторы или интегрирующие электроприводы;

- интегрирующие операционные усилители.

Электрические двигатели с возбуждением от постоянных магнитов или с независимым возбуждением являются наиболее простыми в реализации интеграторами. Если к якорю электродвигателя постоянного тока с возбуждением от постоянных магнитов приложено напряжение U_вх, то угловая скорость вращения вала двигателя будет пропорциональна величине напряжения:

. (2)

Угол поворота выходного вала представляет собой интеграл от угловой скорости и определяется из уравнения (2):

. (3)

Величина коэффициента k_φ у интегрирующего двигателя может изменяться под влиянием изменения нагрузки на выходном валу, трения в подшипниках, влияния реакции якоря, что приводит к появлению погрешностей интегрирования.

Для электродвигателя постоянного тока с независимым возбуждением справедливо следующее уравнение для входного напряжения:

, (4)

где Е – противоэлектродвижущая сила; I – ток якоря; R – сопротивление якоря электродвигателя.

Противоэлектродвижущая сила пропорциональна угловой скорости вращения якоря электродвигателя ω_я и магнитному потоку Ф

Е = Сω_яФ. (5)

Угловая скорость вращения якоря электродвигателя определяется соотношением

, (6)

так как падение напряжения в цепи якоря обычно невелико ввиду малости сопротивления R. Тогда угол поворота выходного вала определится интегралом

. (7)

Формулы (3) и (7), определяющие угол поворота выходного вала двигателя с возбуждением от постоянных магнитов и с независимым возбуждением, составлены без учета инерции вращающихся частей двигателя. Работа электродвигателя с учетом инерции его вращающихся частей описывается дифференциальным уравнением

, (8)

где Т_д– электромеханическая постоянная времени двигателя; k_φ – коэффициент пропорциональности.

Постоянная времени Т_д зависит от момента инерции якоря электродвигателя, сопротивления обмотки якоря и трения в подшипниках. Обычно Т_д = 0,01 … 0,03 с.

Произвести точное интегрирование с помощью электродвигателя невозможно. Это объясняется тем, что коэффициент k_φизменяется в зависимости от реакции якоря и нагрузки на вал двигателя. Для выполнения интегрирования с более высокой точностью применяются электромеханические интегрирующие приводы. Их точность практически не изменяется с увеличением нагрузки на валу.

В состав интегрирующего электропривода (рис.1) входят усилитель, интегрирующий электродвигатель, тахогенератор.



Рис.1. Схема интегрирующего электропривода

С выходным валом электродвигателя соединен подвижный элемент датчика сигналов (движок потенциометра или ротор сельсина). Входное напряжение пропорционально интегрируемой величине и подается обычно с потенциометрической счетно-решающей схемы. Оно сравнивается с напряжением тахогенератора и результат сравнения в виде разности напряжений подается на вход усилителя:

. (9)

Выходное напряжение усилителя определяется выражением

U_вых = k_yU_c, (10)

где k_y – коэффициент усиления усилителя.

Напряжение U_вых приложено к обмотке управления двигателя, который стремится вращать выходной вал со скоростью . Напряжение тахогенератора пропорционально угловой скорости вращения привода, т. е.

. (11)

При достаточно большом коэффициенте усиления усилителя устанавливается скорость вращения, при которой напряжение тахогенератора незначительно отличается от входного напряжения, т. е. U_тг ≈ U_вх и поэтому U_c<< U_вх. Таким образом, между входным напряжением и скоростью вращения выходного привода существует зависимость

. (12)

Следовательно, угол поворота выходного вала интегрирующего привода пропорционален интегралу от входного напряжения по времени:

. (13)

Угол φ является выходной величиной привода и с помощью датчика сигнала может быть преобразован в электрический сигнал.

Интегрирующий привод должен обладать высокой точностью, выполнять операцию интегрирования при изменении входного напряжения U_вх в широком диапазоне и обладать стабильностью характеристик при продолжительной работе.

Ошибка интегрирующего привода определяется погрешностью в скорости вращения выходного вала. Применение в приводе скоростной обратной связи способствует тому, что привод как в установившемся, так и в переходном режиме является практически идеальным интегрирующим звеном. Установившаяся ошибка в воспроизведении интеграла входного сигнала с помощью привода может с увеличением времени интегрирования возрастать.

Интегратор на операционном усилителе представлен на рис.2.





Рис.2. Интегратор на операционном усилителе


Для получения интегрирующих свойств в цепь обратной связи операционного усилителя включается емкость С. Выходной сигнал такой схемы описывается уравнением

. (14)

Точность выполнения интегрирования рассмотренной схемы зависит от погрешности операционного усилителя. Наибольшее влияние на точность операционного усилителя оказывает нестабильность нулевого уровня или дрейф выходного напряжения с течением времени. Дрейф U_вых проявляется в возникновении на выходе усилителя некоторого напряжения при нулевом входном напряжении. Дрейф выходного напряжения операционного усилителя объясняется нестабильностью напряжения источников электропитания, изменением характеристик отдельных элементов схемы усилителя. Для уменьшения дрейфа нулевого уровня применяют схемы операционных усилителей с параметрической компенсацией дрейфа и с автоматической стабилизацией нулевого уровня.

В системах цифрового моделирования для интегрирования дифференциальных уравнений требуется применение методов численного интегрирования.

Численное определение квадратур и численное интегрирова­ние обыкновенных дифференциальных уравнений относятся к классическим хорошо разработанным разделам вычислительной математики, а соответствующее программное обеспечение – к стандартному обеспечению ЦВМ. Однако проблемная ориента­ция на те динамические системы, которые составляют модельную основу авиационных тренажеров, позволяют указать наиболее рациональные алго­ритмы и методы численного интегрирования.

Напомним, что рассматривается векторное дифференциальное уравнение вида (1). Векторная функция векторного аргумента f может быть не­гладкой и даже разрывной (с разрывами первого рода). Это обусловлено либо способом аппроксимации реальных гладких характеристик, либо отражает сам вид этих характеристик. Последнее имеет место, в частности, при имитации САУ с существенными нелинейностями, при ими­тации влияния сухого трения и др. Эти особенно­сти функции f вносят некоторую специфику в применение мето­дов численного интегрирования. Другую специфику составляет режим реального времени, накладывающий ограничение на объем вычислений рассматриваемого алгоритма численного интегрирования.

При дискретном цифровом моделировании текущее время разбивается на интервалы (шаги) длительностью hи фиксируются моменты начала каждого шага t_k =kh(k = 0, 1, 2,...). В общем виде задача численного интегрирования может быть сформулирована следующим образом. Считая известными значения вектора состояния x[t_k] в k-й момент времени, вектора управления u[t_k], аналитические формулы для расчета , требуется определить x[t_k+1]. Очевидно, что решение задачи имеет вид

. (15)

Вся сложность заключается в том, что в практически значимых задачах интеграл в формуле (15) аналитически вычислить не удается. Поэтому для его вычисления используют приближенные численные методы.

Поскольку в момент времени t_kпредсказать поведение управляющего сигнала u(t)при t>t_k, как правило, невозможно, то первое упрощение заключается в принятии гипо­тезы: u(t) = u(t_k)на интервале . Погрешность, порожденная этой гипотезой, в одинаковой мере присуща всем методам численного интегрирования и зависит лишь от дискретности опроса входной величины и длительности шага интегрирования h, поэтому в дальнейшем рассматривать ее не будем.

Алгоритмы численного интегрирования будем рассматривать для процедуры вида

, (16)

подразумевая, что управление на интервале постоянно. Задача численного интегрирования заключается в приближенном вычислении интеграла .

Простейшим методом интегрирования является метод Эйлера, в котором интеграл вычисляется по информации о производной в левом конце отрезка времени :

, (17)

где h – величина шага численного интегрирования, равная разности (t_k+1-t_k); – значение переменной x в момент времени t_k, определенное численно.

Погрешность на одном шаге интегрирования для случая непрерывной функ­ции имеет порядок О(h²).

На рис.3 приведена графическая интерпретация метода Эйлера, где x(t)является точным решением уравнения при x[t_k] = ; – численноерешение, получаемое методом Эйлера при тех же начальных условиях .

В методе Эйлера численное решение ищется путем линейного про­­­­гноза вперед по касательной, угол наклона которой α вычисляется как f( , t_k). Очевидно, что при сохранении знака второй производной функции f ошибка решения метода Эйлера монотонно возрастает. Необходимо применение специальных мер для повышения точности метода численного интегрирования.

В зависимости от способа решения проблемы повышения точности методы численного интегрирова­ния разделяются на две большие группы: одношаговые методы и многошаговые методы.

Кпервой группе относятся методы Рунге – Кутта. Идея этих методов состоит в повышении точности за счет получении дополнительной информации о поведении функции f(x(t), t)в некоторых промежуточных точках отрезка . Получить эту информацию можно только при условии, что нам будет известно значение , причем это значение может быть приближенным, определенным численно. Именно на этой идее и основаны методы Рунге – Кутта. По правилу, аналогичному рассмотренному выше методу Эйлера, вычисляется первое приближенное значение и это значение используется для расчета прогнозного значения функции . Следующее приближенное значение вычисляется не по значению f( , t_k), а по некоторой линейной комбинации значений f( , t_k) и , рассчитанному на предыдущем прогнозе.

Число точек, в которых дополнительно определяются зна­чения и ,является параметром метода. Один из вариантов метода Рунге – Кутта второго порядка приведен на рис.4.

На первом этапе осуществляется вычисление прогнозного значения по методу Эйлерана момент времени . С использованием этого значения на втором шаге вычисляется и осуществляется расчет значения :

. (18)

Геометрической интерпретацией расчета второго шага является «движение» из точки ( , t_k) на плоскости OXt вдоль прямой с углом наклона α₁=arctg( ) до пересечения с прямой t=t_k+1.

«Платой» за повышение точности является необходимость несколько раз (в рассмотренном нами примере – 2 раза) на каждом шаге численного интегрирования рассчитывать значение функции , что требует значительных вычислительных затрат.

Рис.3. Графическая интерпретация численного интегрирования по методу Эйлера

Рис.4. Графическая интерпретация численного интегрирования по методу Рунге – Кутта 2-го порядка

Широко известен метод Рунге — Кутта четвертого порядка со следующими параметрами метода:

(19)

Этот метод требует вычисления 4-х значений функции f на один шаг численного интегрирования и обеспечивает 5-й порядок точности по величине h. Он применяется в ряде авиационных тренажерах зарубежной разработки. Однако в отечественных цифровых авиационных тренажерах разработки 80-90 гг. прошлого столетия ограниченная вычислительная производительность ЭВМ типа М-6000 и СМ-2М не позволила применить методы Рунге – Кутта, и для повышения точности интегрирования используются многошаговые методы численного интегрирования.

Основная идея повышения точности интегрирования в многошаговых методах базируется на привлечении в качестве дополнительной информации о прогнозе поведения функции f(x(t), t) на интервале [t_k,t_k+1] рассчитанных ранее значений этой функции в m последних точках интегрирования: f( ,t_k-1), f( ,t_k-2), … f( ,t_k-m). По значениям функции в точках f( ,t_k), f( ,t_k-1), f( ,t_k-2), … f( ,t_k-m) на ин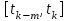тервале строится интерполяционный полином порядка m, и поведение функции f(x(t), t) на интервале считается совпадающим с этим полиномом. Поскольку коэффициенты этого интерполяционного полинома являются детерминированными функциями величин f( ,t_k), f( ,t_k-1), f( ,t_k-2), … f( ,t_k-m), вычисление интеграла в формуле (16) можно произвести аналитически, в результате чего получаются итоговые формулы численного интегрирования вида

(20)

Геометрической интерпретацией многошагового метода является «движение» из точки ( ,t_k) на плоскости OXt вдоль кривой, производная которой описывается прогнозом значений построенного интерполяционного многочлена для функции f до пересечения с прямой t= t_k+1.

Многошаговые методы требуют лишь однократного вычисле­ния правых частей на каждом шаге (остальные точки хранятся в скользящей очереди данных в памяти ЦВМ), общее число операций на каждом шаге немногим больше, чем требует метод Эйлера. В то же время точность многошаговых методов на шаге значительно выше, чем у метода Эйлера.

Описанный здесь подход и формула (20) не исчерпывают всего многообразия многошаговых методов численного интегри­рования. В расчетные формулы могут также входить значения вектора состояния в некоторых предыдущих точках, существует большой класс формул интегрирования неявного типа, требующих для разрешения итерационных процедур. Рассмотрим некоторые расчетные формулы, применяющиеся в отечественных АТр.

Метод Адамса второго порядка имеет вид

, (21)

обладает третьим порядком точности по h и применяется в тех случаях, когда шаг дискретизации мал (не более 20 мс).

Метод Адамса третьего порядка имеет вид

(22)

обладает четвертым порядком точности по h и применяется в программно-математическом обеспечении авиационных тренажеров в несколько модифицированном виде, именуемом методом Симпсона:

(23)

Недостатком многошаговых методов при использовании их в авиационных тренажерах является искажение управ­ляющих сигналов u(t), входящих в уравнение , так как вместе с текущим значением управления метод будет учитывать значения уп­равляющего сигнала в предыдущих m точках. Это особенно проявляется в динамике полета при решении та­ких задач, как уточнение прицеливания, дозаправка в воздухе, режим посадки и другие. Одношаговые методы лишены этого недостатка и адекватно учитывают внешние управляющие сигналы.

Другим важным вопросом является вычисление первых mзначений х(t)иf(x(t), t), необходимых для запуска многошагового мето­да. В цифровых имитаторах АТр при начальном запуске все m значений назначают равными начальным условиям.

Помимо точности на шаге при выборе метода численного интегрирования следует учитывать свойство вычислительной устойчивости, т. е. сходимости численного решения к точному в условиях накопления вычислительной и методической погрешности. В частности, от методов численного интегрирования в большей степени требуется адекватное воспроизведение частотных характеристик моделируемых процессов в диапазоне частот, значимых для привития обучаемым профессионально важных навыков и умений. С этой точки зрения одношаговые методы Рунге – Кутта также обладают преимуществом над многошаговыми методами.

Рассмотренные выше методы численного интегрирования являются универсальными и применимы к любым обыкновенным дифференциальным уравнениям первого порядка. Протекание таких процессов как динамика и кинематика полета, навигационное перемещение ЛА относительно Земли и ряд других, описываются с помощью специфических дифференциальных уравнений, допускающих при определенных допущениях аналитические решения. Наличие этих аналитических решений позволяет разработать для интегрирования этих групп дифференциальных уравнений специализированные методы численного интегрирования, которые обеспечивают требуемую точность при вычислительных затратах, сопоставимых с методом Эйлера, но без недостатков, присущих многошаговым методам интегрирования. Эти методы будут рассматриваться нами при изучении конкретных имитаторов и систем тренажеров.