10. Алгебраические кривые порядка над полем. Кривые второго порядка. Неособые точки кривой и неособые кривые
 Скачать 3.19 Mb.
|
|
10. Алгебраические кривые порядка над полем. Кривые второго порядка. Неособые точки кривой и неособые кривые.    11. Эллиптические кривые над полем. Форма Вейерштрасса. Бесконечно удаленная точка. Дискриминант и инвариант эллиптической кривой. Суперсингулярные кривые.         12. Группа точек эллиптической кривой.     13. Эллиптические кривые над конечными полями. Точки конечного порядка. Порядок эллиптической кривой. Неравенство Хассе и его применение.  Порядком  точки  на эллиптической кривой называется такое наименьшее натуральное число, что  ; разумеется, такого конечного может и не существовать, в этом случае мы будем говорить о точке бесконечного порядка. Часто требуется найти точки конечного порядка на эллиптической кривой, в особенности на эллиптических кривых, определенных над полем рациональных чисел  .Пример 4.4 Найти порядок точки  на  .Решение. Применяя (4.1), находим, что  ,  . Поэтому  и, следовательно,  . Тем самым порядок может быть равен 2, 3 или 6. Но  , а если бы имела порядок 3, то было бы  , что неверно. Итак, имеет порядок 6.Каждая точка P эллиптической кривой над простым полем Ɛ(Fp ) образует циклическую подгруппу G группы точек эллиптической кривой • Порядок циклической подгруппы группы точек эллиптической кривой (число точек в подгруппе) называется порядком точки эллиптической кривой • Точка P на Ɛ(Fp ) называется точкой порядка q, если: q P=O где q – наименьшее натуральное число, при котором выполняется данное условие    14. Эллиптические кривые над GF(2n ).  Эллиптические кривые в GF(2 в степени n) Вычисление в группе эллиптической кривой может быть определено в поле GF(2n). В соответствии с лекциями 5-6, где мы говорили, что элементы множества в этом поле — n -битовые слова, которые можно интерпретировать как полиномы с коэффициентом в GF(2), сложение и умножение этих элементов такое же, как сложение и умножение полиномов. Для того чтобы определить эллиптическую кривую в GF(2n), необходимо только изменить кубическое уравнение. Общее уравнение y2 + xy = x3 + ax2 + b где  . Обратите внимание, что значение x, y, a и b — полиномы, представляющие n -битовые слова.Нахождение инверсии Если P = (x, y), то (–P) = (x, x + y). Нахождение точек на кривой Мы можем написать алгоритм для нахождения точек на кривой, используя генераторы для полиномов, которые рассматривали в лекциях 9-10. Но разработку этого алгоритма оставляем как упражнение. Далее следует очень тривиальный пример. Пример 15.8 Мы выбираем GF (23) с элементами (0,1, g, g2, g3, g 4, g5, g6), использующими неприводимый полином f (x) = x3 + x +1. Этому соответствует полином g3 + g +1 = 0 или g3 = g + 1. Другие степени g могут быть вычислены, как это показано ниже.
Используя эллиптическую кривую y2 + xy = x3 + g3x2 + 1, a = g3 и b = 1, мы можем найти точки на этой кривой, как это показано на рисунке 15.6.  Рис. 15.6. Точки на эллиптической кривой в GF (2 в степени n) Сложение двух точек Правила для сложения точек в GF(2n) немного отличаются от правил GF(p). 1. Если P = (x1, y1), Q = (x2, y2),  ,  , то R = (x3, y3) = P + Q может быть найден как 2.Если Q = P, то R = P + P (или R = 2P ) и может быть найден как  Пример 15.9 Пусть нам надо найти R = P + Q, где P = (0,1) и Q = (g2,1). Мы имеем  и R = (g5, g4).Пример 15.10 Пусть нам надо найти R = 2P, где P = (g2,1). Мы имеем  и R = (g6, g5).Умножение точек на константу Для того чтобы умножить точку на константу, точки должны складываться непрерывно согласно правилу R = 2P. 15. Алгоритмы сложения и удвоения точек эллиптических кривых.       16. Алгоритмы генерации эллиптических кривых и криптографически надежных параметров кривых.    17. Построение псевдослучайных последовательностей на эллиптических кривых. Введение. Постановка задачи. Псевдослучайные последовательности используются для генерации секретных ключей шифрования, для вычисления цифровой подписи и для работы многих алгоритмов аутентификации. Для построения псевдослучайных последовательностей используются линейные рекуррентные последовательности на эллиптической кривой. Поставим задачу проанализировать существующие генераторы на эллиптической кривой и разработать генератор псевдослучайных последовательностей на эллиптической кривой с использованием квадратичных полей Галуа. Анализ генераторов построенных на точках эллиптической кривой Генератор псевдослучайных последовательностей должен удовлетворять следующим двум требованиям, предложенным в работе: Статистической безопасностью: последовательность, созданная генератором псевдослучайных чисел должна статистически ничем не отличаться от абсолютно случайной последовательности. Криптографической безопасности: возможности зная  -битов последовательности, предсказать следующий или -бит.Эллиптическая кривая широко используется для построения криптосистем []. Одним из инструментов построения генераторов псевдослучайных последовательностей является эллиптическая кривая над конечным полем.  Следует отметить также статистическую безопасность генератора псевдослучайных чисел, построенного на базе арифметической прогрессии на эллиптической кривой. Она обладает хорошими статистическими свойствами, что показано в работе []: равномерностью распределения элементов арифметической прогрессии для большого , также указан порядок величины отклонения от равномерности  Для случая, при котором известна разность G и старшие биты  в работе Гутиэрехом и Ибиасом предложен эффективный алгоритм нахождения  для генераторов, построенных на базе арифметической прогрессий на эллиптической кривой, следовательно, он не обладает криптографической безопасностью. Значит, секретным ключом в генераторе псевдослучайных чисел (1) должны являться  . В этом случае не известны эффективные алгоритмы предсказания бит, и генератор (1) является криптографически безопасным. В работе в более общем виде рассмотрены генераторы псевдослучайных последовательностей типа арифметическая прогрессия на эллиптической кривой. Пусть порядок  . Последовательность  , удовлетворяющих рекуррентному соотношению:  , (2),называют EC-последовательностью порядка  – характеристическим многочленом над  . Используя обозначения EC-последовательностей, последовательность, заданная формулой (1), называется -последовательностью первого порядка и характеристическим многочленом . О последовательности, заданной формулой (2), известно, что период –последовательности (2) есть делитель периода ее характеристического многочлена . В работе [] показано, что наибольший период имеет примитивный многочлен над полем. Найдем примитивные многочлены второй степени, для чего воспользуемся следующей теоремой.  18. Схема симметричного шифрования на эллиптических кривых. Зашифрование информации (абонент А защищает сообщение М, предназначенное для абонента В) (рис. 12.1): А преобразовывает открытый текст М в точки эллиптической кривой; А выбирает секретный ключ К; А вычисляет закрытый текст С  Расшифрование информации (абонент В преобразует закрытый текст С) (рис. 12.2): В вычисляет обратный ключ (-К). В восстанавливает открытый текст М   Рис. 12.1. Прямое преобразование 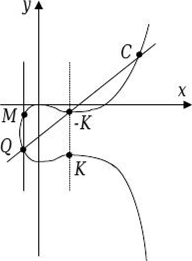 Рис. 12.2. Обратное преобразование Пример. Пусть задана кривая Е (СР(23)) вида у2 — X3 + X + 1. Зашифрование информации (абонент А защищает сообщение М, предназначенное для абонента В): А преобразовывает открытый текст М в точку эллиптической кривой  А выбирает секретный ключ К = (13, 7); А вычисляет закрытый текст  СРасшифрование информации (абонент В восстанавливает закрытый текст С, полученный от абонента А): В вычисляет обратный ключ (-К)  В восстанавливает открытый текст М  19. Схема асимметричного шифрования на эллиптических кривых. Реализовать схему асимметричного шифрования на эллиптических кривых.В алгоритмах асимметричного шифрования на эллиптических кривых должны быть определены следующие открытые параметры, общие для всех пользователей: конечное поле GF(p); эллиптическая кривая E(GF(p)); порядок n, который является простым числом; базовая точка Gпорядка n. Процедура генерации ключей осуществляется следующим образом. Каждый пользователь системы генерирует пару ключей следующим образом: выбирается случайное целое число d, 1 d n1; вычисляется точка Q dG. Секретным ключом пользователя является число d, открытым ключом – точка Q. Действия отправителя сообщения (абонент Aшифрует сообщение М, предназначенное для абонента B): Авыбирает случайное целое число k, 1 k n1; Авычисляет точку (x1, y1) kG; Авычисляет точку В; (x2, y2) kQ, используя открытый ключ Qпользователя Авычисляет c1 M x2 . Шифртекстом является набор C (x1, y1,c1) . Действия получателя сообщения (абонент Bрасшифровывает шифртекст С): Ввычисляет точку (x2 , y2 ) d(x1, y1) , используя свой секретный ключ d; Ввосстанавливает исходное сообщение M c1 x2 . 20. Схема цифровой подписи на эллиптических кривых.   21. Схема распределения ключей на эллиптических кривых.   22. Схема гибридного шифрования на эллиптических кривых.    23. Стандарт ЭЦП ГОСТ Р 34.10-2012 https://protect.gost.ru/v.aspx?control=8&baseC=-1&page=0&month=-1&year=-1&search=&RegNum=1&DocOnPageCount=15&id=172255&pageK=8074B207-9954-40FD-912E-20E8D0BFAA2E http://elib.osu.ru/bitstream/123456789/11745/1/92829_20190327.pdf |