трип. Контрольная работа тригонометрия. Решение Составим общее уравнение прямой ah используя вектор bc bc (C x b x c y b y ) (6278) (41)
 Скачать 95.88 Kb. Скачать 95.88 Kb.
|
Контрольная работа по математики №28 вариантБаталин Михаил МихайловичГ. Тюмень, ул. Мельникайте 127а, 289Задание 1Даны координаты вершин треугольника A(1, 3), B(2, 8), C(6, 7). Запишите общее уравнение его высоты AH. Решение: Составим общее уравнение прямой AH используя вектор BC: BC = (Cx-Bx ; Cy-By) = (6-2;7-8) = (4;-1) Уравнение прямой будет выглядеть следующим образов: 4x-1y+d=0, чтобы найти постоянную d подставим в уравнение координаты точки A. 4*1-1*3+d=0 4-3+d=0 1+d=0 d = -1 Ответ: Уравнение прямой AH: 4x-1y-1=0 или y = 4x-1 Задание 2В треугольнике ABC из вершины A проведены высота и медиана. Даны координаты вершины B (6, 5), уравнение высоты x + y = 2 и уравнение медианы 2x − 3y + 1 = 0. Найдите координаты x0, y0 вершины C Решение: Координаты вершины A можно найти как точку высоты AH и медианы AM: 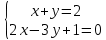 Умножим первое уравнение на 3 и найдем x 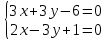 5x - 5 = 0 5x = 5 x = 1 Подставим x в первое уравнение и найдем y 1 + y -2 = 0 y – 1 = 0 y = 1 Координаты вершины A (1,1) Точка M имеет координаты 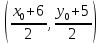 Точка C лежит на прямой BC, а точка M на медиане. Прямая ВС перпендикулярна высоте. Записываем уравнение BC: Ax + By – (Ax0 + By0) = 0 -x + y – (-6+5) = 0 -x + y + 1 = 0 Находим x0 и y0 с помощью системы уравнений: 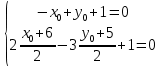 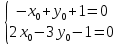 Умножим первое уравнение на 3 и найдем x 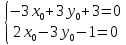 -x0 + 2 = 0 -x0 = -2 x0 = 2 Подставим x в первое уравнение и найдем y -2 + y0 + 1 = 0 y0 = 1 Ответ_:_Вершина_C_(2,_1)_Задание_3'>Ответ: Вершина C (2, 1) Задание 3Запишите общее уравнение плоскости, проходящей через точки M1(1,−2, 4) и M2(2,−1, 2) перпендикулярно плоскости x + 4y − 5z + 3 = 0. Решение: Плоскость p параллельна вектору плоскости p1 Уравнение плоскости через точку M0(x0, y0, z0) имеет следующий вид: A(x-x0) + B(y-y0) + C(z-z0) = 0 Плоскость p: Ax + By + Cz + D = 0 проходит через точки M1(1, -2, 4) и M2(2, -1, 2) и геометрический вектор n = (1, 4, -5) Найдем координаты отрезка M1M2 M1M2 = (x2 – x1, y2 – y1, z2 – z1) = (2 – 1, (-1) – (-2), 2 – 4) = (1, 1, -2) Подставим в уравнение плоскости координаты отрезка M1M2 х + 4у - 5z + d = 0 1 + 4*1 – 5*(-2) + d = 0 d = -15 Подставим полученные данные в уравнение плоскости Ответ_:_Координаты_проекции_точки_M_на_плоскость_это_точка_Q_(1,_-2,_1)_Задание_5'>Ответ: Общее уравнение плоскости x + 4y – 5z – 15 = 0 Задание 4Найдите координаты проекции точки M (3,−1,−3) на плоскость 2x + y − 4z + 4 = 0. Решение: Проекцией точки М на плоскости p называется Q пересечения плоскости p с прямой H, проходящей через точку М перпендикулярную к плоскости p. Допустим 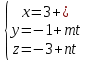 это прямая H проходящая через точку М и перпендикулярна плоскости p. Тогда за направляющий вектор прямой H можно взять вектор плоскости p. Вектор n = (2, 1, -4). Найдем координаты точки Q, присвоив l, m, n координаты вектора n. 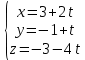 Подставим уравнение прямой H в уравнение плоскости: 2(3 + 2t) + (-1 + t) – 4(-3 – 4t) + 4 = 0 6 + 4t – 1 + t +12 + 16t + 4 = 0 4t + t + 16t + 6 – 1 + 12 + 4 = 0 21t + 21 = 0 21t = -21 T = -1 Подставим найденное значение в уравнение прямой H: 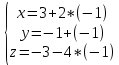 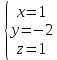 Ответ: Координаты проекции точки M на плоскость это точка Q (1, -2, 1) Задание 5Найдите коэффициент A в уравнении плоскости Ax + y + Cz + D = 0, проходящей через точки P (1, 1, 8), O (0, 0, 0) параллельно прямой 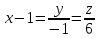 Решение: По условию задачи прямая параллельна плоскости, значит Al + Bm + Cn = 0 Из уравнения прямой получаем l = 1, m = -1, n = 6 и следующее уравнение: A – B + 6C = 0 На основании принадлежности точек P и O к плоскости получаем уравнение: A + B + 8C = 0 Решим систему уравнений: 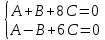 Вычтем второе уравнение из первого: 2B + 2C = 0 B = -C Допустим B = -1, а C = 1, подставим текущие значения в первое уравнение: A – 1 + 8 = 0 A = -7 Ответ_:Первая_прямая_пересекается_с_другими_прямыми_при_a_=_2и_c_=_1_Задание_7'>Ответ: Коэффициент A = -7 Задание 6 При каких значениях параметров a и c прямая  c пересекает две другие прямые: c пересекает две другие прямые:  и и  Решение: Найдем определители из уравнений 2-ой и 3-ей прямой:  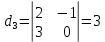 Т.к. определители не равны нулю то z из систем можно записать в следующем виде: 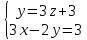 и и 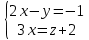 Найдем общее решение 2-ой прямой: 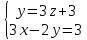 Умножим первое уравнение на 2 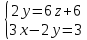 3x = 6z + 6 + 3 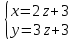 Докажем, что 1-ая и 2-ая прямые пересекаются: 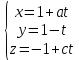 Прямые будут пересекаться при выполнение следующего равенства: (r2 – r1, l1, l2) = 0 r1 = (1, 1, -1), r2 = (3, 3, 0), l1 = (a, -1, c), l2 = (2, 3, 1) Подставляем значения: 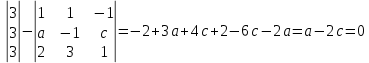 Найдем общее решение 3-ей прямой:  Умножим первое уравнение на 3, а второе на 2  3y = -3 – 2z – 4 3y = 2z + 7  Аналогично докажем, что 1-ая и 3-ья прямые пересекаются: (r3 – r1, l1, l3) = 0 r1 = (1, 1, -1), r3 = (  , ,  , 0), l1 = (a, -1, c), l2 = ( , 0), l1 = (a, -1, c), l2 = ( , ,  , 1) , 1)Подставляем значения:  Решим систему уравнений:  a = 2c, подставим это значение в первое уравнение: -4с + 2с + 2 = 0 -2с = -2 с = 1 подставим значение во второе уравнение: a = 2 * 1 a = 2 Ответ: Первая прямая пересекается с другими прямыми при a = 2иc = 1 Задание 7Найдите радиус сферы, если известно, что она касается двух плоскостей x − 2y + 2z + 22 = 0 и x − 2y + 2z + 10 = 0. Решение: Сфера — это множество точек пространства, равноудаленных от центра. Расстояние между точками сферы и центром является радиус сфера. d(p1,p2) равно двум радиусам сферы. Вычислим радиус сферы по формуле:   Т.к. это два радиуса: 4/2 = 2 Ответ: Радиус сферы R = 2 Задание 8Дана кривая 9x2 + 4y2 − 36x − 64y + 256 = 0. Докажите, что эта кривая — эллипс. Найдите координаты центра его симметрии. Найдите его большую и малую полуоси. Запишите уравнение фокальной оси. Постройте данную кривую. Решение: 1. Преобразуем уравнение: (9x2 – 36x) + (4y2 – 64y + 256) = 0 9(x – 2)2 + 4(y – 8)2 – 36 = 0 9(x – 2)2 + 4(y – 8)2 = 36 Введем новые переменные x1 = x – 2, y1 = y – 8 Тогда  Это уравнение определяет эллипс. 2. Центр симметрии точки О из уравнения эллипса: x – 2 = 0 x = 2 y – 8 = 0 y = 8 Центр эллипса находится в точке O (2, 8) 3. Большая (a) и малая (b) полуось: 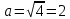 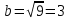 4. Для уравнения фокальной оси найдем координаты фокусов F1 и F2 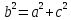 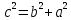 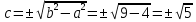 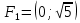 , , 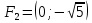 Уравнение фокальной оси: 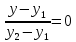 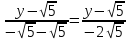 Умножим на 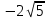 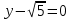 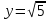 5. График кривой. 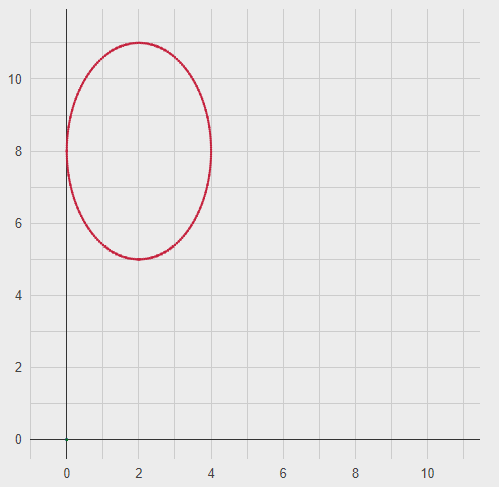 Задание 9Дана кривая x2 − 4x + 8y = 36. Докажите, что данная кривая — парабола. Найдите координаты её вершины. Найдите значение её параметра p. Запишите уравнение её оси симметрии. Постройте данную параболу. Решение: 1. Матрица квадратичной формы B: 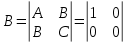 Определяем тип кривой, для этого составим характеристическое уравнение квадратичной формы: 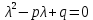 Находим p и q из уравнения: 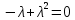 p = -1 q = 0 Находим корни уравнения матрицы B: 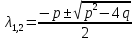 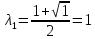 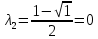 Так как одно из собственных чисел равно нулю, то кривая – парабола. 2. Преобразуем уравнение: (x2 – 4x – 4) + 8y – 36 + 4 = 0 (x – 2)2 + 8y – 32 = 0 x1 = x – 2 y1 = 8y – 32 Уравнение параболы: (x – 2)2 = -8(y – 4) Вершины параболы: x – 2 = 0 x = 2 y – 4 = 0 y = 4 3. Сравниваем последнее уравнение с каноническим уравнением параболы: (x – 2)2 = -2 * 4(y – 4) P = 4 4. Вершина параболы в точке (2, 4) Прямая параллельна ОУ и проходит через точку (2, 4), получили уравнение оси симметрии x = 2 5. 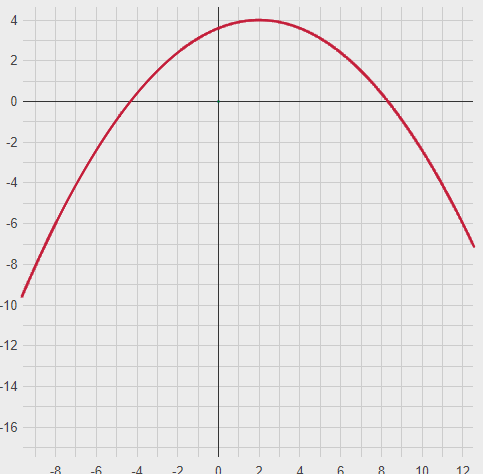 Задание 10Дана кривая x2 − 8xy + 7y2 + 6x − 6y + 9 = 0. Докажите, что эта кривая — гипербола. Найдите координаты её центра симметрии. Найдите действительную и мнимую полуоси. Запишите уравнение фокальной оси. Постройте данную гиперболу. Решение: 1. Матрица квадратичной формы B: 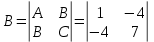 Определяем тип кривой, для этого составим характеристическое уравнение квадратичной формы: 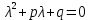 Вычислим p и q: 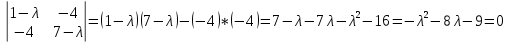 p = -8 q = -9 Находим корни уравнения матрицы B: 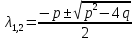 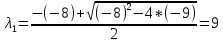 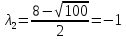 Так как собственные числа имеют разные знаки, то кривая – гипербола. Для собственного числа 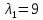 получаем систему: получаем систему: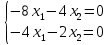 Если x1 = 1, x2 = -2, то единичный собственный вектор i1 имеет координаты i1 = (1, -2). Другой собственный вектор, отвечающий собственному числу 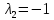 , может быть задан в виде j1 = (2, 1) таким образом, чтобы базис (i1, j1) был правым. , может быть задан в виде j1 = (2, 1) таким образом, чтобы базис (i1, j1) был правым.От старого базиса (O, i, j) перейдем к новому базису (O, i1, j1). При этом 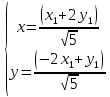 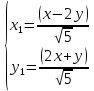 В новой системе координат уравнение данной кривой примет следующий вид: 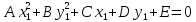 Подставим данные в уравнение:    Произведем преобразование параллельного переноса системы координат в новое начало О1 по формулам:    2. В системе координат (О1, i1, j1) гипербола имеет уравнение:  O1x2 = x – 2y + 1 = 0 O1y2 = 2x + y – 3 = 0 Решим систему уравнений:  Умножим второе уравнение на 2  5x = 5 x = 1 Находим y умножив первое уравнение на -4, а второе на 2  10y = 10 y = 1 Координаты точки центра симметрии O1 = (1, 1) 3. Действительная полуось a = 1, мнимая полуось b = 3 4. Фокальной осью является прямая y2=0 2x + y – 3 = 0 5.  |
