лабораторная работа базы данных. Лаб.3 Нормальные формы. 5. Нормализация реляционной модели Функциональные зависимости
 Скачать 146.22 Kb.
|
|
5. Нормализация реляционной модели 5.1. Функциональные зависимости  Функциональные зависимости– это особый вид ограничений целостности, а потому они предоставляют проектировщику способ отразить семантические зависимости между данными. Распознавание функциональных зависимостей представляет собой часть процесса выяснения смысла тех или иных данных. Например, тот факт, что поставщик проживает точно в одном городе можно отразить с помощью функциональной зависимости Номер поставщика Адрес поставщика.По сути, функциональная зависимость является связью типа «многие-к-одному» между множествами атрибутов внутри отношения. Дадим определение функциональной зависимости. Пусть R является отношением, а X и Y – произвольные подмножества множества атрибутов отношения R. Тогда Y функционально зависимо от X (или X функционально определяет Y)  тогда и только тогда, когда каждое значение множества X отношения R связано в точности с одним значением множества Y отношения R. Иначе говоря, если два кортежа отношения R совпадают по значению X, они совпадают и по значению Y.Например, отношение «Поставщик» удовлетворяет требованиям нескольких функциональных зависимостей: {№ поставщика}  {Имя поставщика}{№ поставщика} {Статус поставщика}{№ поставщика} {Адрес поставщика}{№ поставщика} {Имя поставщика, Статус поставщика, Адрес поставщика}{Имя поставщика} {Адрес поставщика}{Имя поставщика} {Статус поставщика}{Имя поставщика} {Адрес поставщика, Статус поставщика }Левая и правая части символической записи функциональной зависимости называются детерминантом и зависимой частью соответственно. Как следует из определения, детерминант и зависимая часть являются множествами атрибутов. Если множество содержит один атрибут, оно называется одноэлементным множеством и тогда фигурные скобки могут быть опущены: № поставщика Имя поставщикаУтверждение, что данная функциональная зависимость выполняется всегда, для всех возможных значений отношения, является ограничением целостности для отношения, а это значит, что при этом накладываются определенные ограничения на все его допустимые значения. Даже если ограничиться рассмотрением функциональных зависимостей, имеющих место в любой момент, полный набор функциональных зависимостей, выполняющихся для всех допустимых значений заданной переменной-отношения, может быть очень большим. Необходимо минимизировать множество функциональных зависимостей до некоторых пределов. Задача поиска такого подходящего множества представляет практический интерес. Очевидным способом сокращения существующего набора функциональных зависимостей является исключение из него тривиальных зависимостей, т.е. зависимостей, которые не могут не выполняться. Функциональная зависимость является тривиальной тогда и только тогда, когда правая часть ее символической записи является подмножеством левой части. Одни функциональные зависимости подразумевают другие зависимости. Для данного множества зависимостей S замыканием S+ называется множество всех функциональных зависимостей, подразумеваемых зависимостями множества S. Полную и исчерпывающую основу для вычисления замыкания S+ для заданного множества S обеспечивают правила логического вывода (аксиомы) Армстронга. Пусть заданы A,B,C – произвольные подмножества множества атрибутов отношения R. Тогда правила вывода Армстронга определяются следующим образом: 1. Правило рефлексивности: если B является подмножеством множества A, то A B.2. Правило дополнения: если A B, то AC BC. (Здесь запись AC означает объединение множеств A и C).3. Правило транзитивности: если A B и B C, то A C.Каждое из этих правил можно доказать непосредственно на основе определения функциональной зависимости. Из приведенных правил можно вывести несколько дополнительных правил, полезных для практического вычисления замыкания S+. 4. Правило самоопределения: A A.5. Правило декомпозиции: если A BC, то A B и A C.6. Правило объединения: если A B и A C, то A BC.7. Правило композиции: если A B и C D, то AС BD.Кроме того, Дарвен доказал правило, называемое всеобщей теоремой объединения. 8. Если A B и C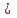 D, то A (С-B) BD.Приведенные правила являются полными в том смысле, что для заданного множества функциональных зависимостей S минимальный набор функциональных зависимостей, которые подразумевают все зависимости из множества S, может выведен из функциональных зависимостей множества S на основе этих правил. Они также являются исчерпывающими, поскольку никакие дополнительные функциональные зависимости с их помощью не могут быть выведены. Иначе говоря, все эти правила могут быть использованы для получения замыкания S+. Пусть задано отношение R и его некоторое множество функциональных зависимостей. Удобнее всего представлять это множество функциональных зависимостей в виде диаграммы функциональных зависимостей. Например диаграмма функциональных зависимостей отношения «Поставщик» представлена на Рис.11.   Имя поставщика        № поставщика адрес поставщика   Статус поставщика  Рис.11. Диаграмма функциональных зависимостей отношения «Поставщик» Каждая стрелка начинается с детерминанта, а ведет к атрибутам зависимой части отношения. 5.2. Суть процесса нормализации Реляционная схема отношений содержит как структурную, так и семантическую информацию. Структурная информация связана с объявлением отношения, а семантическая выражается множеством известных функциональных зависимостей между атрибутами отношений. Однако некоторые функциональные зависимости могут быть нежелательными из-за побочных эффектов или аномалий, которые они вызывают при модификации базы данных. В связи с этим возникает вопрос о корректности представленной схемы отношений. Корректной считается схема отношений, в которой отсутствуют нежелательные функциональные зависимости. В противном случае приходится прибегать к процедуре, называемой декомпозицией (разложением), при которой данное множество отношений заменяется другим множеством отношений, являющихся проекциями первых. Цель этой процедуры – устранение нежелательных функциональных зависимостей, а, значит, аномалий операций обновления данных. В этом заключается суть процесса нормализации. Иначе говоря, нормализация – это пошаговый обратимый процесс замены данной схемы (совокупности) отношений другой схемой, в которой эти отношения имеют более простую, регулярную форму. В теории нормальных форм определяются различные нормальные формы, которые ограничивают типы допустимых функциональных зависимостей. 5.3. Нормальные формы Нормализация – это формальный метод анализа отношений на основе их первичного ключа (или потенциальных ключей) и существующих функциональных зависимостей. Нормализация включает ряд правил, которые могут использоваться для проверки отдельных отношений таким образом, чтобы вся база данных могла быть нормализована до желаемой степени. Если некоторое требование не удовлетворяется, то нарушающее данное требование отношение должно быть декомпозировано на отношения, каждое из которых (в отдельности) удовлетворяет всем требованиям нормализации.         4НФ НФБК 3НФ 2НФ 1НФ Нормализация осуществляется в несколько последовательно выполняющихся этапов, каждый из которых соответствует некоторой нормальной форме, обладающей известными свойствами. В ходе нормализации структура отношений становится все более строгой и менее уязвимой по отношению к аномалиям обновления. Схема взаимосвязей между отдельными нормальными формами приведена на Рис. 10.   5НФ Высшие нормальные формы Рис. 10. Уровни нормализации Из схемы следует, что все нормализованные отношения находятся в 1НФ, некоторые из них также находятся в 2НФ, а некоторые отношения в 2НФ также находятся в 3НФ и т.д. Первые три нормальные формы (1НФ, 2НФ, 3НФ) были предложены Коддом (Codd), в определении последующих принимали также участие Бойс (Boyce) (НФБК) и Фейгин (Fagin) (4НФ, 5НФ). 5.3.1. Первая нормальная форма (1НФ) Отношение находится в 1НФ, если значения всех его атрибутов простые, атомарные, т.е. не являются множеством или повторяющейся группой. При проектировании осуществляется преобразования данных из формата источника в формат ненормализованной таблицы. Ненормализованной таблицей является таблица, содержащая повторяющиеся группы данных. Повторяющейся группой называется группа, состоящая из одного или более атрибутов таблицы, в которой возможно наличие нескольких значений для единственного значения ключа. Например, ненормализованной является таблица Табл.4.
Табл.4. Ненормализованная таблица «Рейсы» Существует простой способ приведения ненормализованной таблицы к 1НФ путем «размножения» значений атрибутов, т.е. ввода данных в каждую строку и каждый столбец отношения. В результате в полученное отношение вносится некоторая избыточность данных, которая в ходе дальнейшей нормализации будет устранена. Результат приведения отношения «Рейсы» к 1НФ отражен в Табл.5.
Табл.5. Нормализованная таблица «Рейсы» (1НФ) 5.3.2. Вторая нормальная форма (2НФ) Вторая нормальная форма (2НФ) основана на понятии полной функциональной зависимости. В некотором отношении множество атрибутов В называется полностью функционально зависимым от множества атрибутов А, если множество В функционально зависит от полного значения множества А и не зависит ни от какого подмножества значений атрибутов А. Отношение является отношением во 2НФ, если оно находится в первой нормальной форме и каждый неключевой атрибут функционально полно зависит от первичного ключа. Рассмотрим пример отношения «Поставки», приведенного в Табл.6.
Табл. 6. Отношение «Поставки»     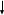 № поставщика Товар Известно, что поставщики могут поставлять разные товары, при этом один и тот же товар могут поставлять разные поставщики. Цена на один и тот же товар фиксирована. Семантические ограничения можно отразить при помощи функциональных зависимостей. Представим их диаграммой функциональных зависимостей, приведенной на Рис. 11. Цена Рис.11. Диаграмма функциональных зависимостей отношения «Поставки» В этом отношении первичным ключом является комбинация атрибутов «№ поставщика», «Товар». Очевидно, что в отношении «Поставки» имеет место неполная функциональная зависимость атрибута «Цена» от первичного ключа, поскольку атрибут «Цена» зависит только от атрибута «Товар». В отношении «Поставки» имеют место аномалии, выявляемые при выполнении операций манипулирования данными: добавления – при добавлении данных о поставке некоторым поставщиком товара, необходимо указать фиксированную цену товара; обновления – если меняется цена на некий товар, необходимо просмотреть все кортежи отношения, поскольку один и тот же товар может поставляться многими поставщиками; удаления – при удалении кортежа с некоторой поставкой можно потерять информацию о цене товара, если этот товар поставлялся единственным поставщиком. Очевидной причиной аномалий в отношении является неполная функциональная зависимость атрибута «Цена» от первичного ключа. Чтобы привести отношение «Поставки» ко 2НФ необходима декомпозиция на два отношения, приведенные на Рис 12. Функциональные зависимости, описанные диаграммой (Рис. 11), очевидно, сохранены. Т.е. декомпозиция выполнена без потерь. Каждое полученное отношение находится во 2НФ, поскольку первичные ключи в отношении – простые. |