Решение экономических задач с помощью методов линейного программирования.

• Название: Решение экономических задач с помощью методов линейного программирования.
• Дата: 16.02.2023
• Размер: 36.75 Kb.
• Имя файла: VKR_zapiska.docx
• Тип: Решение; #941148

Оглавление

Введение 3

Глава 1: Решение экономических задач с помощью методов линейного программирования. 4

1.1Основные понятия линейного программирования 4

1.2 Графический метод и пример с экономическим содержанием 6

1.3 Симплекс метод и пример с экономическим содержанием 6

1.4 Двойственные задачи линейного программирования и пример 6

Список использованных источников 7

Введение

Глава 1: Решение экономических задач с помощью методов линейного программирования.

1. Основные понятия линейного программирования

Линейное программирование – это математический численный метод для оптимизации моделей, в которых целевые функции и ограничения строго являются уравнениями линейной алгебры.^[1] Модель линейного программирования включает целевую функцию, ограничения в виде линейных уравнений или неравенств и требование неотрицательности переменных.^[2] Термин был предложен Дж. Данцигу Т. Купмансом в 1951 году.^[3] Метод применим в военной и экономической логистике для оптимизации доставки грузов и технологических процессов. Был расширен и далее исследован в пору Второй Мировой войны и после.^[3]

Другими словами – линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием.

Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующих систему ограничений, которая имеет, как правило, бесконечное множество решений. Каждая совокупность значений переменных (аргументов функции F), которые удовлетворяют системе ограничений, называется допустимым планом задачи линейного программирования. Функция F, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции F, называется оптимальным планом задачи.

Система ограничений, определяющая множество планов, диктуется условиями производства. Задачей линейного программирования является выбор из множества допустимых планов наиболее выгодного (оптимального).

В общей постановке задача линейного программирования выглядит следующим образом:

Имеются какие-то переменные х = (х₁, х₂ , … х_n ) и функция этих переменных f(x) = f (х₁, х₂ , … х_n ), которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции f(x) при условии, что переменные x принадлежат некоторой области G:



Общая задача линейного программирования имеет вид: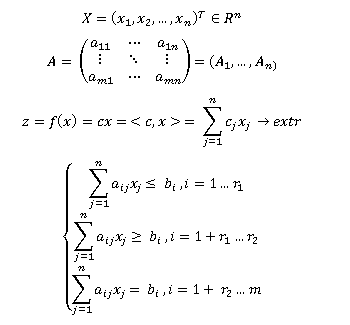



В зависимости от вида функции f(x) и области G и различают разделы математического программирования:

• 
  квадратичное программирование;
  
• 
  выпуклое программирование;
  
• 
  целочисленное программирование и т.д.
  

Линейное программирование характеризуется тем, что:

1. 
   Функция f(x) является линейной функцией переменных х1 , х2 , … хn.
   
2. 
   Область G определяется системой линейных равенств или неравенств.
   

Математическая модель любой задачи линейного программирования включает в себя:

• 
  максимум или минимум целевой функции (критерий оптимальности);
  
• 
  систему ограничений в форме линейных уравнений и неравенств;
  
• 
  требование неотрицательности переменных.
  

Точка называется угловой точкой, если представление , где возможно только при .

Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит (т.е. – не внутренняя точка).

Каноническая форма задачи линейного программирования: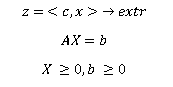



Любая задача линейного программирования сводится к канонической.

Алгоритм перехода от произвольной задачи линейного программирования к канонической форме:

1. 
   Неравенства с отрицательными умножаем на (-1).
   
2. 
   Если неравенство вида (≤), то к левой части добавляем – добавочную переменную, и получаем равенство.
   
3. 
   Если неравенство вида (≥), то из левой части вычитаем , и получаем равенство.
   
4. 
   Делаем замену переменных:
   

• 
  Если , то ;
  
• 
  Если – любой, то , где
  

1.2 Графический метод и пример с экономическим содержанием

1.3 Симплекс метод и пример с экономическим содержанием

Симплекс-метод позволяет эффективно найти оптимальное решение, избегая простой перебор всех возможных угловых точек. Основной принцип метода: вычисления начинаются с какого-то «стартового» базисного решения, а затем ведется поиск решений, «улучшающих» значение целевой функции. Это возможно только в том случае, если возрастание какой-то переменной приведет к увеличению значения функционала.

Необходимые условия для применения симплекс-метода:
Задача должна иметь каноническую форму.

У задачи должен быть явно выделенный базис.

1.4 Двойственные задачи линейного программирования и пример

Список использованных источников

1. 
   Таха Х. Введение в исследование операций 7-е изд. Вильямс, 2005
   
2. 
   http://emm.ostu.ru/lect/lect2.html
   
3. 
   Данциг Д. Линейное программирование, его применения и обобщения (1966).