Аналитическая геометрия
 Скачать 32.58 Kb. Скачать 32.58 Kb.
|
|
Аналитическая геометрия Аналитическая геометрия изучает геометрические объекты по их уравнениям. MS Excel предоставляет широкие возможности визуализации различных уравнений. В Excel наиболее удобно осуществлять построение кривых на плоскости и поверхностей в пространстве. Декартова система координат Для описания точек геометрических объектов с помощью чисел и написания уравнений задают систему координат. Существуют различные системы координат: декартова, полярная, криволинейная и другие. Будем рассматривать наиболее употребительную — декартовую систему координат на плоскости. Декартова система координат может быть прямоугольной и косоугольной. В дальнейшем будем рассматривать декартову прямоугольную систему. На плоскости это две взаимно перпендикулярные числовые оси (рис. 1.1).  Рис. 1.1. Декартова система координат на плоскости Декартовыми координатами точки на плоскости называется упорядоченная пара чисел, являющихся проекциями точки на оси координат. Запись: М(х; у), где х — первая координата, абсцисса, у —вторая координата, ордината. Декартова прямоугольная система координат в пространстве — это три взаимно перпендикулярные числовые оси (рис. 1.2). 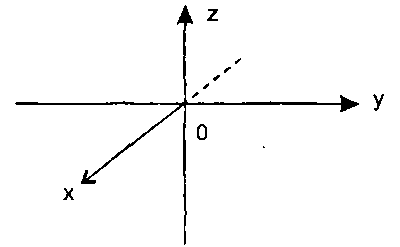 Рис. 1.2. Декартова система координат в пространстве Декартовыми координатами точки в пространстве называется упорядоченная тройка чисел, являющихся проекциями точки на оси координат. Запись: М(х; у; z), где х — абсцисса, у — ордината, z — аппликата. Линии на плоскости Уравнением линии на плоскости Оху называются уравнения F(x,у) = 0 или у = f(х), которым удовлетворяют координаты х и у любой точки, лежащей на линии и не удовлетворяют координаты всякой точки не лежащей на ней. Если дано уравнение, то можно сказать, что линия, определенная уравнением в некоторой системе координат, это геометрическое место точек (ГМТ), координаты которых удовлетворяют уравнению. Уравнение прямой на плоскости в декартовых координатах может записываться по-разному, в зависимости от условий. 1. Уравнение прямой с угловым коэффициентом у = kx + b. Здесь: k = tgα — угловой коэффициент прямой, α — угол наклона прямой к оси х, b — ордината точки пересечения прямой с осью у (рис. 1.3). 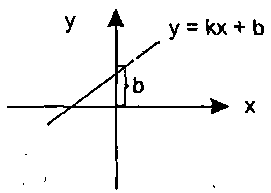 Рис. 1.3. Прямая в декартовых координатах 2. Уравнение прямой, проходящей через данную точку (х1; y1) в данном направлении (с данным углом наклона к оси х) у - y1, = k(x - х1). 3. Уравнение прямой, проходящей через две данные точки (х1; y1) и (х2; у2). 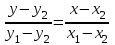 . .4. Уравнение прямой «в отрезках» (рис. 1.4). 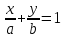 . . Рис. 1.4. Прямая, отсекающая на осях отрезки a и b 5. Общее уравнение прямой: Ах + By + С = 0. Упражнения 1. Построить прямую параллельную оси абсцисс (Ох) и пересекающую ось ординат (Оу) в точке A(0; 2) в диапазоне х € [-3; 3] с шагом Δ = 0,5. 2. Построить биссектрису I—III координатных углов декартовой системы координат в диапазоне х € [-3; 3] с шагом Δ = 0,5. 3. Построить прямую 3х + 2у - 4 = 0 в диапазоне х € [-1; 3] с шагом Δ = 0,25. 4. Построить прямую, пересекающую ось ординат в точке A(0; 2), а ось абсцисс в точке В(3; 0), в диапазоне х € [-1; 4] с шагом Δ = 0,25. 5. Построить прямую, проходящую через начало координат и точку A(2; 3), в диапазоне х € [-1; 4] с шагом Δ = 0,25. 6. Построить прямую, проходящую через точки A(0; 3) и В(2; 2) в диапазоне х € [-1; 4] с шагом Δ = 0,25. 7. Построить прямую с условным коэффициентом а = 3/5 и проходящей через точку К(-1; 2) в диапазоне х € [-1; 3] с шагом Δ = 0,25. 8. Построить прямую, проходящую через две данные точки: М(3; -7) и N(-2; 4) в диапазоне х € [-3; 3] с шагом Δ = 0,25. 9. Построить прямую, заданную общим уравнением: ℓ:3х-5y+15 = 0в диапазоне х € [-1; 3] с шагом Δ = 0,25. 10. Построить прямую, проходящую через точку A(2; -4), параллельно прямой ℓ: 2х-3y + 1 = 0в диапазоне х € [-1; 3] с шагом Δ = 0,25. Даны точки A(-4; 0), B(1; -3), С(4; -2). Построить прямую ℓ, проходящую через А и параллельно ВС в диапазоне х € [-1; 3] с шагом Δ = 0,25. |
