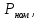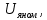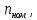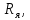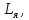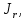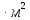Лаба 1. Цель работы Синтез двухконтурной замкнутой сау частотой вращения двигателя постоянного тока независимого возбуждения (дпт нв) серии 2П с каскадным включением регуляторов при постоянстве магнитного потока и приведённого к валу момента инерции нагрузки,
 Скачать 387.37 Kb. Скачать 387.37 Kb.
|
|
Цель работы: Синтез двухконтурной замкнутой САУ частотой вращения двигателя постоянного тока независимого возбуждения (ДПТ НВ) серии 2П с каскадным включением регуляторов при постоянстве магнитного потока и приведённого к валу момента инерции нагрузки, а также исследование динамических режимов работы электропривода методом цифрового моделирования. Исходные данные: Таблица 1. Параметры ДПТ НВ единой серии 2П.
  1. Исследование динамических режимов математической модели ДПТ НВ методом цифрового моделирования. Математическая модель ДПТ НВ имеет следующий вид:  или 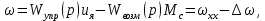 где  - электромеханическая постоянная времени, (с); - электромеханическая постоянная времени, (с);  - электромагнитная постоянная времени, (с); - электромагнитная постоянная времени, (с); 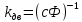 - коэффициент передачи по управляющему воздействию, - коэффициент передачи по управляющему воздействию, 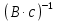 ; ;  - коэффициент передачи по возмущающему воздействию, - коэффициент передачи по возмущающему воздействию, 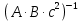 . .Определим численные значения параметров и переменных линеаризованной математической модели ДПТ НВ в номинальном режиме работы.  , ,  , , 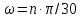 , , 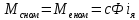 . .  Рис. 1. Численные значения параметров и переменных математической модели ДПТ НВ в номинальном режиме. Методом цифрового моделирования получим временную зависимость изменения угловой скорости вала электрической машины при прямом пуске с 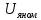 и последующим скачкообразным приложением номинального и последующим скачкообразным приложением номинального  при помощи укрупнённой структурной схемы (рис. 2.). при помощи укрупнённой структурной схемы (рис. 2.).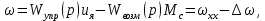 где 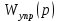 , , 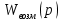 - передаточные функции ДПТ НВ по управляющему и возмущающему воздействиям относительно выхода - передаточные функции ДПТ НВ по управляющему и возмущающему воздействиям относительно выхода 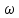 ; ;  , , 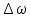 - соответственно динамические значения угловой скорости холостого хода и просадки скорости под действием приведённого момента сопротивления. - соответственно динамические значения угловой скорости холостого хода и просадки скорости под действием приведённого момента сопротивления.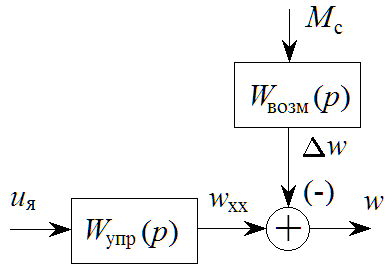 Рис. 2. Укрупнённая схема ДПТ НВ по управляющему и возмущающему воздействиям. Р  ис. 3. Схема набора в MatLab математической модели ДПТ НВ по управляющему и возмущающему воздействиям. ис. 3. Схема набора в MatLab математической модели ДПТ НВ по управляющему и возмущающему воздействиям. Р 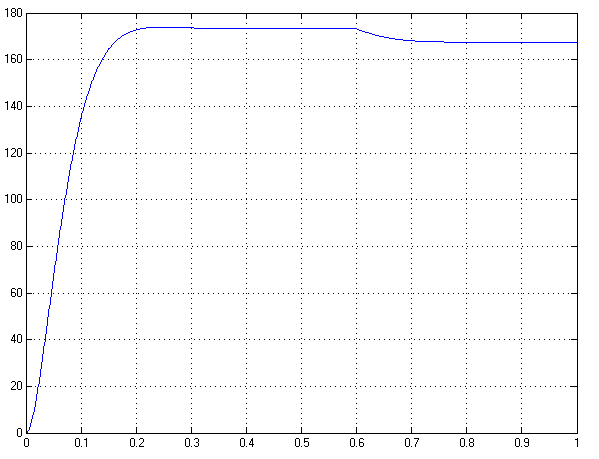 ис. 4. Переходной процесс изменения скорости вала электрической машины при прямом пуске с номинальным напряжением якоря и последующим скачкообразным приложением номинального момента сопротивления. ис. 4. Переходной процесс изменения скорости вала электрической машины при прямом пуске с номинальным напряжением якоря и последующим скачкообразным приложением номинального момента сопротивления.Установившееся значение скорости вала под действием нагрузки, рассчитанное теоретически, совпадает со значением, найденным методом цифрового моделирования. Получим методом цифрового моделирования график изменения угловой скорости вала и тока якоря ДПТ НВ при прямом пуске с 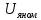 и последующим скачкообразным приложением номинального момента сопротивления при помощи полной структурной схемы ДПТ НВ с координатами состояния и последующим скачкообразным приложением номинального момента сопротивления при помощи полной структурной схемы ДПТ НВ с координатами состояния 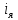 и и 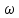 (рис. 5.). (рис. 5.). Рис. 5. Схема набора в MatLab полной математической модели ДПТ НВ. 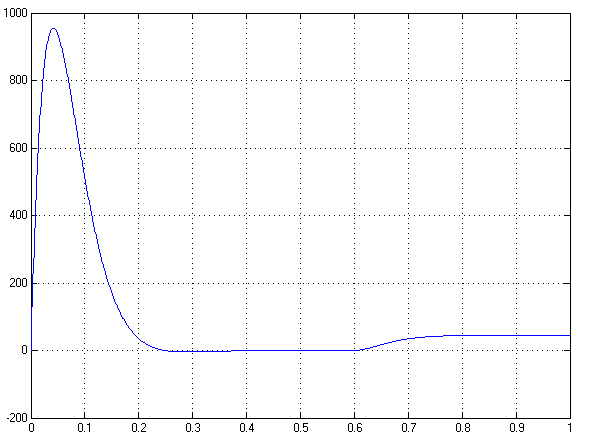 Для скорости вала получаем такой же переходной процесс, как в первом случае (рис. 4.). Следовательно, получаем одинаковые установившиеся значения скорости вала электрической машины. Для скорости вала получаем такой же переходной процесс, как в первом случае (рис. 4.). Следовательно, получаем одинаковые установившиеся значения скорости вала электрической машины. Рис. 6. Переходной процесс изменения тока якоря электрической машины при прямом пуске с номинальным напряжением якоря и последующим скачкообразным приложением номинального момента сопротивления. Значения тока якоря и скорости вала электрической машины, подсчитанные теоретически, совпадают с экспериментальными значениями, найденными методом цифрового моделирования. 2. Синтез внутреннего контура регулирования тока якоря ДПТ НВ при настройке на технический оптимум. Определим структуру и параметры регулятора тока якоря при настройке контура в разомкнутом состоянии на оптимум по модулю. Р 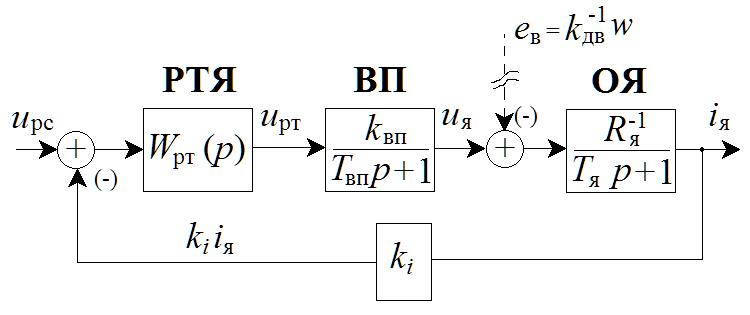 ис. 7. Структурная схема регулирования тока якоря в замкнутом состоянии. ис. 7. Структурная схема регулирования тока якоря в замкнутом состоянии.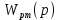 - передаточная функция регулятора тока якоря; - передаточная функция регулятора тока якоря;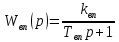 - передаточная функция вентильного преобразователя, где - передаточная функция вентильного преобразователя, где 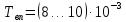 - постоянная времени, (с); - постоянная времени, (с);  - коэффициент передачи, (о.е.). - коэффициент передачи, (о.е.). , ( , ( ), ), 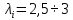 - перегрузочная способность ДПТ НВ по току, при которой обеспечивается безопасная работа коллекторно-щёточного узла. - перегрузочная способность ДПТ НВ по току, при которой обеспечивается безопасная работа коллекторно-щёточного узла.Определяем параметры регулятора тока якоря (рис. 1.). 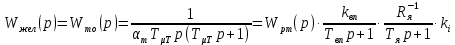 Т. к.  , то в качестве «малой» некомпенсируемой постоянной времени принимаем постоянную времени вентильного преобразователя, т. е. , то в качестве «малой» некомпенсируемой постоянной времени принимаем постоянную времени вентильного преобразователя, т. е.  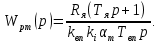 Методом цифрового моделирования получим переходной процесс по 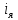 во внутреннем контуре регулирования для случая номинальной нагрузки и определим прямые показатели качества. во внутреннем контуре регулирования для случая номинальной нагрузки и определим прямые показатели качества.Р 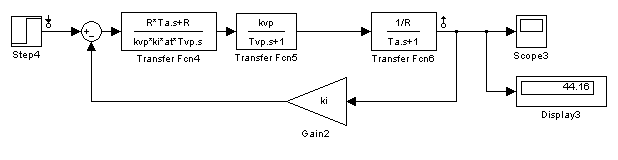  ис. 8. Схема набора в MatLab контура регулирования тока якоря. ис. 8. Схема набора в MatLab контура регулирования тока якоря.Рис. 9. Переходная характеристика тока якоря во внутреннем контуре регулирования и прямые показатели качества переходного процесса.  , ,  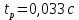 , , 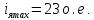 , , 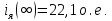 Сравним прямые показатели качества, полученные экспериментально с теоретическими данными: 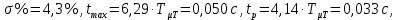 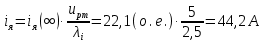 . .Видно, что теоретические прямые показатели качества переходного процесса совпадают с практическими. 3. Синтез внешнего контура регулирования частоты вращения ДПТ НВ при настройке на симметричный оптимум. Синтезируем последовательное корректирующее устройство контура регулирования частоты вращения при его настройке на симметричный оптимум. В целях упрощения процедуры синтеза аппроксимируем внутренний контур регулирования тока якоря в замкнутом состоянии апериодическим звеном в силу второго порядка малости члена 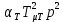 в знаменателе передаточной функции. Тогда в знаменателе передаточной функции. Тогда   Рис. 10. Структурная схема контура регулирования частоты вращения в замкнутом состоянии. 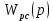 - передаточная функция регулятора частоты вращения. - передаточная функция регулятора частоты вращения.Т. к.  - единственная постоянная времени апериодического звена, то - единственная постоянная времени апериодического звена, то  . .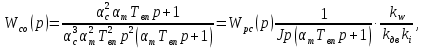 откуда 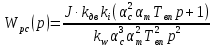 , ,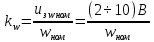 , (В , (В с). с).М 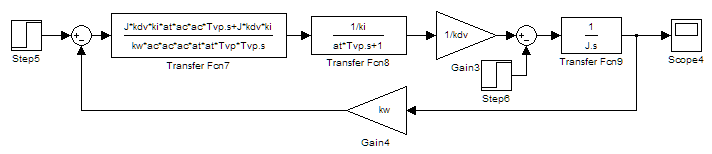 етодом цифрового моделирования получим переходную характеристику по частоте вращения ДПТ НВ в случае аппроксимации контура регулирования тока якоря в замкнутом состоянии апериодическим звеном, а также определим прямые показатели качества переходных процессов по етодом цифрового моделирования получим переходную характеристику по частоте вращения ДПТ НВ в случае аппроксимации контура регулирования тока якоря в замкнутом состоянии апериодическим звеном, а также определим прямые показатели качества переходных процессов по 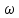 . .Р  ис. 11. Схема набора в MatLab контура регулирования частоты вращения ДПТ НВ. ис. 11. Схема набора в MatLab контура регулирования частоты вращения ДПТ НВ.Рис. 12. Переходная характеристика по частоте вращения ДПТ НВ и прямые показатели качества переходного процесса. 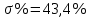 , ,  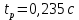 , , 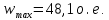 , , 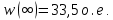 Сравним прямые показатели качества, полученные экспериментально с теоретическими данными: 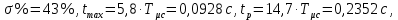 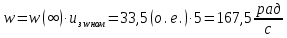 . .Видно, что теоретические прямые показатели качества переходного процесса совпадают с практическими. Методом цифрового моделирования получим переходной процесс по выходу в СПР частоты вращения ДПТ НВ с апериодическим фильтром на входе при прямом пуске с 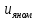 и последующим скачкообразным приложением номинального момента сопротивления. и последующим скачкообразным приложением номинального момента сопротивления.Установим на вход внешнего контура апериодический фильтр с передаточной функцией 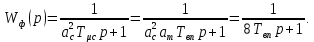 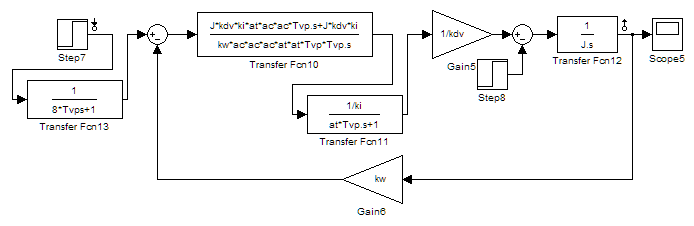 Рис. 13. Схема набора в MatLab контура регулирования частоты вращения ДПТ НВ с апериодическим фильтром на входе. 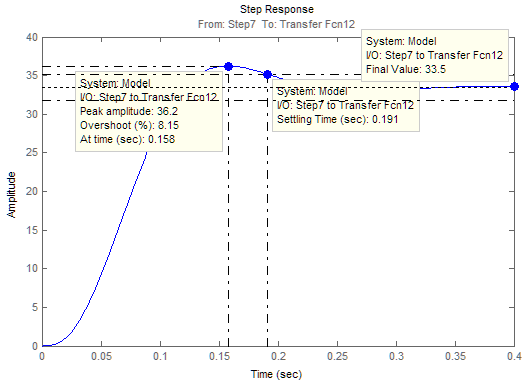 Рис. 14. Переходная характеристика по частоте вращения ДПТ НВ при установке апериодического фильтра на входе контура регулирования частоты вращения ДПТ НВ и прямые показатели качества переходного процесса при прямом пуске с  . .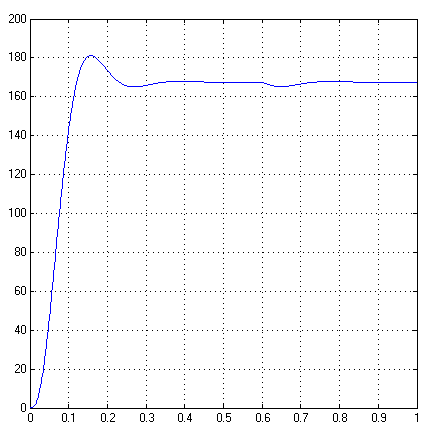 Рис. 15. Переходная характеристика по частоте вращения ДПТ НВ при установке апериодического фильтра на входе контура регулирования частоты вращения ДПТ НВ при прямом пуске с  и последующим скачкообразным приложением номинального момента сопротивления. и последующим скачкообразным приложением номинального момента сопротивления.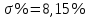 , , 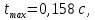  , ,  , , 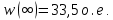 Таким образом, апериодический фильтр позволяет снизить перерегулирование с 43% до 8% и уменьшить время регулирования. Получим переходные процессы по току якоря и частоте вращения, ограничив выходы ПИ-регуляторов частоты вращения РЧВ и тока якоря РТЯ, а также их интегральные составляющие 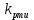 и и 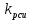 . . , , 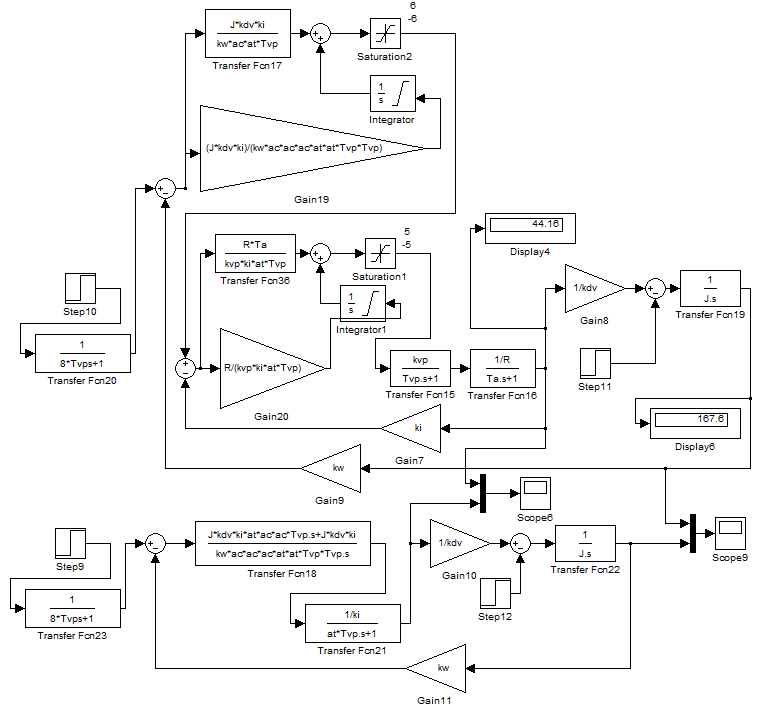 Рис. 16. Схемы набора в MatLab двухконтурных СПР частотой вращения ДПТ НВ с первоначальными и ограниченными составляющими ПИ-регуляторов частоты вращения и тока якоря.  Рис. 17. Переходные процессы по току якоря с первоначальными и ограниченными выходами и интегральными составляющими ПИ-регуляторов частоты вращения и тока якоря. 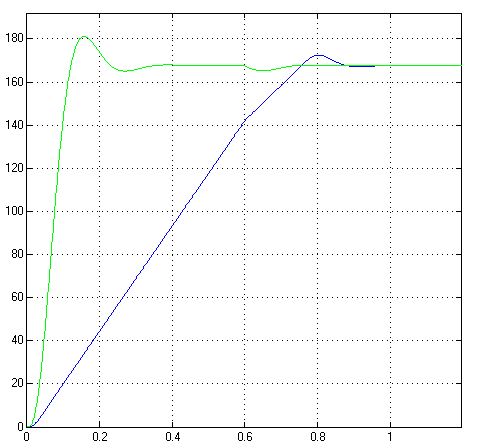 Рис. 18. Переходные процессы по частоте вращения с первоначальными и ограниченными выходами и интегральными составляющими ПИ-регуляторов частоты вращения и тока якоря. При ограничении интегральных составляющих и выходов ПИ-регуляторов частоты вращения и тока якоря в переходном процессе по току якоря скачок тока при пуске не превышает максимально допустимое значение. Таким образом выполняется требование кратковременного максимально допустимого тока якоря, равного трём номинальным токам. В переходном процессе по частоте вращения уменьшилось перерегулирование. Ускорение вала двигателя стало линейным. К  омпенсируем ЭДС вращения: омпенсируем ЭДС вращения:Рис. 19. Схемы набора в MatLab двухконтурных СПР частотой вращения ДПТ НВ с первоначальными и ограниченными составляющими ПИ-регуляторов частоты вращения и тока якоря и с компенсацией ЭДС вращения. 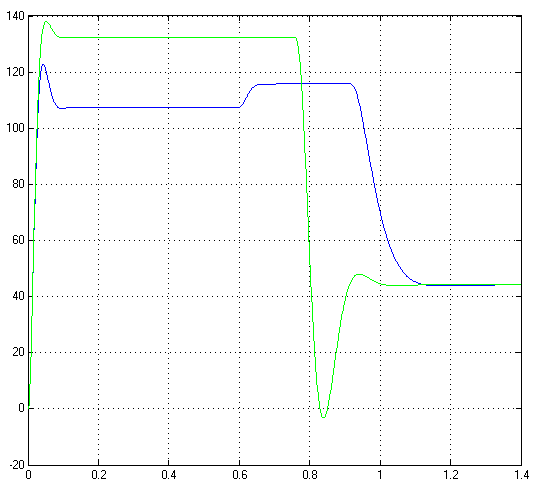 Рис. 20. Переходные процессы по току якоря с первоначальными и ограниченными выходами и интегральными составляющими ПИ-регуляторов частоты вращения и тока якоря в СПР с компенсацией ЭДС вращения. 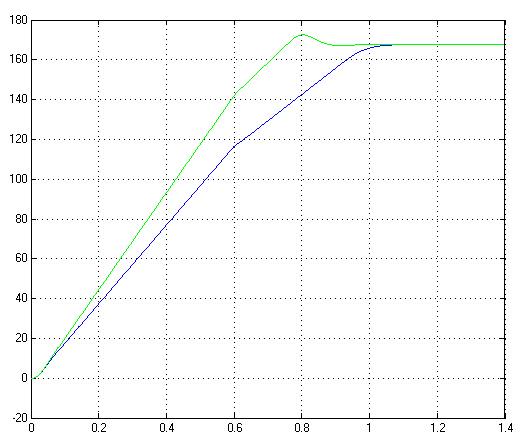 Рис. 21. Переходные процессы по частоте вращения с первоначальными и ограниченными выходами и интегральными составляющими ПИ-регуляторов частоты вращения и тока якоря в СПР с компенсацией ЭДС вращения. При компенсации ЭДС вращения пропадает перерегулирование в переходном процессе по частоте вращения вала двигателя. Ускорение вала становится меньше, двигатель разгоняется плавно. 4. Программа проверки результатов лабораторной работы. 1. Определим по паспортным данным статическое значение просадки угловой скорости 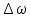 для номинального режима работы, используя следующую формулу для номинального режима работы, используя следующую формулу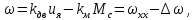 откуда 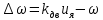 = =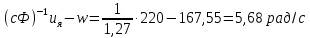 Сравним аналитическое значение просадки скорости со значением, полученным цифровым моделированием. 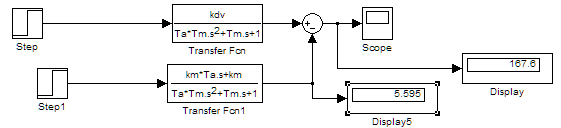 Рис. 22. Схема набора в MatLab математической модели ДПТ НВ по управляющему и возмущающему воздействиям. 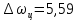 Найдём ошибку моделирования величины 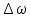 . .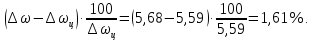 2. Определим текущее значение угловой скорости вала в линеаризованной модели ДПТ НВ при прямом пуске с 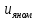 без нагрузки. без нагрузки.Линеаризованная модель ДПТ НВ без нагрузки имеет вид:  т.е. качество переходных процессов определяется характеристическим полиномом колебательного звена   В данном случае  , поэтому имеем пару комплексно-сопряжённых корней с отрицательной вещественной частью, угловая скорость определяется в соответствии с формулой , поэтому имеем пару комплексно-сопряжённых корней с отрицательной вещественной частью, угловая скорость определяется в соответствии с формулой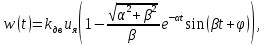 где 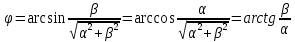 - начальный фазовый сдвиг; - начальный фазовый сдвиг; - соответственно вещественная и мнимая части корней характеристического полинома - соответственно вещественная и мнимая части корней характеристического полинома 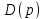 . .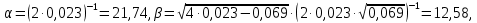 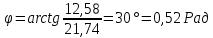 . . Сравним аналитические расчёты со значением, полученным методом цифрового моделирования. 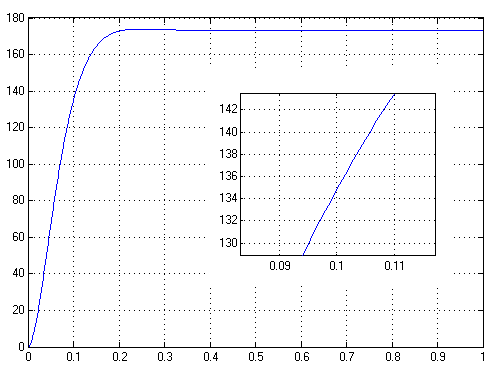 Рис. 23. Значение угловой скорости, полученное методом цифрового моделирования при  . . . .Найдём ошибку моделирования величины 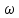 . .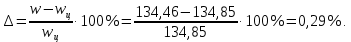 Значение частоты вращения в произвольный момент времени, посчитанное аналитически соответствует значению частоты, найденной методом цифрового моделирования. 3. Определим текущее значение тока якоря во внутреннем контуре регулирования.  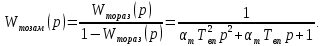 Тогда корни характеристического полинома равны 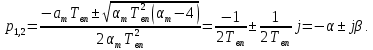 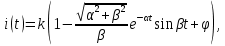 где где 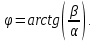 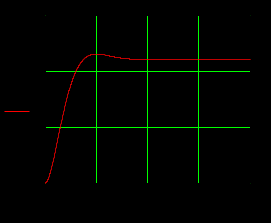 Рис. 24. Расчёты в MathCad и график переходного процесса по току якоря во внутреннем контуре регулирования. 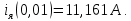 Сравним аналитические расчёты со значением, полученным методом цифрового моделирования.  Рис. 25. Значение тока якоря, полученное методом цифрового моделирования при 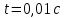 . .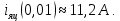 Посчитаем ошибку моделирования: 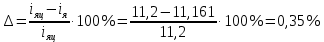 . .Значение тока в произвольный момент времени, посчитанное аналитически соответствует значению тока, найденного методом цифрового моделирования. Выводы: Апериодический фильтр позволяет снизить перерегулирование с 43% до 8% и уменьшить время регулирования скорости вала ДПТ НВ. При ограничении интегральных составляющих и выходов ПИ-регуляторов частоты вращения и тока якоря в переходном процессе по току якоря скачок тока при пуске не превышает максимально допустимое значение. Таким образом выполняется требование кратковременного максимально допустимого тока якоря, равного трём номинальным токам. В переходном процессе по частоте вращения уменьшилось перерегулирование. Ускорение вала двигателя стало линейным. При компенсации ЭДС вращения пропадает перерегулирование в переходном процессе по частоте вращения вала двигателя. Ускорение вала становится меньше, двигатель разгоняется более плавно. |