Лекция 3_Производные высших порядков. Частные производные высших порядков. Экстремумы функции двух переменных
 Скачать 59.37 Kb. Скачать 59.37 Kb.
|
|
. Частные производные высших порядков. Экстремумы функции двух переменных Если частные производные 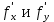 функции z = f (х, у) сами являются дифференцируемыми функциями, то можно найти также и их частные производные, которые называются частными производными второго порядка, то есть функции z = f (х, у) сами являются дифференцируемыми функциями, то можно найти также и их частные производные, которые называются частными производными второго порядка, то есть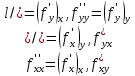 Аналогично определяются частные производные 3-го, 4-го и т.д. порядков. Частная производная второго и более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Имеет место следующая теорема. Теорема Шварца. Если частные производные второго порядка функции z = f (х,у) непрерывны в точке М0(х0,у0), то в этой точке смешанные частные производные равны, то есть 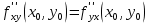 Пример 1. Найти частные производные второго порядка функции  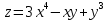 Решение. Так как 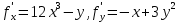 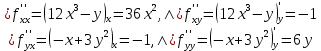 Понятие максимума, минимума, экстремума функции двух переменных аналогичны соответствующим понятиям функции одной переменной. Пусть функция z = f(x, y) определена в некоторой окрестности точки (х0, у0). Точка (х0, у0) называется точкой максимума (минимума) функции z = f (x, y), если существует такая δ - окрестность точки (х0, у0), что во всех ее точках (х,у), отличных от (х0,у0) , выполнятся неравенство 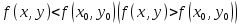 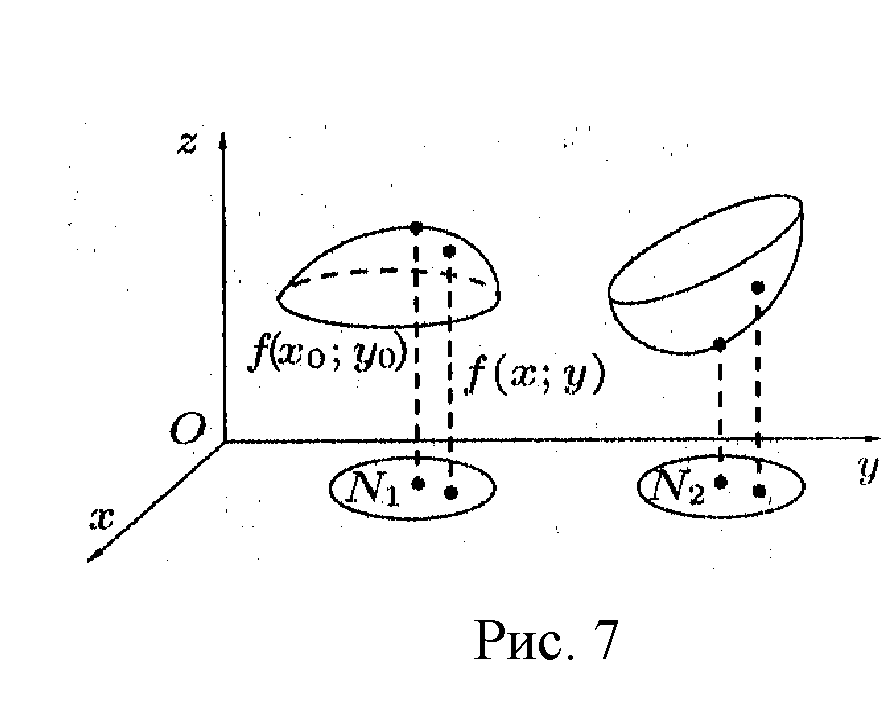 На рисунке 7: N1 - точка максимума, а N2 - точка минимума функции z = f(x, y). Максимум и минимум функции называются ее экстремумами. Теорема (необходимые условия экстремума). Если в точке (х0, у0) дифференцируемая функция z = f (x, y) имеет экстремум, то ее частные производные в этой точке равны нулю: 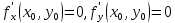 Геометрически равенства 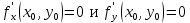 означают, что в точке экстремума функции касательная плоскость к поверхности, изображающей функцию z = f (x, y) , параллельна плоскости Оху , так как уравнение касательной плоскости есть z = z0 . означают, что в точке экстремума функции касательная плоскость к поверхности, изображающей функцию z = f (x, y) , параллельна плоскости Оху , так как уравнение касательной плоскости есть z = z0 .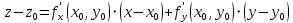 З 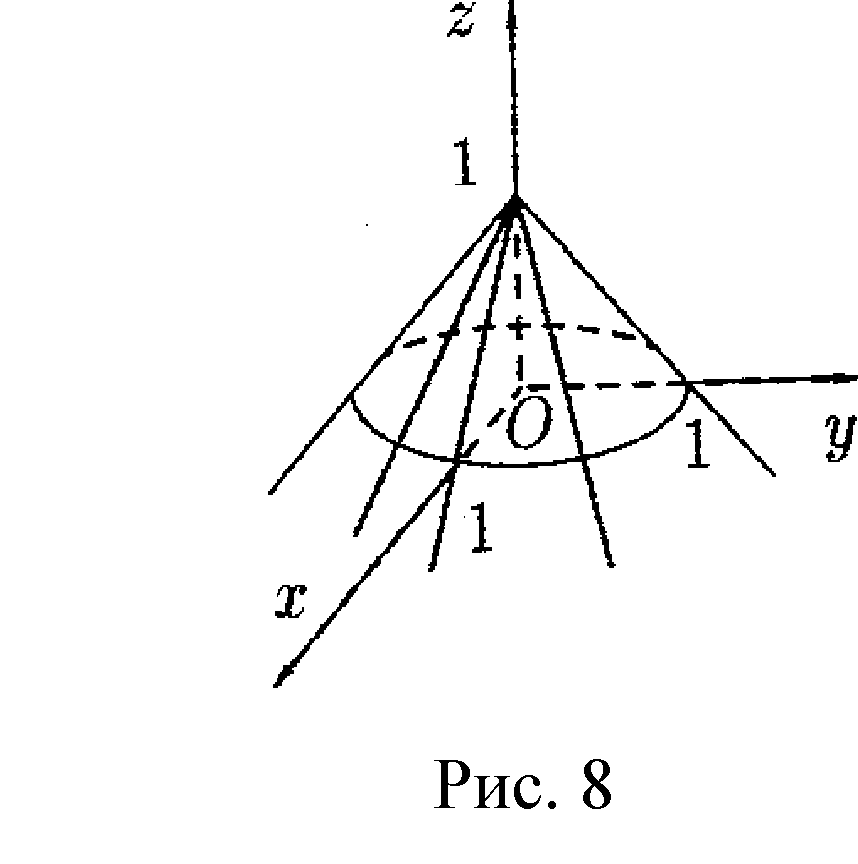 амечание. Функция может иметь экстремум в точках, где хотя бы одна из частных производных не существует. Например, функция амечание. Функция может иметь экстремум в точках, где хотя бы одна из частных производных не существует. Например, функция 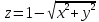 имеет максимум в точке х = 0, у = 0 (см. рис. 8), но не имеет в этой точке частных производных. имеет максимум в точке х = 0, у = 0 (см. рис. 8), но не имеет в этой точке частных производных. Точки, в которой частные производные первого порядка функции z = f (x, y) равны нулю, то есть 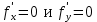 , и точки, в которых хотя бы одна частная производная не существует, называются критическими точками. , и точки, в которых хотя бы одна частная производная не существует, называются критическими точками.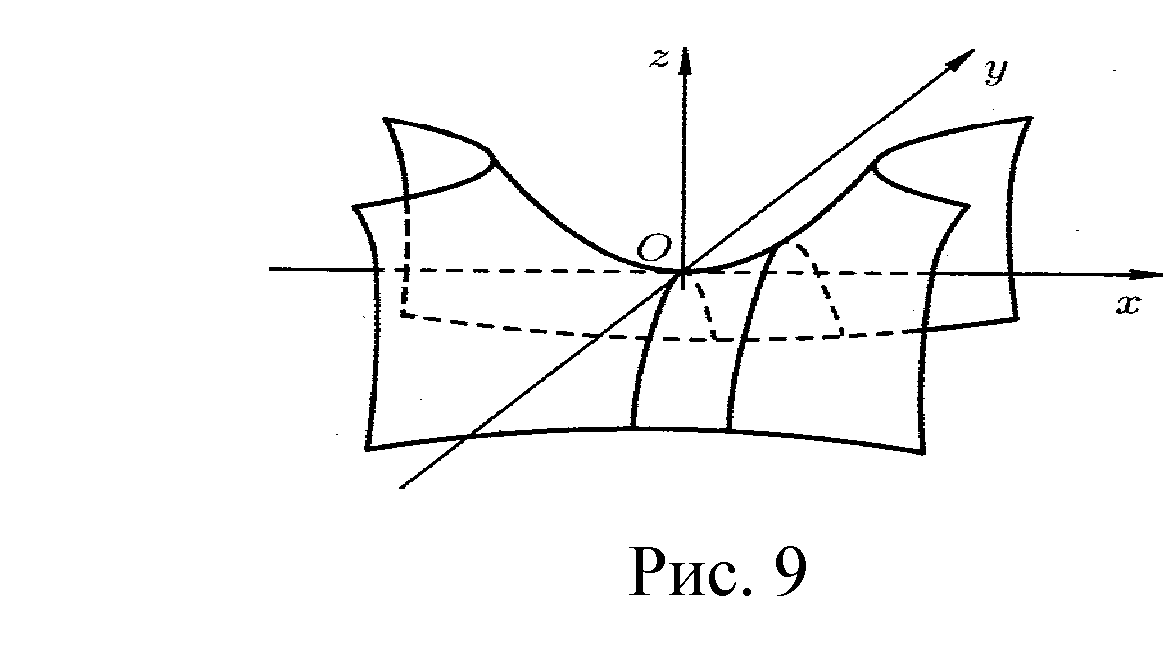 В критических точках функция z = f (x, y) может иметь экстремум, а может и не иметь. Условия В критических точках функция z = f (x, y) может иметь экстремум, а может и не иметь. Условия 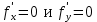 являются необходимыми, но не достаточными условиями существования экстремума. Так, например, для функции z = x2 - y2 точка (0,0) является критической (в ней являются необходимыми, но не достаточными условиями существования экстремума. Так, например, для функции z = x2 - y2 точка (0,0) является критической (в ней 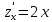 и и 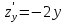 обращаются в ноль), однако, очевидно, никакого экстремума в этой точке нет (см. рис. 9). обращаются в ноль), однако, очевидно, никакого экстремума в этой точке нет (см. рис. 9).Теорема (достаточные условия экстремума). Пусть в некоторой окрестности стационарной точки (х0, у0) функция z = f (x, y) имеет непрерывные частные производные до второго порядка включительно причем 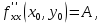 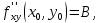 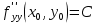 . .Обозначим 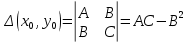 Тогда: 1) если Δ(x0, y0) > 0, то функция z = f (x, y) в точке (х0, у0) имеет экстремум: максимум, если A < 0, и минимум, если A > 0 ; 2) если Δ(x0, y0) < 0, то функция z = f (x,y) в точке (х0, у0) экстремума не имеет; 3) если Δ(x0, y0) = 0, то экстремум в точке (х0, у0) может быть, может не быть. Необходимы дополнительные исследования. Пример 2. Найти точки экстремума функции z = 3x2y- x3 - y4. Решение. 1) Найдем частные производные первого порядка: 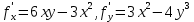 . Точки, в которых частные производные . Точки, в которых частные производные не определены отсутствуют. 2) Найдем стационарные точи, решая систему уравнений: 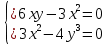 Отсюда получаем две точки: 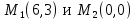 . .3) Находим частные производные второго порядка данной функции: 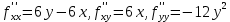 4) В точке М1 (6,3) имеем: A = 6 • 3 - 6 • 6 = -18, B = 6 • 6 = 36, C = -12• 32 =-108, отсюда Δ(6,3) = -18• (-108)-362 = 648 > 0, то есть М1 (6,3) - точка экстремума. Так как A = -18 < 0 , то М1 (6,3) - точка максимума. В точке М2(0,0): A = 0, B = 0, C = 0, отсюда Δ(0,0) = 0. Проведем дополнительное исследование. Значение функции 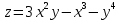 в точке М2 (0,0) равно нулю. Рассмотрим точки из окрестности точки в точке М2 (0,0) равно нулю. Рассмотрим точки из окрестности точки М2(0,0) такие, что х = 0, тогда z(х = 0, у) = -y4 < 0, а теперь рассмотрим точки из той же окрестности, но с условием у = 0 , х < 0 : z(х < 0, у = 0) = -x3 > 0. Таким образом, в любой окрестности точки М2(0,0) функция 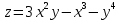 принимает как отрицательные, так и положительные значения. Следовательно, в точке М2 (0,0) функция экстремума не имеет. принимает как отрицательные, так и положительные значения. Следовательно, в точке М2 (0,0) функция экстремума не имеет.10. Наибольшее и наименьшее значение функции в замкнутой области Пусть функция z = f (x, y) определена и непрерывна в ограниченной замкнутой области D. Тогда она достигает в некоторых точках D своего наибольшего и наименьшего значений. Эти значения достигаются функцией в точках, расположенных внутри области D, или в точках, лежащих на границе области. Алгоритм нахождения наибольшего и наименьшего значений дифференцируемой в области D функции z = f(x, y): 1) Найти все критические точки функции, принадлежащие D, и вычислить значения функции в них; 2) Найти наибольшее и наименьшее значения функции z = f (x, y) на границах области; 3) Сравнить все найденные значения функции и выбрать из них наибольшее и наименьшее. П 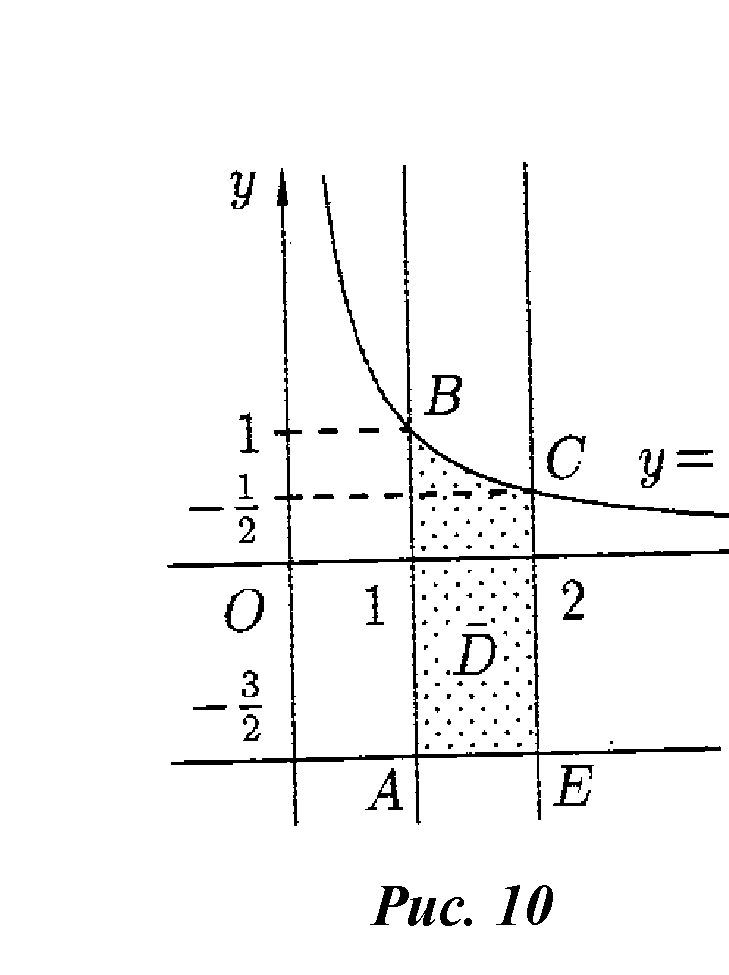 ример 1. Найти наибольшее и наименьшее значение функции ример 1. Найти наибольшее и наименьшее значение функции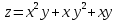 в замкнутой области, ограниченной линиями: в замкнутой области, ограниченной линиями: 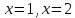 , ,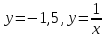 . .Решение. Здесь 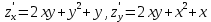 Находим все критические точки: 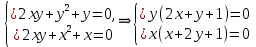 Решением системы являются точки (0,0), (-1,0), (0,-1), 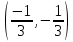 . Ни одна из найденных точек не принадлежит области D. . Ни одна из найденных точек не принадлежит области D.2) Исследуем функцию z = x2y + ху2 + ху на границе области, состоящей из участков АВ , ВС , СЕ и ЕА (см. рис. 10). а) На участке 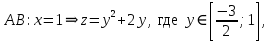 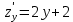 , ,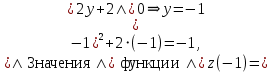 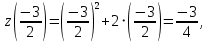 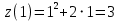 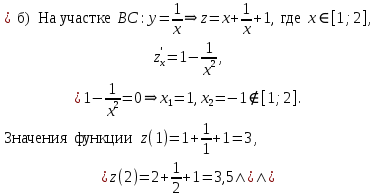 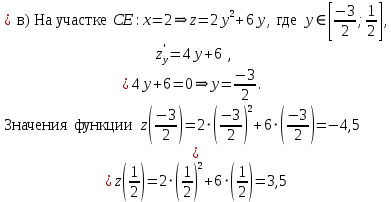 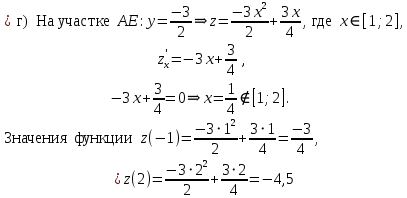 3) Сравнивая полученные результаты, имеем: 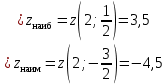 Замечание. Площадь поперечного сечения канала называют его живым сечением, а длину Р границы такого сечения называют смоченным периметром канала. С помощью теоретических расчетов и эксперимента установлено [7], что из всех каналов с заданным живым сечением наибольшей пропускной способностью и одновременно наименьшей фильтрацией отличаются каналы с наименьшим смоченным периметром. Про такие каналы говорят, что они имеют гидравлически наивыгоднейший профиль. Наиболее часто сооружают каналы, а также оросительные и водосточные канавы трапециидальной формы (AB=CD, см. рис. 11). 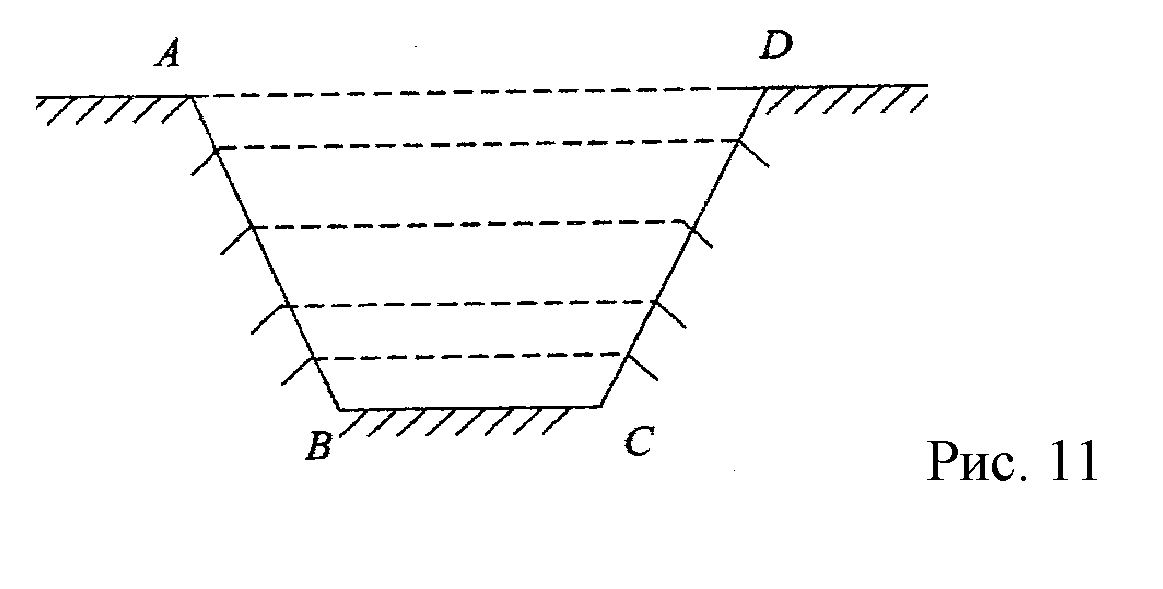 Пример 2. Найти наивыгоднейший с точки зрения гидравлики профиль канала трапецеидальной формы. Решение. Найдем размеры поперечного сечения канала заданной площади S с наименьшим периметром. Пусть AB=CD=y, 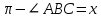 , BC=z. , BC=z.Тогда 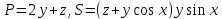 . Выразив z из второй формулы и подставив в первую, получим: . Выразив z из второй формулы и подставив в первую, получим: 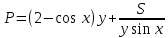 Таким образом, требуется найти такую точку (х0, у0) из области 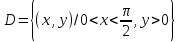 в которой функция Р(х,у) принимает наименьшее значение. в которой функция Р(х,у) принимает наименьшее значение.Найдя частные производные функции Р(х,у) и приравняв их к нулю, получим систему уравнений: 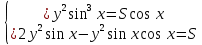 Подставив вместо S в первое уравнение этой системы левую часть второго уравнения, получим 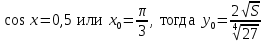 . .В рассматриваемой области D функция P(x,y) имеет единственную критическую точку 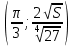 , значение функции в ней равно , значение функции в ней равно 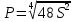 . .Исследуем функцию 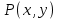 на границе области D: на границе области D: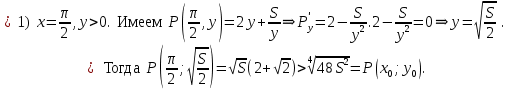 При приближении точки (x, y) к прямым x=0 и y=0, а также при удалении в бесконечность по y функции P(x,y) неограниченно возрастает. Поэтому точку  можно окружить таким прямоугольником можно окружить таким прямоугольником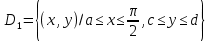 , что вне его и на его границе , что вне его и на его границе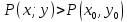 Отсюда следует, что 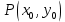 – наименьшее значение функции P(x,y) в области D1, оно же будет наименьшим значением этой функции в области D. – наименьшее значение функции P(x,y) в области D1, оно же будет наименьшим значением этой функции в области D.Итак, функция P(x,y) имеет наименьшее значение 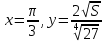 . .Из равенства 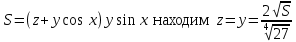 . Таким образов в трапеции . Таким образов в трапеции 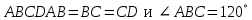 |
