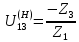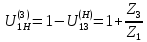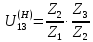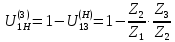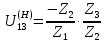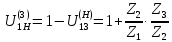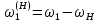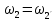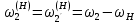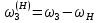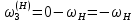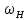Передаточное отношение между двумя колесами. Шпора передаточные. Число внешних зацеплений
 Скачать 214.5 Kb.
|
|
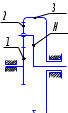
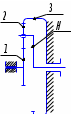
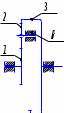
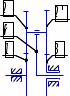
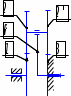
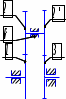
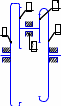
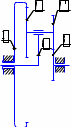
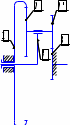
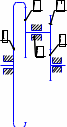
Передаточное отношение между двумя любыми колесами какой угодно зубчатой передачи определяется как отношение угловых скоростей этих колес: 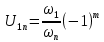 ,где m – число внешних зацеплений. При этом не имеет значения, какое место эти колеса занимают в кинематической цепи, составленной из этих колес. Ввиду того, что определение передаточного отношения зубчатых передач с неподвижными осями вращения не представляет трудностей, в этой работе рассматриваются только дифференциальные и планетарные механизмы, в состав которых входят зубчатые колеса с подвижными осями вращения. Зубчато-рычажные механизмы, степень подвижности которых равна единице, называются планетарными механизмами. Если же степень подвижности механизма превышает единицу, то он называется дифференциальным. В таблице 1 приведены типовые схемы дифференциальных и планетарных механизмов. В этих механизмах колеса, оси которых подвижны, называются сателлитами, а звено, на котором закреплены оси сателлитов, называется водилом и на схемах обычно обозначается буквой H латинского алфавита. Зубчатые колеса с неподвижными осями вращения называются центральными, или солнечными. Неподвижное центральное колесо часто называют опорным. Существуют графический и аналитический методы определения передаточного отношения планетарных и дифференциальных механизмов. В данной работе используется аналитический метод. Он основан на методе Таблица 1
*Примечание: верхний индекс в скобках показывает номер звена, которое является неподвижным. обращения движения, или так называемом методе инверсии, который состоит в следующем: всем звеньям механизма, в том числе и стойке, сообщается дополнительное вращение вокруг оси центральных колес с угловой скоростью ωН, то есть с угловой скоростью, равной и противоположной угловой скорости водила Н. В результате такого приема дифференциальный и планетарный механизмы превращаются в обыкновенные зубчатые механизмы с неподвижными осями. Зубчатый механизм, полученный в результате инверсии, называется обращенным. Передаточное отношение обращенного механизма (табл. 1) между любыми его звеньями можно выразить через угловые скорости колес и водила. Для этой цели используем таблицу 2. Таблица 2
Нумерация звеньев в таблице такая же, как в таблице 1. В качестве примера возьмем любой из дифференциальных механизмов, представленных в таблице 1, и, пользуясь данными таблицы 2, найдем передаточное отношение от центрального колеса 1 к центральному колесу 3 обращенного механизма, выраженное через угловые скорости этих колес и водила при подвижном водиле. Результат будет следующим: 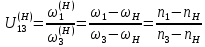 , (1)где 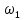 ,  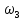,  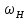– угловые скорости звеньев до сообщения им дополнительного вращения с угловой скоростью 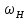.Формула 1 называется формулой Виллиса. Легко заметить, что для всех дифференциальных и планетарных механизмов соответствующие обращенные механизмы различны, а поэтому различны и выраженные через числа зубьев колес передаточные отношения обращенных механизмов. Что же касается передаточных отношений, выраженных через угловые скорости, то они одинаковы для всех типов дифференциальных и планетарных механизмов. В этом универсальность формулы Виллиса. Теперь определим передаточные отношения обращенных механизмов, выраженные через числа зубьев, между центральными колесами 1 и 3 для четырех типовых схем дифференциальных и планетарных механизмов, помещенных в таблицу 1. Для схемы № 1: 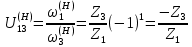 . Для схемы № 2: 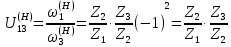 . Для схемы № 3: 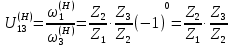 . Для схемы № 4: 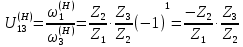 . Таким образом, передаточное отношение 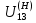 в формуле (1) известно, если известны числа зубьев колес дифференциального механизма. В эту формулу входят угловые скорости трех звеньев, и поэтому, если заданной является угловая скорость только одного звена, то уравнение имеет бесчисленное множество решений, то есть угловые скорости двух других звеньев могут быть любыми, а дифференциальный механизм не будет иметь никакого определенного передаточного отношения. Это объясняется тем, что кинематическая цепь, имеющая две степени свободы, допускает произвольные движения ведомых звеньев. Если же будет задана угловая скорость еще одному звену, тогда степень свободы механизма станет равной единице и уравнение (1) будет иметь однозначное решение. То есть, если заданы угловые скорости двух каких-либо звеньев дифференциального механизма, то угловая скорость третьего звена однозначно определится из уравнения (1), а передаточное отношение дифференциального механизма будет вполне определенным. Так, например, если одному из центральных колес дифференциального механизма задать угловую скорость, равную нулю, то есть сделать его неподвижным, то получим планетарный механизм с одной степенью свободы. 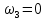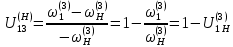Пусть, например,  , тогда формула (1) принимает вид или 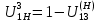 . Передаточное отношение между любыми колесами планетарного механизма можно определить так: 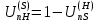 . (2)Передаточное отношение от любого n-го колеса планетарного механизма к водилу при неподвижном опорном колесе 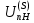 равно единице минус передаточное отношение обращенного механизма от того же n-го колеса к опорному при неподвижном водиле 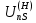 .Приведем несколько примеров. Пример 1. Найти число об/мин водила Н и сателлита 2', если ведущее колесо 1 делает 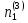 = 900 об/мин. Числа зубьев колес: Z1 = Z2' = 16; Z3 = 64; Z2 = 32. 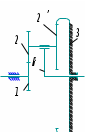Для решения задачи надо найти передаточные отношения от колеса 1 к водилу Н и от водила Н к сателлиту 2-2'. Находим передаточное отношение  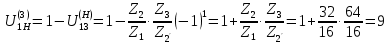 . 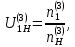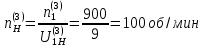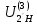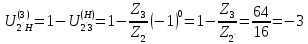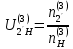Находим число оборотов водила:  откуда  .Находим  от сателлита к водилу:  ,откуда 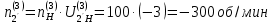 . Следовательно, сателлит 2-2' вращается против вращения водила или, что одно и то же, против ведущего колеса 1. Пример 2. Определить передаточное отношение  редуктора с плавающим водилом, если числа зубьев колес равны: Z1 = 12, Z2' = 48, Z3 = 120, Z4 = 150.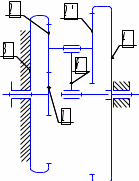 Решение: 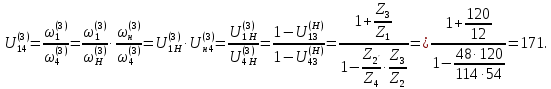 Пример 3. В планетарном механизме ведущее колесо 1 делает 1300 об/мин. Определить число об/мин двух ведомых валов: вала водила Н и вала колеса 3. 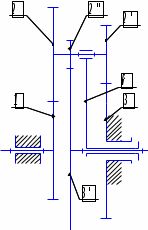 Порядок решения задачи следующий: сначала определим число оборотов водила 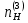 , а затем, приняв водило за ведущее звено в планетарном механизме, в состав которого входят колеса 3', 2'', 2', 3 и водило Н, определим число оборотов вала колеса 3'.Определим число оборотов водила Н из условия, что 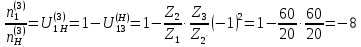 ,тогда 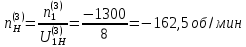 .Теперь, приняв водило за ведущее звено, определим число оборотов колеса 3' и вала, на котором оно сидит. 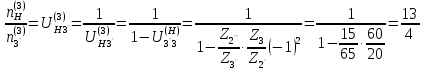 ,тогда 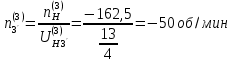 .Знаки минус перед значениям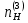и и 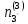 указывают на то, что водило и колесо 3' вращаются в сторону, противоположную вращению колеса 1.В технике нередко применяются зубчато-рычажные механизмы, получившие название «замкнутый дифференциал». Они состоят из дифференциального механизма, между входными звеньями которого установлена связь в виде зубчатой передачи. Обычно эта дополнительная зубчатая передача устанавливается между центральными колесами или между одним из центральных колес и водилом. Приведем пример такого механизма. Пример 4. Определить передаточное отношение 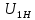 редуктора (замкнутого дифференциала) электрополиспаста, если числа зубьев колес равны: Z1 = 24, Z2 = 52, Z3 = 78, Z3' = 18, Z4 = 30, Z4' = 78.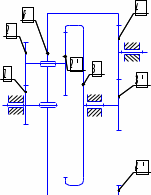 Дополнительную связь здесь представляет передача, составленная из колес 3', 4, 4', которая связывает числа оборотов центрального колеса 3-3' и водила Н. Решение: Согласно формуле Виллиса 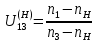 ,кроме того, 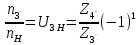 , откуда 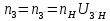 ,тогда, подставив это в формулу Виллиса, получим: 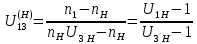 ,откуда   . | |||||||||||||||||||||||||||||||||||||||||||||||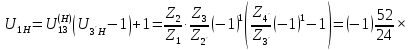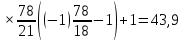
