Динамическое программирование

• Название: Динамическое программирование
• Анкор: 18zada
• Дата: 04.03.2022
• Размер: 0.98 Mb.
• Имя файла: ege18.doc
• Тип: Документы; #382434
• страница: 1 из 7

© К. Поляков, 2018-2021

18 (повышенный уровень, время – 6 мин)

Тема: Динамическое программирование

Что проверяется:

Умение обрабатывать вещественные выражения в электронных таблицах.

3.4.3. Использование инструментов решения статистических и расчётно-графических задач.

1.1.2. Умение представлять и анализировать табличную информацию в виде графиков и диаграмм.

Что нужно знать:

• 
  в задачах, которые предлагаются в этом задании КИМ, нужно найти оптимальный путь для Робота, который перемещается на клетчатом поле. Робот может на каждом шаге выбирать одно из двух направлений движения (например, только вправо и вниз).
  
• 
  в каждой клетке Робот получает некоторую награду («берёт монету»), и нужно найти такой путь, при котором общая награда будет наибольшая (или наименьшая, если это не награда, а штраф)
  
• 
  конечно, теоретически можно решить такую задачу полным перебором вариантов: рассмотреть все возможные пути и выбрать лучший. Однако количество возможных путей для полей даже не очень большого размера слишком велико для того, чтобы решить эту задачу за время проведения ЕГЭ, даже если вам удастся безошибочно написать программу для такого перебора.
  
• 
  эта задача успешно и быстро решается с помощью динамического программирования – метода оптимизации, который предложил американский математик Ричард Беллман. Он сформулировал очень простой принцип оптимальности пути: любая часть оптимального пути оптимальна. Например, пусть мы нашли оптимальный путь из точки А и точку Б, который проходит через точки В, Г и Д: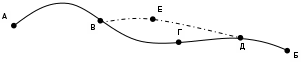
  

Принцип Беллмана утверждает, что, например, путь ВГД – это оптимальный путь из В в Д. Если бы это было не так и существовал бы другой, лучший путь между В и Д (например, ВЕД на рисунке), то и путь АВГДБ не был бы оптимальным.

• 
  рассмотрим применение динамического программирования на простом примере: Робот идёт по клетчатому полю из левого верхнего угла в правый нижний; на каждом шаге он может переместиться на одну клетку вправо или на одну клетку вниз. В каждой клетке лежит заданное количество монет:
  

	A	B	C
1	63	78	58
2	10	1	42
3	25	29	87

Нужно найти такой путь из клетки А1 в клетку С3, пройдя по которому Робот соберёт наибольшее количество монет.

• 
  (Б.С. Михлин) Будем решать задачу со стартовой клетки A1. Исходное количество монет в клетках выделим красным цветом, а старт и финиш - желтой заливкой. Тогда исходная таблица примет следующий вид:
  

	A	B	C
1	63	78	58
2	10	1	42
3	25	29	87

Построим ряд дополнительных таблиц, в которых для каждой клетки будем записывать наибольшее число монет, которое может собрать робот, пройдя из стартовой клетки А1 в очередную клетку по пути к финишной клетке C3. Проходить по таблице будем построчно сверху вниз. Текущую клетку будем выделять жирным шрифтом.

• 
  в стартовой клетке А1 63 монеты и робот их соберёт.
  

  	A	B	C
  1	63
  2
  3

• 
  в B1 робот может попасть только из А1. При этом он в сумме соберет: 63+78=141 монету.
  

  	A	B	C
  1	63	141
  2
  3

• 
  в C1 робот может попасть только из B1. При этом он соберет 141+58=199 монет.
  

  	A	B	C
  1	63	141	199
  2
  3

• 
  в A2 робот может попасть только из А1. При этом он в сумме соберет: 63+10=73 монеты.
  

  	A	B	C
  1	63	141	199
  2	73
  3

• 
  в B2 робот может попасть из A2 и из B1. Чтобы собрать больше монет он будет шагать из B1 и соберет 141+1=142 монеты. (Если бы он шагнул из A2, то собрал бы меньше: 73+1=74 монеты).
  

  	A	B	C
  1	63	141	199
  2	73	142
  3

• 
  в C2 робот может попасть из B2 и из C1. Чтобы собрать больше монет он будет шагать из C1 и соберет: 199+42=241 монету. (Если бы он шагнул из B2, то собрал бы меньше: 142+42=184 монеты).
  

  	A	B	C
  1	63	141	199
  2	73	142	241
  3

• 
  в A3 робот может попасть только из A2. При этом он соберет 73+25=98 монет.
  

  	A	B	C
  1	63	141	199
  2	73	142	241
  3	98

• 
  в B3 робот может попасть из A3 и из B2. Чтобы собрать больше монет он будет шагать из B2 и соберет: 142+29=171 монету. (Если бы он шагнул из A3, то собрал бы меньше: 98+29=127 монет).
  

  	A	B	C
  1	63	141	199
  2	73	142	241
  3	98	171

• 
  в C3 робот может попасть из B3 и из C2. Чтобы собрать больше монет он будет шагать из C2 и соберет: 241+87=328 монет. (Если бы он шагнул из B3, то собрал бы меньше: 171+87=258 монет).
  

	A	B	C
1	63	141	199
2	73	142	241
3	98	171	328

Ответ: 328 монет.

Пример задания:

Р-03 (В.Н. Шубинкин). Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой только в том случае, если её номинал – число, кратное 3; если номинал монеты – число, не кратное 3, то Робот не берёт монету; это также относится к начальной и конечной клетке маршрута Робота. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.

Исходные данные для Робота записаны в файле 18-0.xls в виде электронной таблицы прямоугольной формы.

Решение (электронные таблицы, В.Н. Шубинкин):

1. 
   Решение отличается от решения P-00 использованием дополнительных функций: ЕСЛИ() и ОСТАТ(). Функция ОСТАТ(число;делитель) имеет два аргумента и возвращает остаток от деления значения параметра число на значение параметра делитель, который можно сравнить с 0 для определения кратности числа делителю.
   
2. 
   откроем файл с электронной таблицей размером 10 на 10: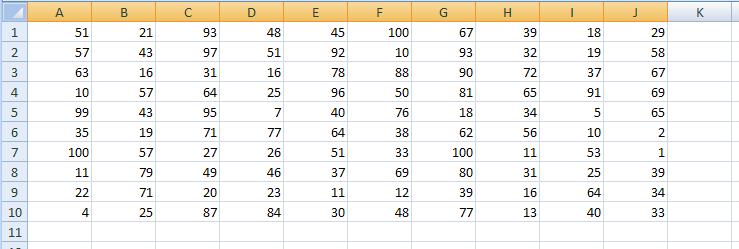
   

Робот начинает движение из верхнего левого угла (из ячейки А1) и перемещается в правый нижний (то есть в J10)

3. 
   при использования метода динамического программирования требуется выделить для вычислений дополнительную таблицу такого же размера; проще всего сделать так:
   

• 
  скопировать исходную таблицу вниз
  
• 
  обвести её рамкой (и/или выделить фоном), чтобы запомнить исходный размер;
  
• 
  стереть все данные в копии.
  

вот что должно получиться: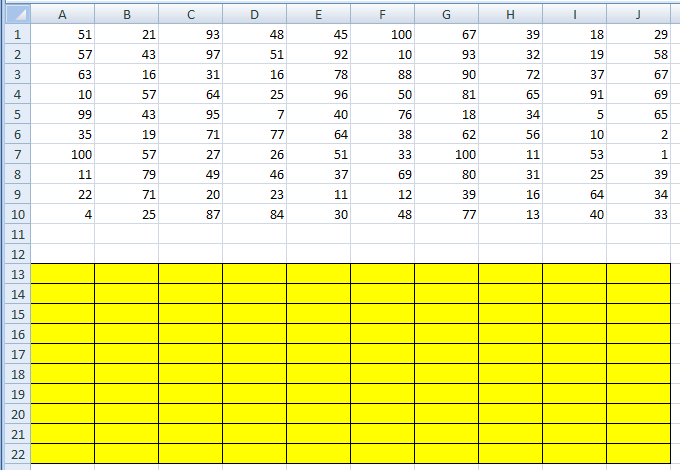

4. 
   дальше мы будем работать только с областью, выделенной жёлтым фоном
   
5. 
   предположим, что робот уже находится в правом нижнем углу; в этом случае он может получить только сумму в этой ячейке, то есть величину J10, НО при условии, что она кратна 3; записываем в J22 формулу =ЕСЛИ(ОСТАТ(J10;3)=0;J10;0).
   

Примечание. Третий аргумент функции ЕСЛИ() можно вообще не указывать. Тогда при ложном улсовииполе останется пустым и при вычислениях будет эквивалентно 0.

После ввода формулы видим в ячейке J22 значение 33, как и ожидалось: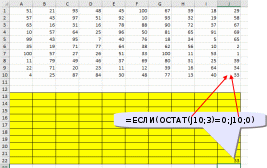

6. 
   рассмотрим нижний ряд: если Робот находится в одной из ячеек последней строки 10, то он может идти только вправо, собирая монеты в последней строке; например, начав движение из ячейки I10 он соберёт монету в этой ячейке, если её номинал кратен 3 и во всех (в данном случае – в одной) следующих (опять же только если номинал монет кратен 3), то есть формула в ячейке I22 должна быть = ЕСЛИ(ОСТАТ(I10;3)=0;I10;0)+J22. В отличие от ячейки J10 значение в ячейке I10 не кратно 3, поэтому наблюдаем, что сумма осталась прежней (33) (то есть, если бы Робот стартовал из ячейки I10, то он набрал бы только 33, так как 40 не делится на 3):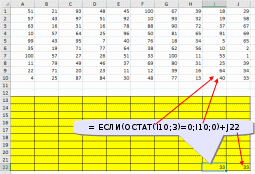
   

7. 
   эту формулу копируем (протаскиваем за маркер заполнения) по всей строке 22: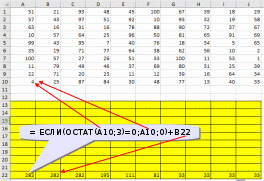
   

8. 
   аналогично если Робот находится в последнем столбце, он может двигаться только вниз, собирая по пути все монеты, номинал которых кратен 3; вводим в ячейку J21 формулу =ЕСЛИ(ОСТАТ(J9;3)=0;J9;0)+J22 и протаскиваем (копируем) её вверх на весь столбец J вспомогательной таблицы: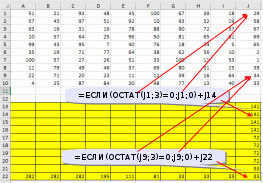
   

9. 
   займёмся центральными ячейками жёлтой таблицы, которые пока не заполнены; пусть Робот находится в ячейке I9; тогда для того, чтобы получить максимальную сумму, ему нужно выбрать лучший из двух путей – пойти в I10 или в J9; из второй таблицы видим, что значения в этих ячейках одинаковы, но тем не менее формулу напишем таким образом, чтобы она правильно работала и для разных значений, ведь мы распространим её на всю оставшуюся часть таблицы с помощью маркера автозаполнения. В формуле нужно выбрать максимум из значений ячеек I10 и J9, получаем =ЕСЛИ(ОСТАТ(I9;3)=0;I9;0)+МАКС(I22;J21); обратите внимание, что оба аргумента функции МАКС находятся в рабочей таблице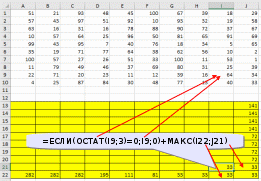
   

10. 
    для всех оставшихся ячеек принцип вычисления максимальной суммы тот же самый: нужно добавить к значению этой ячейки в исходной таблице максимум из накопленных сумм, которые Робот собирает в случае двух возможных шагов; копируем формулу из I21 на весь диапазон A13:I21 (сначала можно растянуть формулу на диапазон-столбец I13:I21, а затем этот диапазон – на нужный диапазон A13:I21)
    

Первый ответ к задаче – это максимальная сумма, накопленная при движении из левого верхнего угла; она записана в левом верхнем углу рабочей таблицы, то есть в ячейке A13 (она выделена зелёным фоном):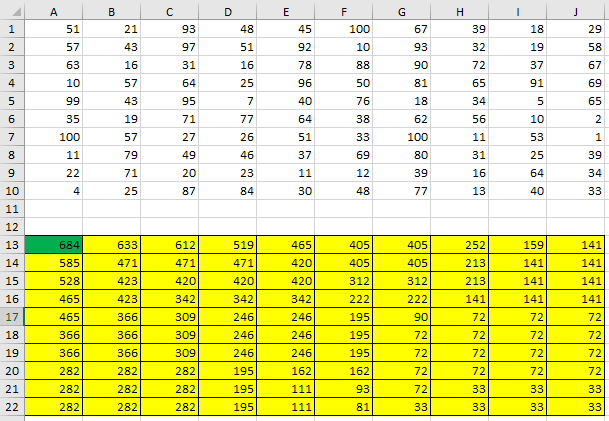

11. 
    чтобы найти наименьшую возможную сумму, нужно в формуле в п. 9 заменить функцию МАКС на МИН: =ЕСЛИ(ОСТАТ(I9;3)=0;I9;0)+МИН(I22;J21)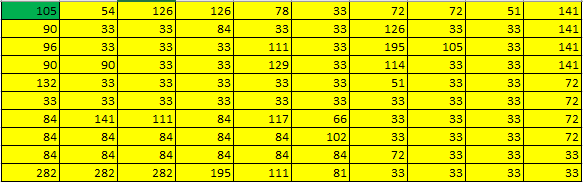
    

12. 
    Ответ: 684 105
    
13. 
    (Б.С. Михлин) При данном условии задачи все равно, в каком направлении двигаться: мы получим тот же результат, если будем рассматривать обратное движение – влево и вверх из правого нижнего угла. Поэтому задачу можно решать, начиная с левого верхнего угла таблицы, при этом ответ получается в правом нижнем углу рабочей области.
    

Ещё пример задания:

Р-02 (А. Кабанов). Дана последовательность натуральных чисел. Рассматриваются всевозможные пары чисел, номера которых i и j в последовательности различаются более чем на 4 (i  j – 4). Определите количество таких пар, для которых сумма чисел чётна. Исходная последовательность записана в виде одной строки электронной таблицы.

Решение (электронные таблицы):

1. 
   Рассмотрим решение на примере следующей таблицы.
   

2. 
   Для определённости будем двигаться справа налево. Для каждого числа a_i рассмотрим набор из предыдущих чисел (кроме последних трёх). Число a_i будет образовывать подходящие пары с числами такой же чётности. Для каждого числа вычислим остаток от деления на 2. В ячейке A2 запишем формулу =ОСТАТ(A1;2) и скопируем её на все остальные ячейки второй строки.
   

3. 
   С помощью формулы СЧЁТЕСЛИ подсчитаем, сколько из предыдущих чисел(кроме последних трёх) имеют такую же чётность. Например, в ячейке K3 формула будет иметь вид =СЧЁТЕСЛИ($A$2:G2;"="&K2). Начало диапазона – абсолютная ссылка для корректного автозаполнения. Формулу запишем в ячейку K3 и скопируем во все ячейки третьей строки. Для первых 4 чисел количество пар равно 0.
   
4. 
   Общее количество равно сумме пар, образуемых каждым числом. В ячейке A4 запишем формулу =СУММ(A3:N3)
   

5. 
   Ответ: 25.
   

Пример задания:

Р-01 (А. Кабанов). Дана последовательность натуральных чисел. Рассматриваются всевозможные пары чисел, номера которых i и j в последовательности различаются не более чем на 5 (i+1  j  i+5). Определите количество таких пар, в которых сумма чисел меньше 100. Исходная последовательность записана в виде одной строки электронной таблицы.

Решение (электронные таблицы):

1. 
   Рассмотрим решение на примере следующей таблицы.
   

2. 
   Для определённости будем двигаться справа налево. Для каждого числа a_i рассмотрим набор из пяти предыдущих чисел (если таковые существуют). Число a_i будет образовывать подходящие пары с числами, меньшими 100 – a_i. С помощью формулы СЧЁТЕСЛИ подсчитаем, сколько из предыдущих пяти чисел меньше 100 – a_i. Например, в ячейке F2 формула будет иметь вид =СЧЁТЕСЛИ(A1:E1;"<"&(100-F1)). Формулу запишем в ячейку F2 и скопируем во все ячейки строки. Для первых 5 чисел формулу необходимо откорректировать.
   

3. 
   Общее количество равно сумме пар, образуемых каждым числом. В ячейке A3 запишем формулу =СУММ(A2:N2)
   

4. 
   Ответ: 9.
   

Ещё пример задания:

Р-00 (демо-2021). Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.

Исходные данные записаны в файле 18-0.xls в виде электронной таблице размером N×N, каждая ячейка которой соответствует клетке квадрата.

Решение (электронные таблицы):

1. 
   откроем электронную таблицу и увидим следующую таблицу размером 10 на 10:
   

Робот начинает движение из верхнего левого угла (из ячейки А1) и перемещается в правый нижний (то есть в J10)

2. 
   при использования метода динамического программирования требуется выделить для вычислений дополнительную таблицу такого же размера; проще всего сделать так:
   

• 
  скопировать исходную таблицу вниз
  
• 
  обвести её рамкой (и/или выделить фоном), чтобы запомнить исходный размер;
  
• 
  стереть все данные в копии.
  

вот что должно получиться:

3. 
   дальше мы будем работать только с областью, выделенной жёлтым фоном
   
4. 
   предположим, что робот уже находится в правом нижнем углу; в этом случае он может получить только сумму в этой ячейке, то есть величину J10; записываем в J22 формулу =J10; после ввода формулы видим в ячейке J22 значение 33, как и ожидалось: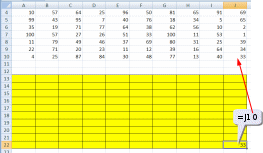
   

5. 
   рассмотрим нижний ряд: если Робот находится в одной из ячеек последней строки 10, то он может идти только вправо, собирая монеты в последней строке; например, начав движение из ячейки I10 он соберёт монету в этой ячейке и во всех (в данном случае – в одной) следующих, то есть формула в ячейке I22 должна быть =I10+J22;
   

обратите внимание, что первая ссылка в формуле (I10) обращается к исходной таблице (берёт из неё одно значение), а вторая (J22) – к рабочей (берёт всё накопленное далее); неудивительно, что в I22 появляется число 73: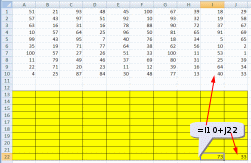

6. 
   эту формулу копируем (протаскиваем за маркер заполнения) по всей строке 22: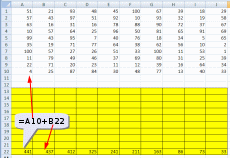
   

здесь хорошо видно, что для того чтобы сумма накапливалась, вторая ссылка в формуле должна указывать на строку 22, а не на строку 10

7. 
   аналогично если Робот находится в последнем столбце, он может двигаться только вниз, собирая по пути все монеты; вводим в ячейку J21 формулу =J9+J22 и протаскиваем (копируем) её вверх на весь столбец J вспомогательной таблицы: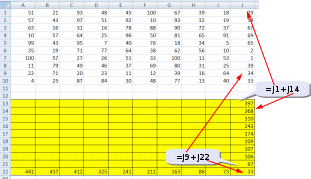
   

8. 
   займёмся центральными ячейками жёлтой таблицы, которые пока не заполнены; пусть Робот находится в ячейке I9; тогда для того, чтобы получить максимальную сумму, ему нужно выбрать лучший из двух путей – пойти в I10 или в J9; из второй таблицы видим, что в первом случае дополнительно к значению I9 он получит сумму 73, а во втором – только 67. поэтому выгоднее первый вариант; в формуле нужно выбрать максимум из значений ячеек I10 и J9, получаем =I9+МАКС(I22;J21); обратите внимание, что оба аргумента функции МАКС находятся в рабочей таблице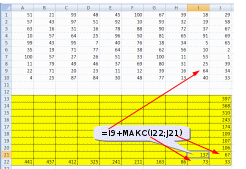
   

9. 
   для всех оставшихся ячеек принцип вычисления максимальной суммы тот же самый: нужно добавить к значению этой ячейки в исходной таблице максимум из накопленных сумм, которые Робот собирает в случае двух возможных шагов; копируем формулу из I21 на весь диапазон A13:I21 (сначала можно растянуть формулу на диапазон-столбец I13:I21, а затем этот диапазон – на нужный диапазон A13:I21)
   

Первый ответ к задаче – это максимальная сумма, накопленная при движении из левого верхнего угла; она записана в левом верхнем углу рабочей таблицы, то есть в ячейке A13 (она выделена зелёным фоном):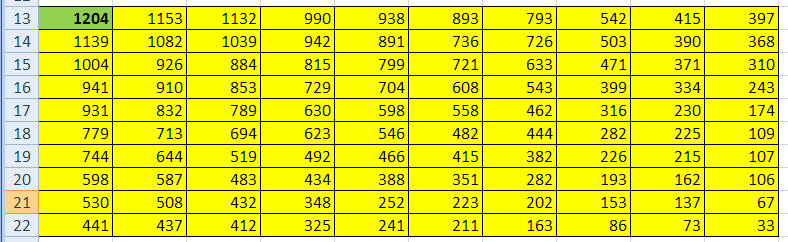

10. 
    чтобы найти наименьшую возможную сумму, нужно в формуле в п. 9 заменить функцию МАКС на МИН: =I9+МИН(I22;J21)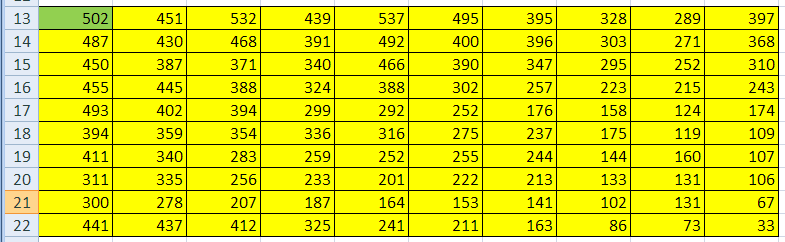
    

11. 
    Ответ: 1204 502
    
12. 
    заметим, что решение никак не зависит от того, что таблица квадратная; этот метод так же хорошо работает и для любых прямоугольных таблиц
    
13. 
    видеоразбор решения этой задачи сделал А. Сидоров (https://www.youtube.com/watch?v=xoKzzj5QX18)
    
14. 
    можно обойтись вообще одной формулой, если добавить к рабочей таблице дополнительно нулевую строку внизу и нулевой столбец справа (Д.Ф. Муфаззалов, М.В. Кузнецова):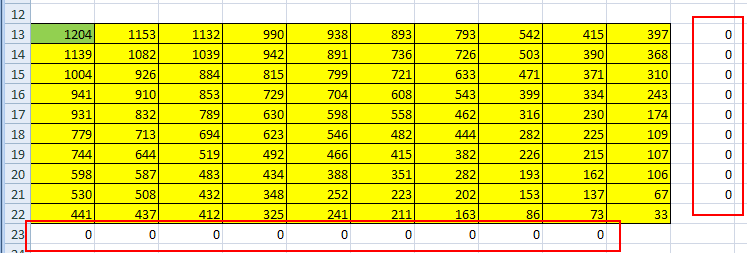
    

15. 
    в этом случае во все ячейки можно скопировать ту формулу, которую мы внесли в ячейку I21
    
16. 
    поскольку функции МАКС и МИН игнорируют пустые ячейки, записывать в дополнительные ячейки нули вообще не нужно!;
    
17. 
    удобнее всего вписать в ячейку J22, соответствующую конечной точке маршрута, аналогичную формулу =J10+МАКС(J23;K22)
    

и затем скопировать её во все остальные ячейки рабочей таблицы

18. 
    (М.В. Кузнецова) если вам удобнее заполнять таблицу слева направо и сверху вниз, можно найти стоимость обратного маршрута (из правой нижней ячейки в левую верхнюю), ведь в данной задаче они одинаковы; для этого освобождаем строку выше и столбец левее рабочей таблицы и вводим в её левый верхний угол формулу =A1+МАКС(A13;B12); эту формулу копируем на всю таблицу, и считываем ответ в правом нижнем углу рабочей таблицы: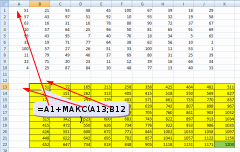
    

Решение (программа):

1. 
   в наборе файлов к этому заданию должен быть файл с расширением .csv (англ. commaseparatedvalues– значения, разделённые запятыми); чаще всего в качестве разделителя используется точка с запятой; если такого файла нет, его можно всегда получить, сохранив электронную таблицу в формате CSV; в данной задаче файл 18-0.csv выглядит так:
   

51;21;93;48;45;100;67;39;18;29

57;43;97;51;92;10;93;32;19;58

63;16;31;16;78;88;90;72;37;67

10;57;64;25;96;50;81;65;91;69

99;43;95;7;40;76;18;34;5;65

35;19;71;77;64;38;62;56;10;2

100;57;27;26;51;33;100;11;53;1

11;79;49;46;37;69;80;31;25;39

22;71;20;23;11;12;39;16;64;34

4;25;87;84;30;48;77;13;40;33

2. 
   напишем программу на языке Python, поскольку на других языках она получится значительно сложнее и использование такого подхода становится, мягко говоря, не очень обоснованно
   
3. 
   сначала читаем данные из файла в матрицу (двухмерный массив) data, попутно определяем размеры матрицы: число строк N и число столбцов M:
   

data = []

for s in open( "18-0.csv" ):

row = list( map( int, s.split(';') ) )

data.append( row )

N = len( data )

M = len( data[0] )

4. 
   строим рабочую матрицу такого же размера, что и исходная; заполняем её нулями:
   

work = [ [0]*M for i in range(N) ]

5. 
   заполняем ячейку в правом нижнем углу (конечная точка маршрута Робота); учитываем, что нумерация строк и столбцов матрицу в Python начинается с нуля, так что эта ячейка имеет индексы N-1, M-1:
   

work[N-1][M-1] = data[N-1][M-1]

6. 
   заполняем последнюю строку (с индексом N-1) справа налево:
   

for col in range(M-2,-1,-1):

work[N-1][col] = data[N-1][col] + work[N-1][col+1]

7. 
   заполняем последний столбец (с индексом M-1) снизу вверх:
   

for row in range(N-2,-1,-1):

work[row][M-1] = data[row][M-1] + work[row+1][M-1]

8. 
   заполняем центральную часть (сверху вниз, справа налево):
   

for row in range(N-2,-1,-1):

for col in range(M-2,-1,-1):

work[row][col] = data[row][col] + \

max(work[row][col+1], work[row+1][col])

в данном случае программа будет искать максимальную сумму; для поиска минимальной суммы нужно заменить функцию max на min

9. 
   остаётся вывести ответ – значение левого верхнего угла рабочей матрицы work, то есть значение ячейки с нулевыми индексами:
   

print( work[0][0] )

10. 
    приведём полную программу:
    

data = []

for s in open( "18-0.csv" ):

row = list( map( int, s.split(';') ) )

data.append( row )

N = len( data )

M = len( data[0] )
work = [ [0]*M for i in range(N) ]

work[N-1][M-1] = data[N-1][M-1]
for col in range(M-2,-1,-1):

work[N-1][col] = data[N-1][col] + work[N-1][col+1]
for row in range(N-2,-1,-1):

work[row][M-1] = data[row][M-1] + work[row+1][M-1]
for row in range(N-2,-1,-1):

for col in range(M-2,-1,-1):

work[row][col] = data[row][col] + max(work[row][col+1], work[row+1][col])
print( work[0][0] )

11. 
    ещё раз обратим внимание на то, что такой способ решения задачи рекомендуется только тем, кто значительно лучше владеет программированием, чем электронными таблицами
    
12. 
    (Муфаззалов Д.Ф., г. Уфа) Программу можно сократить, если использовать одну формулу, содержащую элементы справа и снизу данного элемента, для всех элементов матрицы. Рассмотрим сначала случай поиска минимальной суммы. Так как у элементов на последней строке и в последнем столбце нет элементов снизу и справа соответственно, добавим к матрице один столбец справа и одну строку снизу. Элемент на последней строке в последнем столбце матрицы work должен быть равен такому же элементу матрицы data, поэтому элементы справа и снизу от него должны быть равны нулю. Остальные элементы матрицы work на последней строке и последнем столбце не должны зависеть от элементов снизу и справа соответственно, поэтому там должны быть числа, не влияющие на выбор значения, то есть гораздо большие чем другое число. Поместим туда сумму элементов матрицы.
    

data = []

ma=0

for s in open( "18-0.csv" ):

row = list( map( int, s.split(' ,') ) )

data.append( row )

ma += sum(row)

N = len( data )+1

M = len( data[0] )+1

work = [ [ma]*M for i in range(N) ]

work[N-2][M-1], work[M-1][N-2] = 0, 0

for row in range(N-2,-1,-1):

for col in range(M-2,-1,-1):

work[row][col] = data[row][col] + min(work[row][col+1], work[row+1][col])

print( work[0][0] )

Для случая поиска максимальной суммы все дополнительные элементы сделаем нулевыми:

data = []

ma = 0

for s in open( "18-0.csv" ):

row = list( map( int, s.split(' ,') ) )

data.append( row )

ma += sum(row)

N = len( data )+1

M = len( data[0] )+1

work = [ [0]*M for i in range(N) ]

work[N-2][M-1], work[M-1][N-2] = 0, 0

for row in range(N-2,-1,-1):

for col in range(M-2,-1,-1):

work[row][col] = data[row][col] + max(work[row][col+1], work[row+1][col])

print( work[0][0] )

Решение (программа на С++, В.А. Калинин):

1. 
   полный текст программы:
   

#include

#include

#include

#include

using namespace std;

int main() {

ifstream file_name("18-0.csv");

char delimiter = ';'; //Разделитель

vector<vector<int>> data; //Записываем всю таблицу

string s; //Считываем из фала в строку

while(!file_name.eof())

{

getline(file_name, s);

if (!s.empty()) { //Обязательно проверяем строку на пустоту

stringstream stream(s); // Преобразуем в поток

vector<int> d; // Будем записывать значения,

// которые будут в строке

string num;

while(getline(stream, num, delimiter))

d.push_back(atoi(num.c_str()));

data.push_back(d);

}

}

int N = data.size();

int M = data[0].size();

int calc[N][M] = {0};

calc[N - 1][M - 1] = data[N - 1][M - 1];

for(int i = M - 2; i >= 0; i--)

calc[N - 1][i] = data[N-1][i] + calc[N-1][i+1];

for(int i = N - 2; i >= 0; i--)

calc[i][M - 1] = data[i][M - 1] + calc[i + 1][M - 1];

for(int i = N - 2; i >= 0; i--)

for(int j = M - 2; j >= 0; j--)

calc[i][j] = data[i][j] +

max(calc[i][j + 1], calc[i + 1][j]);

cout << calc[0][0];

return 0;

}
Решение (программа на Java, М. Коротков):

1. 
   полный текст программы:
   

import java.io.IOException;

import java.nio.file.Files;

import java.nio.file.Paths;

import java.util.Arrays;

public class Main {

public static void main(String[] args) throws IOException {

// считываем данные из файла в двумерный массив

Integer[][] data = Files.lines(Paths.get("18-0.csv"))

.map(line -> Arrays.stream(line.split(";"))

.map(Integer::parseInt)

.toArray(Integer[]::new))

.toArray(Integer[][]::new);

final int N = data.length;

final int M = data[0].length;

int[][] calc = new int[N][M];

calc[0][0] = data[0][0];

// заполняем первую строку

for (int j = 1; j < M; j++)

calc[0][j] = data[0][j] + calc[0][j-1];

// заполняем первый столбец

for (int i = 1; i < N; i++)

calc[i][0] = data[i][0] + calc[i-1][0];

// заполняем оставшиеся ячейки

for (int i = 1; i < N; i++)

for (int j = 1; j < M; j++)

// для нахождения мин. суммы Math.max

// заменить на Math.min

calc[i][j] = data[i][j] +

Math.max(calc[i-1][j], calc[i][j-1]);

System.out.println("Ответ: " + calc[N-1][M-1]);

}

}