Длинная линия без потерь. Длинная линия без потерь

• Название: Длинная линия без потерь
• Дата: 01.03.2023
• Размер: 84 Kb.
• Имя файла: Длинная линия без потерь.doc
• Тип: Задача; #962569

Длинная линия без потерь (задача на расчёт линии с распределёнными параметрами)

Текст задачи
«Рассчитайте распределение действующих значений напряжения и тока вдоль длинной линии без потерь (параметры L₀=0,35 мкГн/м, C₀=21 пФ/м). Частота передаваемого гармонического сигнала f=0,7 ГГц. Режим работы линии — R_н=2Z_в. Мгновенное значение тока i₂(t)=25sin(2πft+40^o). Длина линии λ=18 см. Постройте графики U(y), I(y) и определите значение коэффициента бегущей волны».

Дано
L₀=0,35 мкГн/м;
C₀=21 пФ/м;
f=0,7 ГГц;
R_н=2Z_в;
i₂(t)=25sin(2πft+40^o);
λ=18 см. 

Решение

Находим циклическую частоту::


Найдем волновое сопротивление линии, предполагая, что сопротивление провода нулевое, а сопротивление между проводами бесконечно («линия без потерь»).


Находим постоянную распространения:


Тогда коэффициент фазы равен:


Введем условное обозначение m: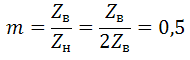


Распределение тока в линии в зависимости от расстояния от конца линии:


Мгновенные значения напряжения:


Распределение напряжения в линии в зависимости от расстояния от конца линии:


График напряжения на линии, как функции от расстояния от конца линии y: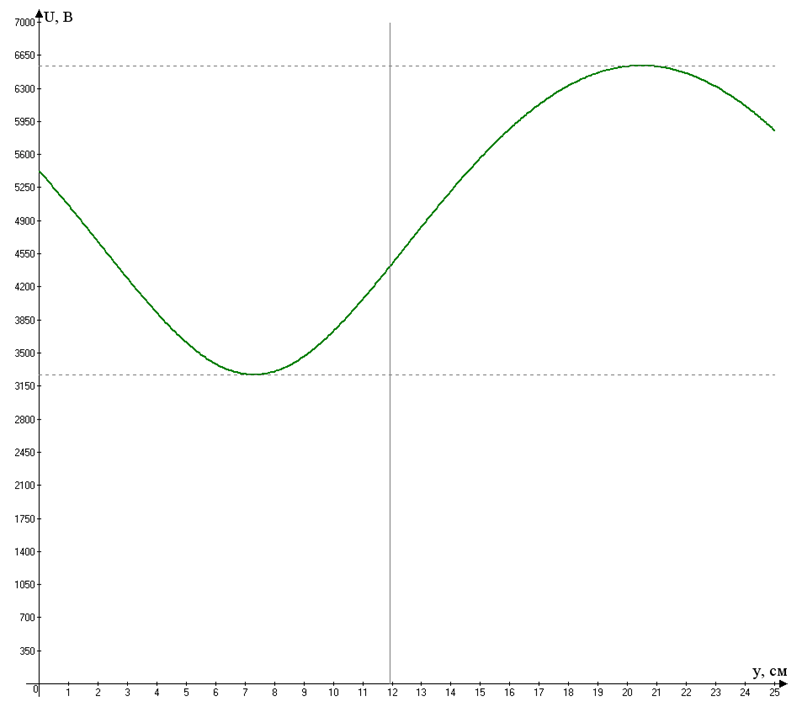


График построен дальше начала линии (обозначено вертикальной линией) для определения минимума и максимума напряжения смешанной волны.
Коэффициент бегущей волны – отношение минимума напряжения смешанной волны к её максимуму – определяем по графику.
K_б.в.=3270/6540=0,5;

График тока на линии, как функции от расстояния от конца линии y: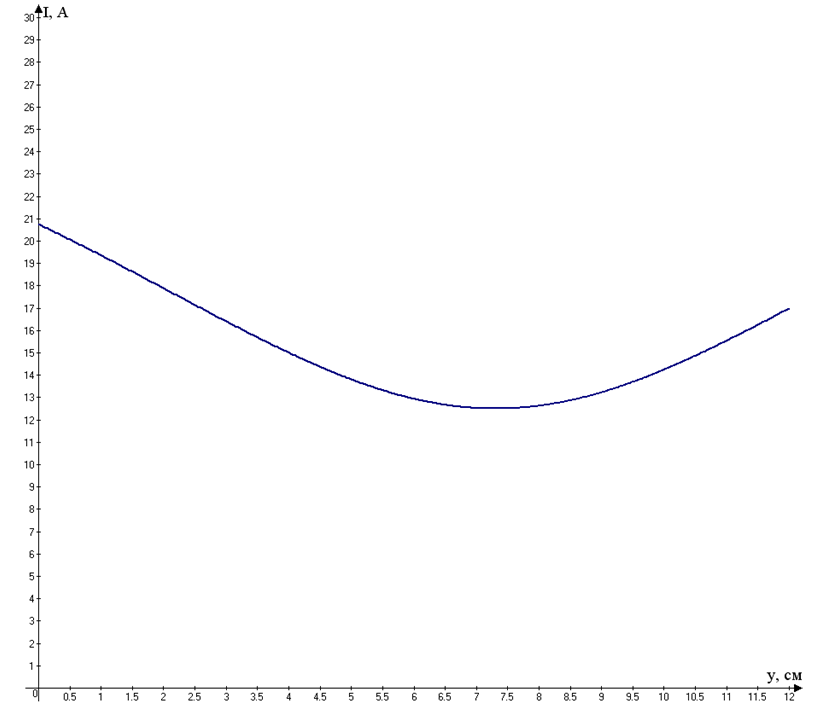