Движения в пространстве. Движения в пространстве Перечень вопросов, рассматриваемых в теме понятие движение
 Скачать 118.76 Kb.
|
|
Движения в пространстве Перечень вопросов, рассматриваемых в теме: понятие «движение» в пространстве; свойства движений в пространстве; виды движений в пространстве; отличия движений в пространстве от движений на плоскости. 1. Определение движения в пространстве Допустим, что каждой точке А пространства поставлена в соответствие точка А1 пространства. При этом каждая точка А1 поставлена в соответствие какой-то точке А. Тогда говорят, что задано отображение пространства на себя. При этом точка А перешла в точку А1. А1 - образ точки А. Преобразованием пространства называется взаимно-однозначное отображение пространства на себя. Два преобразования называются равными, если образы любой точки при этих преобразованиях совпадают. Точка А называется неподвижной точкой при некотором преобразовании f, если при этом преобразовании она отображается на себя. Фигура F называется неподвижной фигурой при некотором преобразовании f, если при этом преобразовании она отображается на себя. Преобразование пространства, которое каждую точку отображает на себя, называется тождественным преобразованием. Оно обычно обозначается Е. При тождественном преобразовании все точки и все фигуры пространства являются неподвижными. Для любых двух преобразований можно рассмотреть третье, которое получается последовательным применением этих преобразований. Например, если преобразование f отображает точку М на точку М', а преобразование g отображает точку М' на точку M'', то преобразование f°g отображает точку М на точку M'': f°g(М)=g(f(M))=M''. f°g - композиция преобразований f и g. Под движением пространства понимается отображение пространства на себя, при котором любые две точки A и B переходят (отображаются) в некие точки A1 и B1 так, что |AB|=|A1B1|. Иными словами, движение пространства — это отображение пространства на себя, сохраняющее расстояния между точками. Так же, как и для движения на плоскости, можно доказать, что при движении в пространстве - прямые переходят в прямые, - полупрямые — в полупрямые, - отрезки — в отрезки, - сохраняются углы между прямыми. Новое свойство движения в пространстве: движение переводит плоскости в плоскости. В пространстве, так же как и на плоскости, две фигуры называются равными, если они совмещаются движением. Можно доказать, что композиция двух движений пространства есть движение. 2. Виды движений. Центральная симметрия. Центральная симметрия в пространстве задается и определяется так же, как и на плоскости Определение: Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно точки O, называется центральной симметрией пространства относительно точки O. При этом точка O отображается на себя и называется центром симметрии. 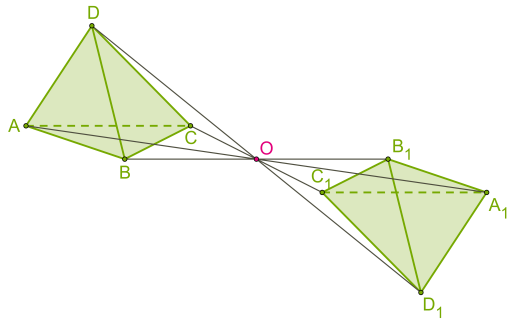 Рисунок 1 – Центральная симметрия На рисунке точка О – центр симметрии, АО=А1О, ВО=В1О, СО=С1О, DО=D1О (по определению точки, симметричной данной). Центральная симметрия имеет только одну неподвижную точку – центр симметрии. Сформулируем некоторые свойства центральной симметрии: 1) Прямая, проходящая через центр симметрии, отображается на себя. 2) Прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую. 3) Плоскость, проходящая через центр симметрии, отображается на себя (то есть является неподвижной плоскостью этой центральной симметрии). 4) Плоскость, не проходящая через центр симметрии, отображается на параллельную ей плоскость. 3. Осевая симметрия (симметрия относительно прямой): Определение:_Преобразование_пространства,_при_котором_каждая_точка_пространства_отображается_на_точку,_симметричную_ей_относительно_прямой_m,_называется_осевой_симметрией'>Определение: Точка M' пространства, не лежащая на прямой m, называется симметричной точке М относительно прямой m, если отрезок ММ' перпендикулярен этой прямой и делится ею пополам. Определение: Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно прямой m, называется осевой симметрией пространства относительно прямой m. Прямая m отображается на себя и называется осью симметрии. 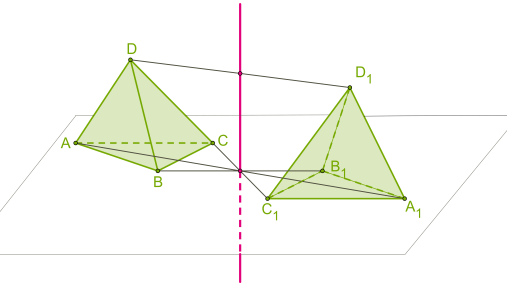 Рисунок 2 – Осевая симметрия Неподвижные точки осевой симметрии - любая точка прямой m. Неподвижные прямые осевой симметрии: 1) сама прямая m 2) любая прямая, перпендикулярная прямой m Неподвижные плоскости осевой симметрии: 1) любая плоскость, проходящая через прямую m 2) любая плоскость, перпендикулярная прямой m. Зеркальная симметрия (симметрия относительно плоскости): Определение: Точка M' пространства, не лежащая на плоскости α, называется симметричной точке М относительно плоскости α, если отрезок ММ' перпендикулярен этой плоскости и делится ею пополам. Определение: Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно плоскости α, называется зеркальной симметрией пространства относительно плоскости α. Плоскость αотображается на себя и называется плоскостью симметрии. 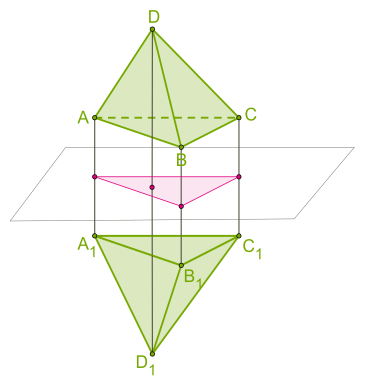 Рисунок 3 – Зеркальная симметрия Неподвижные точки зеркальной симметрии - любая точка плоскости α. Неподвижные прямые зеркальной симметрии: 1) любая прямая плоскости α 2) любая прямая, перпендикулярная плоскости α Неподвижные плоскости зеркальной симметрии: 1) сама плоскость α 2) любая плоскость, перпендикулярная плоскости α. Параллельный перенос (точки переносятся на данный вектор): 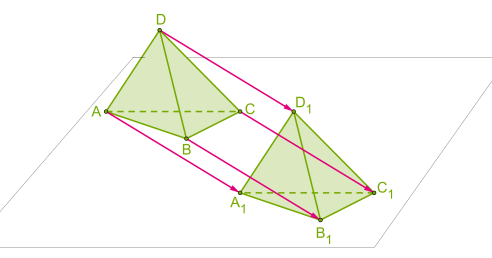 Рисунок 4 – параллельный перенос Определение Пусть дан вектор  .Преобразование пространства, при котором каждая точка пространства M, отображается на такую точку M', что выполняется равенство  , называется параллельным переносом на вектор  .Перенос на нулевой вектор  является тождественным преобразованием.Параллельный перенос отображает прямую на параллельную ей прямую либо на себя; плоскость на параллельную ей плоскость либо на себя. Неподвижных точек параллельный перенос на ненулевой вектор не имеет. Неподвижными прямыми при параллельном переносе на вектор являются прямые, параллельные этому вектору.Неподвижными плоскостями при параллельном переносе на вектор являются плоскости, параллельные этому вектору.Поворот на данный угол вокруг данной оси: Определение: Поворотом пространства на угол φ вокруг прямой n называется такое преобразование пространства, при котором любая точка прямой остается неподвижной и в любой плоскости, перпендикулярной прямой n, осуществляется поворот этой плоскости на угол φ вокруг точки ее пересечения с прямой n. 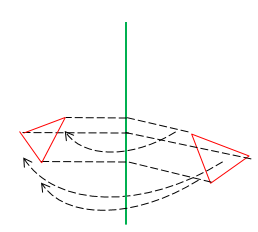 Рисунок 5 – Поворот вокруг прямой Неподвижными точками являются любая точка оси вращения. Неподвижной прямой является ось поворота. Неподвижной плоскостью является любая плоскость, перпендикулярная оси поворота. Поворот вокруг оси на угол 1800 является осевой симметрией. |