Шпаргалки Векторная алгебра. Аналитическая геометрия. Детские подарки. Эллипс. Определение Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами
 Скачать 162.93 Kb. Скачать 162.93 Kb.
|
|
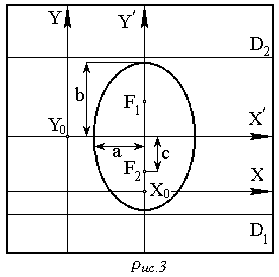
Эллипс.  Определение: Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами Если оси координат расположены по отношению к эллипсу так, как показано на рисунке 1, а фокусы эллипса находятся на оси  Здесь Форма эллипса (мера его "сжатия") характеризуется его эксцентриситетом.  (так как (так как Прямые:  и и перпендикулярные главной оси и проходящие на расстоянии перпендикулярные главной оси и проходящие на расстоянии Расположение эллипса и его параметры
Эксцентриситет 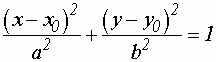
Уравнения директрис
Гипербола 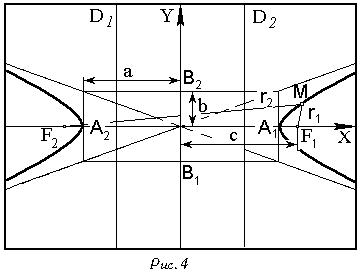 Определение: гиперболой называется множество точек плоскости, абсолютная величина разности которых до двух данных точек, называемых фокусами, есть величина постоянная (ее обозначают через Если поместить фокусы гиперболы в точках 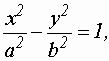 где где Точки: Гипербола имеет две асимптоты, уравнения которых  . .Отношение  называется эксцентриситетом гиперболы. называется эксцентриситетом гиперболы.Уравнение  также является уравнением гиперболы, но действительной осью этой гиперболы служит отрезок оси также является уравнением гиперболы, но действительной осью этой гиперболы служит отрезок оси Две гиперболы  и и  имеют одни и те же полуоси и одни и те же асимптоты, но действительная ось одной служит мнимой осью другой, и наоборот. Такие две гиперболы называются сопряженными. имеют одни и те же полуоси и одни и те же асимптоты, но действительная ось одной служит мнимой осью другой, и наоборот. Такие две гиперболы называются сопряженными.Прямые  и и 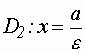 , перпендикулярные действительной оси и проходящие на расстоянии , перпендикулярные действительной оси и проходящие на расстоянии Расположение гиперболы
1)  ; ;  -эксцентриситет. -эксцентриситет.2)  ; ;  - эксцентриситет. - эксцентриситет.Уравнение директрис гиперболы 1)  ; ;  . .2)  ; ; 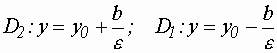 . .Парабола  Определение: Параболой называется множество точек плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Если директрисой параболы является прямая: 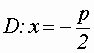 , а фокусом - точка , а фокусом - точка , то уравнение параболы имеет вид: , то уравнение параболы имеет вид: Положение параболы и ее параметры 1)
2)
Уравнение директрисы параболы  ; ;  . . ; ;  . . |





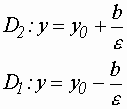
 ;
; ;
;

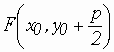 :
:
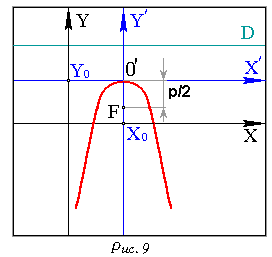
 :
:
