создание граф. Гипербола и её каноническое уравнение
 Скачать 204.95 Kb.
|
|
Гипербола и её каноническое уравнение Общая структура изложения материала будет напоминать предыдущий параграф. Начнём с общего понятия гиперболы и задачи на её построение. Каноническое уравнение гиперболы имеет вид  , где  – положительные действительные числа. Обратите внимание, что в отличие от эллипса, здесь не накладывается условие  , то есть, значение «а» может быть и меньше значения «бэ».Надо сказать, довольно неожиданно… уравнение «школьной» гиперболы  и близко не напоминает каноническую запись. Но эта загадка нас ещё подождёт, а пока почешем затылок и вспомним, какими характерными особенностями обладает рассматриваемая кривая? Раскинем на экране своего воображения график функции ….У гиперболы две симметричные ветви. У гиперболы две асимптоты. Неплохой прогресс! Данными свойствами обладает любая гипербола, и сейчас мы с неподдельным восхищением заглянем в декольте этой линии: Пример 4 Построить гиперболу, заданную уравнением  Решение: на первом шаге приведём данное уравнение к каноническому виду 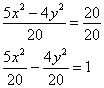. Пожалуйста, запомните типовой порядок действий. Справа необходимо получить «единицу», поэтому обе части исходного уравнения делим на 20: Здесь можно сократить обе дроби, но оптимальнее сделать каждую из них трёхэтажной: 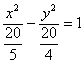 И только после этого провести сокращение:  Выделяем квадраты в знаменателях:  Готово. Почему преобразования лучше проводить именно так? Ведь дроби левой части 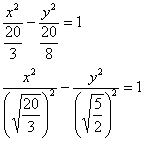 можно сразу сократить и получить . Дело в том, что в рассматриваемом примере немного повезло: число 20 делится и на 4 и на 5. В общем случае такой номер не проходит. Рассмотрим, например, уравнение  . Здесь с делимостью всё печальнее и без трёхэтажных дробей уже не обойтись: Итак, воспользуемся плодом наших трудов – каноническим уравнением :Как построить гиперболу? Существует два подхода к построению гиперболы – геометрический и алгебраический. С практической точки зрения вычерчивание с помощью циркуля... я бы даже сказал утопично, поэтому гораздо выгоднее вновь привлечь на помощь нехитрые расчёты. Целесообразно придерживаться следующего алгоритма, сначала готовый чертёж, потом комментарии: 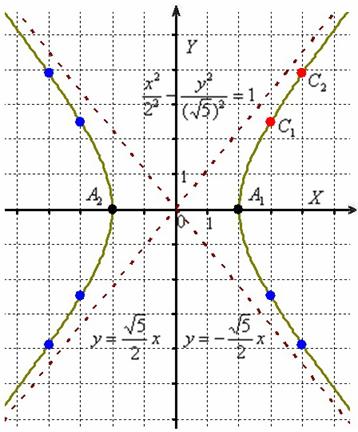 1) Прежде всего, находим асимптоты. Если гипербола задана каноническим уравнением , то её асимптотами являются прямые  . В нашем случае:  . Данный пункт обязателен! Это принципиальная особенность чертежа, и будет грубой ошибкой, если ветви гиперболы «вылезут» за свои асимптоты.2) Теперь находим две вершины гиперболы, которые расположены на оси абсцисс в точках  . Выводится элементарно: если  , то каноническое уравнение превращается в  , откуда и следует, что  . Рассматриваемая гипербола имеет вершины  3) Ищем дополнительные точки. Обычно хватает двух-трёх. В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для 1-й координатной четверти. Методика точно такая же, как и при построении эллипса. Из канонического уравнения 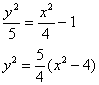на черновике выражаем: Уравнение распадается на две функции:  – определяет верхние дуги гиперболы (то, что нам надо); – определяет нижние дуги гиперболы.Напрашивается нахождение точек с абсциссами 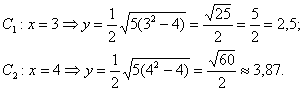 : 4) Изобразим на чертеже асимптоты , вершины , дополнительные  и симметричные им точки в других координатных четвертях. Аккуратно соединим соответствующие точки у каждой ветви гиперболы:Техническая трудность может возникнуть с иррациональным угловым коэффициентом  , но это вполне преодолимая проблема.Отрезок  называют действительной осью гиперболы,его длину  – расстоянием между вершинами; число  называют действительной полуосью гиперболы; число  – мнимой полуосью.В нашем примере:  , и, очевидно, если данную гиперболу повернуть вокруг центра симметрии и/или переместить, то эти значения не изменятся.Определение гиперболы. Фокусы и эксцентриситет У гиперболы, точно так же, как и у эллипса, есть две особенные точки  , которые называются фокусами. Не говорил, но на всякий случай, вдруг кто неверно понимает: центр симметрии и точки фокуса, разумеется, не принадлежат кривым.Общая концепция определения тоже похожа: Гиперболой называют множество всех точек плоскости, абсолютное значение разности расстояний до каждой из которых от двух данных точек – есть величина постоянная, численно равная расстоянию между вершинами этой гиперболы:  . При этом расстояние между фокусами превосходит длину действительной оси:  .Если гипербола задана каноническим уравнением , то расстояние от центра симметрии до каждого из фокусов рассчитывается по формуле:  . И, соответственно, фокусы имеют координаты  .Для исследуемой гиперболы 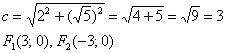: Разбираемся в определении. Обозначим через 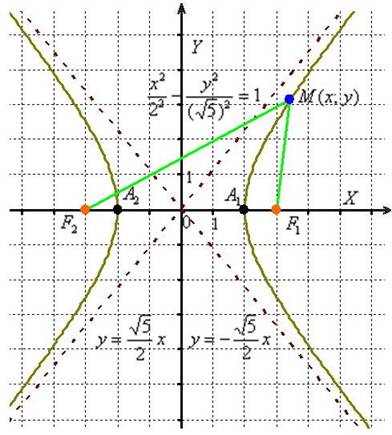 расстояния от фокусов до произвольной точки  гиперболы: Сначала мысленно передвигайте синюю точку по правой ветви гиперболы – где бы мы ни находились, модуль (абсолютное значение) разности между длинами отрезков  будет одним и тем же: Если точку «перекинуть» на левую ветвь, и перемещать её там, то данное значение останется неизменным.Знак модуля нужен по той причине, что разность длин  может быть как положительной, так и отрицательной. Кстати, для любой точки правой ветви  (поскольку отрезок  короче отрезка  ). Для любой точки левой ветви ситуация ровно противоположная и  .Более того, ввиду очевидного свойства модуля  безразлично, что из чего вычитать.Удостоверимся, что в нашем примере модуль данной разности действительно равен расстоянию между вершинами. Мысленно поместите точку в правую вершину гиперболы  . Тогда:  , что и требовалось проверить.Эксцентриситетом гиперболы называют отношение  .Так как расстояние от центра до фокуса больше расстояния от центра до вершины:  , то эксцентриситет гиперболы всегда больше «единицы»:  .Для данного примера:  .По аналогии с эллипсом, зафиксировав значение  , желающие могут провести самостоятельный анализ и проверку следующих фактов:При увеличении эксцентриситета ветви гиперболы «распрямляются» к оси  .В предельном случае  они стремятся занять положение двух прямых, проходящих через точки  параллельно оси ординат.Если же значение эксцентриситета приближается к единице, то ветви гиперболы «сплющиваются» к оси  .Равносторонняя гипербола На практике часто встречается гипербола с равными полуосями. Если  , то каноническое уравнение заметно упрощается: А вместе с ним упрощаются и уравнения асимптот: 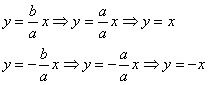 Прямые  пересекаются под прямым углом и «справедливо» делят координатную плоскость на 4 одинаковые части, в двух из которых находятся ветви кривой. Образно говоря, равносторонняя гипербола «идеально сложена», то есть и не растянута и не сплющена.Так как , то  , следовательно, эксцентриситет любой равносторонней гиперболы равен:  .Предлагаю закрепить теорию и практические навыки миниатюрной задачей: Пример 5 Построить гиперболу  и найти её фокусы.Это пример для самостоятельного решения. Кто пропустит, тот пропустит многое ;-) Решение и чертёж в конце урока. Начнём тревожить беззаботное существование нашей кривой: Поворот вокруг центра и параллельный перенос гиперболы Вернёмся к демонстрационной гиперболе . Что произойдёт, если в полученном уравнении поменять значения полуосей:  ? Для эллипса данный трюк означал поворот на 90 градусов. Но здесь всё иначе! Уравнение определяет совершенно другую гиперболу. Ну, хотя бы обратите внимание на иные вершины:  .Теперь рассмотрим уравнение  , которое очевидно тоже задаёт гиперболу. Однако к исходному уравнению оно также не имеет никакого отношения! Это предыдущая гипербола, повёрнутая на 90 градусов, с вершинами  на оси ординат.И, наконец, оставшийся случай  задаёт нашу гиперболу , повернутую на 90 градусов. Как быть, если в практической задаче встретилась такая неканоническая запись?Если требуется только построить кривую, то, наверное, лучше построить её в нестандартном виде. Это довольно просто. Уравнения асимптот гиперболы обладают обратными угловыми коэффициентами: Поскольку оси «поменялись ролями», то вершины будут расположены на оси ординат в точках 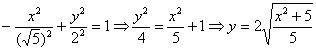 . Выразим верхнюю ветвь гиперболы: И найдём несколько дополнительных точек: 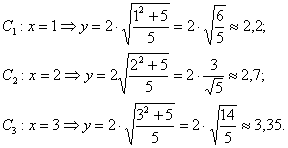 Выполним чертёж: 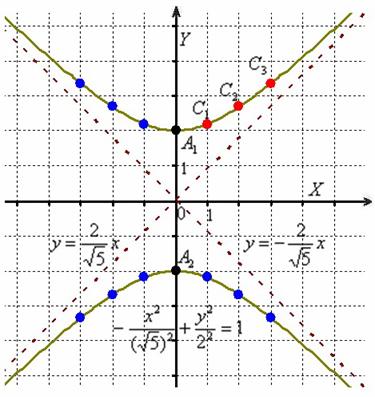 Помимо геометрии, похожие графики требуется строить в некоторых задачах математического анализа. Однако по возможности всё-таки лучше осуществить поворот на 90 градусов и переписать уравнение в канонической форме. Для этого следует поменять местами значения полуосей и переставить «минус» к переменной «игрек»: . И далее работать уже с каноническим уравнением. ! Примечание: строгий теоретический подход предполагает поворот координатных осей, а не самой линии. При необходимости оформляйте решение по аналогии с соответствующим примечанием предыдущего урока. Параллельный перенос. Уравнение  задаёт гиперболу с действительной полуосью «а», мнимой полуосью «бэ» и центром в точке  .Так, например, гипербола 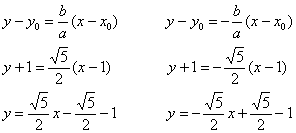 имеет центр симметрии в точке  . Асимптоты, само собой, переместились вместе с гиперболой, их уравнения отыскиваются по формулам: Полуоси 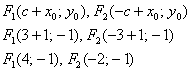 и расстояние от фокусов до центра симметрии  остались прежними, а вот координаты фокусов изменились с учётом параллельного переноса: Параллельный перенос гиперболы доставил заметно больше хлопот, чем параллельный перенос эллипса, смотрим на картинку: 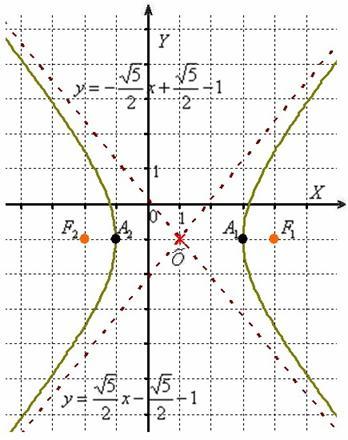 После таких трудов, уравнение трогать бессмысленно, но если таки просят, то придётся…. В нестрогом варианте: «Приведём уравнение гиперболы к каноническому виду путём параллельного переноса в начало координат:  ».Или в строгом – с параллельным переносом системы координат началом в точку (см. шаблон у эллипса). На практике часто встречается комбинация поворота на произвольный угол и параллельного переноса гиперболы. Данная ситуация рассматривается на уроке Приведение уравнения линии 2-го порядка к каноническому виду. |