Размещение прямой и плоскости в пространстве. Признак параллельн. Ход урока ii. Проверка домашнего задания
 Скачать 24.19 Kb.
|
|
Размещение прямой и плоскости в пространстве. Признак параллельности прямой и плоскости Цель урока: формирование знаний учащихся о взаимное размещение прямой и плоскости в пространстве. Изучения признака параллельности прямой и плоскости. Ход урока II. Проверка домашнего задания Собрать тетради в конце урока для проверки их ведения и выполнения домашнего задания. III. Обобщение и систематизация знаний учащихся Взаимное размещение прямой и плоскости в пространстве Вопросы к классу. 1) Вспомните и сформулируйте теорему о принадлежности прямой плоскости, две точки которой принадлежат плоскости. 2) Как могут располагаться прямая и плоскость в пространстве? При обсуждении этого вопроса уместно воспользоваться схемой «Взаимное расположение прямой и плоскости» из урока № 3, с. 21. IV. Восприятие и осознание нового материала Понятие прямой, параллельной плоскости, признак параллельности прямой и плоскости Прямая и плоскость называются параллельными, если они не имеют общих точек. Параллельность прямой а и плоскости α обозначается так: а || a. Наглядное представление о прямой, параллельной плоскости, дают линии пересечения стены и потолка — эти линии параллельны плоскости пола. Отрезок называется параллельным плоскости, если он является частью прямой, параллельной плоскости. Сформулируем и докажем признак параллельности прямой и плоскости. Теорема. Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости. Д 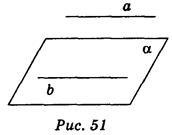 оказательство признака записывается на доске и в тетрадях.Дано: а || b; b  α (рис. 51). Доказать: а || a. Выполнение упражнений 1. Дано изображение куба АВСD1А1B1С1D1. Докажите, что: а) прямая АВ параллельна плоскости DСС1; б) прямая АВ параллельна плоскости DСВ1. 2. В треугольной пирамиде SАВС точки М и N — середины ребер SА и SВ соответствии. Докажите, что МN || (АВС). 3. Даны плоскость a и вне ее точку А. Провести через точку А прямую, параллельную данной плоскости a. Решения А 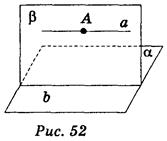 нализ. По условию А и a (рис. 52). Чтобы прямая а, проходящая через точку А, была параллельна плоскости a, достаточно, чтобы она была параллельна прямой b, принадлежащей плоскости a . Отсюда вытекает план решения:1) в плоскости a проводим произвольную прямую b; 2) через прямую b и точку А проводим плоскость b; 3) через точку А проводим прямую а: а || b. Доказательство. Согласно признаку параллельности прямой и плоскости имеем: а || a. Исследования. Прямая b проведенная в плоскости a произвольно, таких прямых бесконечное множество, следовательно, задача имеет бесконечное множество решений. 4. Дано прямую а и точку А, которая не лежит на ней. Провести плоскость, которая проходит через точку А и параллельная прямой а. 5. Даны параллельные прямые а и b. Провести через прямую а плоскость, которая параллельна прямой b. 6. Задача № 15 из учебника (с. 19). 7. Даны скрещивающиеся прямые а и b и точку С, которая не лежит на них. Провести через точку С плоскость, параллельную прямым а и b. V. Домашнее задание § 2, п. 9; контрольные вопросы № 5, 6; задачи .№ 14, 16 (с. 19). VI. Подведение итога урока Вопросы к классу 1) Как могут располагаться прямая и плоскость в пространстве? 2) Сформулируйте признак параллельности прямой и плоскости. |