мом 5 вопрос. I. При первом подходе можно выделить три основных этапа введения понятия мотивационный, введение понятия, первичное закрепление. Мотивационный этап
 Скачать 30.46 Kb. Скачать 30.46 Kb.
|
|
Индивидуальное задание к 1 лабораторной работе Вопрос 5. Различные подходы к введению понятия «Иррациональное число» в школьном курсе. Существует три подхода к введению понятия «иррациональное число». I. При первом подходе можно выделить три основных этапа введения понятия: мотивационный, введение понятия, первичное закрепление. 1. Мотивационный этап. На этом этапе можно предложить решить следующую задачу: «Найти сторону квадрата, площадь которого равна 2». Алгебраической моделью ситуации является уравнение  . Решением этого уравнения (с учетом того, что длина выражается положительным числом) является арифметический квадратный корень из 2. Это число. Встает вопрос: «Какому числовому множеству принадлежит это число?» . Решением этого уравнения (с учетом того, что длина выражается положительным числом) является арифметический квадратный корень из 2. Это число. Встает вопрос: «Какому числовому множеству принадлежит это число?»2. Этап введения понятия. Проиллюстрировать этот этап можно, выполнив лабораторную работу. Примеры. 1) Является ли 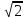 целым числом? целым числом?Ответ. Рассмотрим квадраты последовательных натуральных чисел: 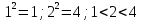 Вывод. Среди целых чисел значения 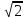 нет. нет.2) Является ли 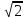 рациональным числом? рациональным числом?Ответ. Рассмотрим приближенные значения 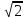 с точностью до 0,01; 0,001 и т.д. с точностью до 0,01; 0,001 и т.д.1,12 = 1,21 1,22 = 1,44 1,32 = 1,69 1,42 = 1,96 1,52 = 2,25 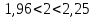 Тогда  . .Выполняя аналогичную работу на отрезке  , получим: , получим: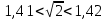 . .Увеличивая точность приближения, можно показать: 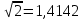 . Уже на этом этапе можно увидеть, что . Уже на этом этапе можно увидеть, что 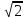 – бесконечная непериодическая дробь. – бесконечная непериодическая дробь.С использованием микрокалькулятора получим: 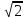 = 1,4142135623…. = 1,4142135623….Вывод (предположение) на этом этапе. 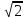 – не рациональное число. – не рациональное число.3) Приведите строгое математическое доказательство предположения, сформулированного на предыдущем этапе. Утверждение. Не существует рационального числа, квадрат которого равен двум. Далее приводится доказательство. (Перед доказательством должна быть проведена подготовительная работа). 4) Существует ли число 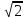 ? ?Ответ. Решим исходное уравнение графически. 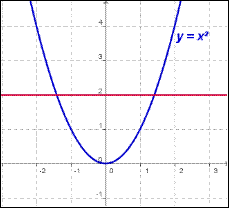 Как видно из рисунка, существует положительное значение абсциссы точки пересечения графиков. Значит, существует число 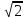 . А это, в свою очередь, требует расширения числового множества. . А это, в свою очередь, требует расширения числового множества.5) Дайте определение иррационального числа. Ответ. Числа, представляемые бесконечными десятичными непериодическими дробями, называются иррациональными. Далее приводятся примеры иррациональных чисел: 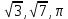 и т.д. и т.д.Введение понятия «иррациональное число» завершается расширением множества рациональных чисел до множества действительных чисел, структуру которого можно изобразить с помощью кругов Эйлера (швейцарский математик 1707-1773). 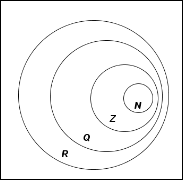 3. Этап первичного закрепления. На этом этапе целесообразно решать задачи на установление взаимосвязи известных числовых множеств, сравнение чисел, изображение чисел точками координатной прямой. II. При втором подходе к ведению понятия «иррациональное число» («Алгебра–8» под ред. С.А. Теляковского) можно предложить ученикам следующие задания. Примеры. 1) Найдите длину отрезка OB при выбранной единице измерения OE.  Эта задача иллюстрирует, что процесс измерения может быть бесконечным, а отрезки несоизмеримыми. 2) Вычислите длины отрезка, если он составляет  единичного отрезка. единичного отрезка.Ответ: 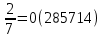 . .3) Приведите геометрическое доказательство того, что отношение площади квадрата, построенного на диагонали данного квадрата, к площади данного равно 2. Ответ. Длина диагонали квадрата равна числу, квадрат которого равен 2; при измерении длины диагонали (при условии, что единица измерения – длина стороны данного квадрата) получается бесконечная непериодическая десятичная дробь. 4) Приведите строгое доказательство, что не существует рационального числа, квадрат которого равен двум. 5) Дайте определение иррационального числа. 6) Постройте множество действительных чисел. III. При третьем подходе к введению понятия (Ш.А. Алимов и др. «Алгебра–8») можно привести формулировку определения и проиллюстрировать его примерами. Бесконечные десятичные непериодические дроби называют иррациональными числами. Рациональные и иррациональные числа образуют множество действительных чисел. Например,  – рациональное число, а – рациональное число, а  – иррациональное число. – иррациональное число.Задача 1. Вычислить на МК приближенное значение  с точностью до 0,001. с точностью до 0,001. Ответ: 3,742 |
