ИНДИВИДУАЛЬНЫЕ КАРТОЧКИ
ПО АЛГЕБРЕ 7 КЛАСС
Романова Е.Г., учитель математики МБОУ СОШ №14 г.Ковров
Карточки охватывают основные вопросы курса. Каждая карточка составлена по одному конкретному вопросу и составлена из трех частей:
1) алгоритма (правила);
2) образца применения алгоритма;
3) заданий.
Карточка № 1. Нахождение значений буквенных выражений
Правило
|
Образец
|
Задание
|
При нахождении значений буквенных выражений нужно поступать так:
1)подставить вместо переменной ее значение;
2)вычислить значение полученного числового
выражения
|
Найти значение выражения:
3 – 5х при х = -3; 0; 2.
Решение.
Если х = -3, то 3 – 5х = 3 – 5 ∙(-3) = 3 + 15 = 18
Если х = 0, то 3 – 5х = 3 – 5 ∙ 0 = 3 – 0 = 3
Если х = 2, то 3 – 5х = 3 – 5 ∙ 2 = 3 – 10 = - 7
|
Найти значение выражения:
1) х + 3,2
при х = -6,8; -3,2; 7,8
2) – 5х
При х = - 2,6; 0; 4
3) 12х – 7
При х = -1; 0; 0,5
4) 3 -1,5х
При х = - 2; 0; 4
|
Карточка № 2. Решение линейного уравнения с одной переменной
Правило
|
Образец
|
Задание
|
При решении уравнения используются следующие свойства:
1)если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то
получится уравнение, равносильное данному;
2)если обе части уравнения умножить или разделить на
одно и то же отличное от нуля
число, то получится уравнение, равносильное данному.
|
Решите уравнение:
1) 4 - х = 1 + 6х.
Решение. Перенесем слагаемые с неиз-
вестным влево, а слагаемые без неиз-
вестных – вправо, меняя их знаки:
- х – 6х = 1 - 4 ,
Приведем подобные:
- 7х = -3,
х = -3 ׃(- 7),
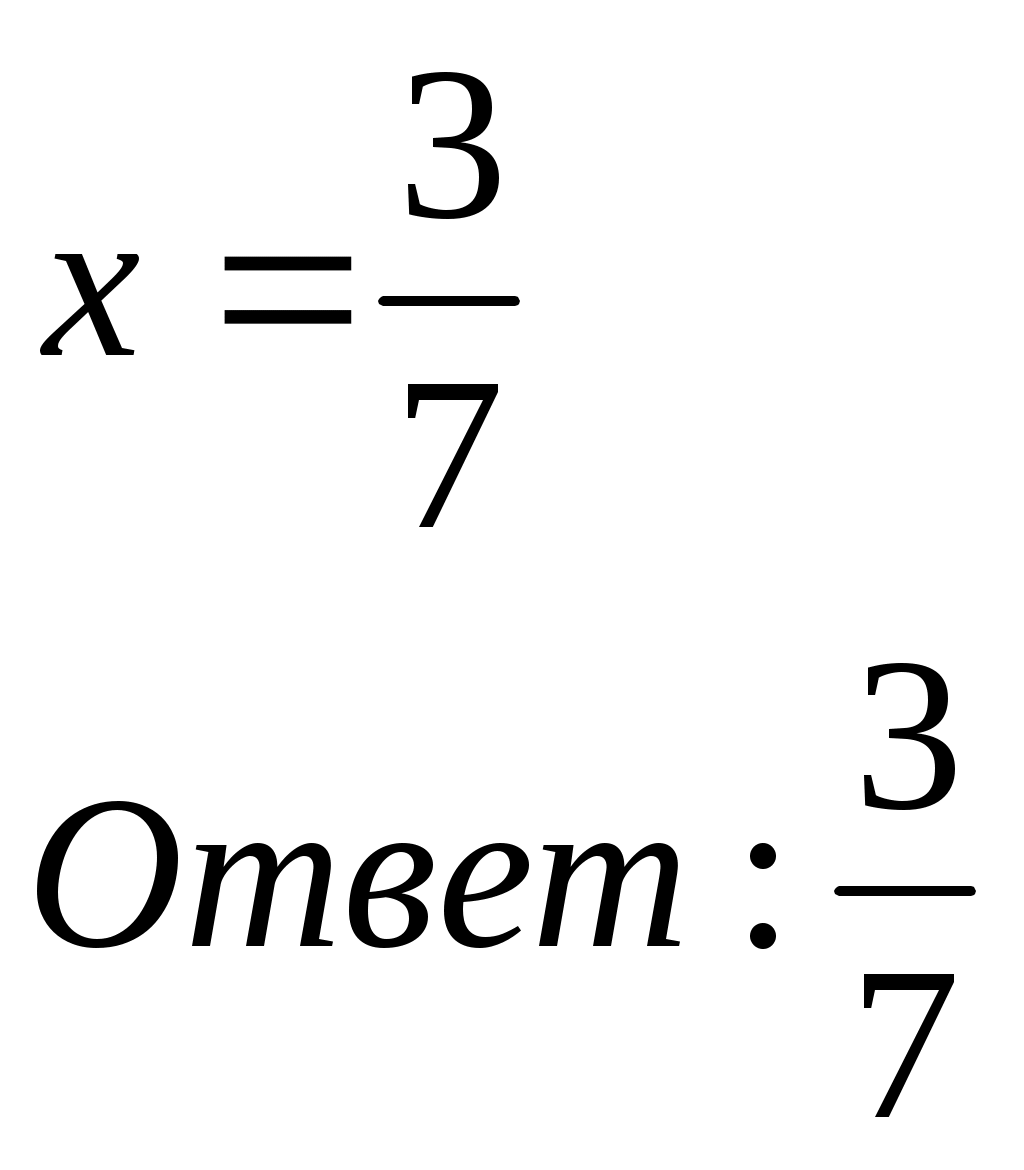
2) -3х = 15.
Решение.
х = 15 ׃(- 3),
х = -5
Ответ: -5
|
Решите уравнение:
1)2х = -14;
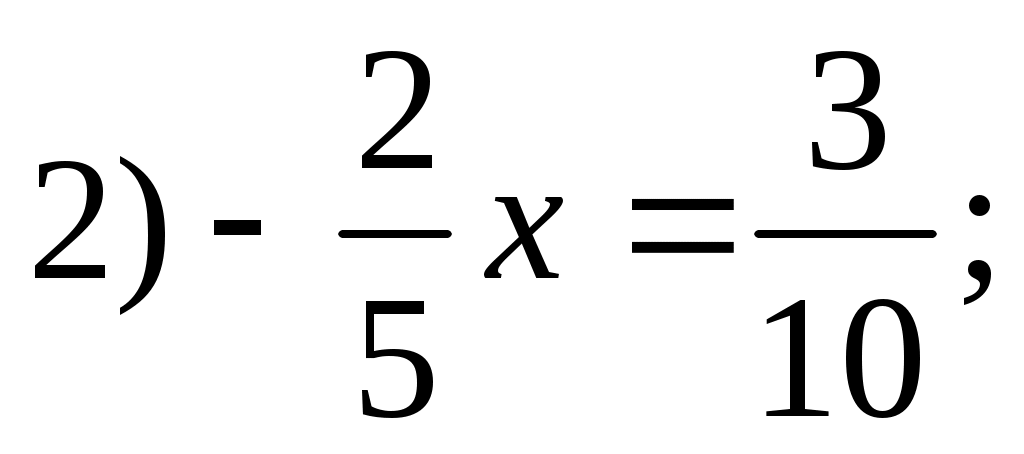
3)4у + 15 = 6у + 17;
4)13 – (5х + 11) = 6х;
5)5(х – 1,2) = 2 + 3х
|
Карточка № 3. Функции и их графики
Правило
|
Образец
|
Задание
|
1)для построения графика
линейной функции y=kx+b
достаточно двух точек графика, причем одна из них с координатами (0;b), и провести через них прямую.
|
Постройте график функции:
1) у = -х +4; 2) у = 3; 3) у = - 2х
Решение.
1) у = - х + 4 – линейная функция
Графиком является прямая.
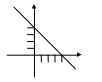
|
Постройте график функции:
а) у = х – 2
б) у = - 3х – 3
|
2)при построении графика
линейной функции y=b
нужно провести прямую
через точку (0;b), параллельную оси Ох.
|
2)y = 3 – линейная функция
Графиком является прямая, проходящая через точку (0;3) и параллельная оси ох.
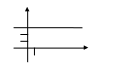
|
Постройте график функции:
а) у = 5
б) у = - 4
|
3) для построения графика
прямой пропорциональности
y=kx достаточно отметить
какую-либо точку графика,
отличную от начала координат,
и провести через эту точку и
начало координат прямую.
|
3)у=-2х – прямая пропорциональность
Графиком является прямая, проходящая через начало координат.
Если х = 1, то у = -2∙1 = -2
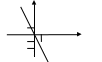
|
Постройте график функции:
а) у = 3х
б) у = - 0,5х
|
Карточка № 4. Степень и её свойства
Правила
|
Образец
|
Задание
|
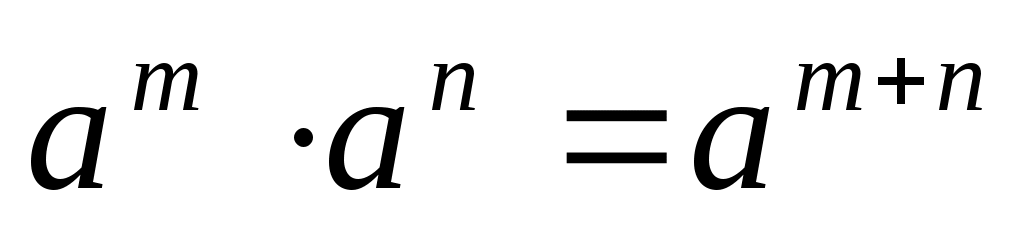



|
Упростите выражение:
а) 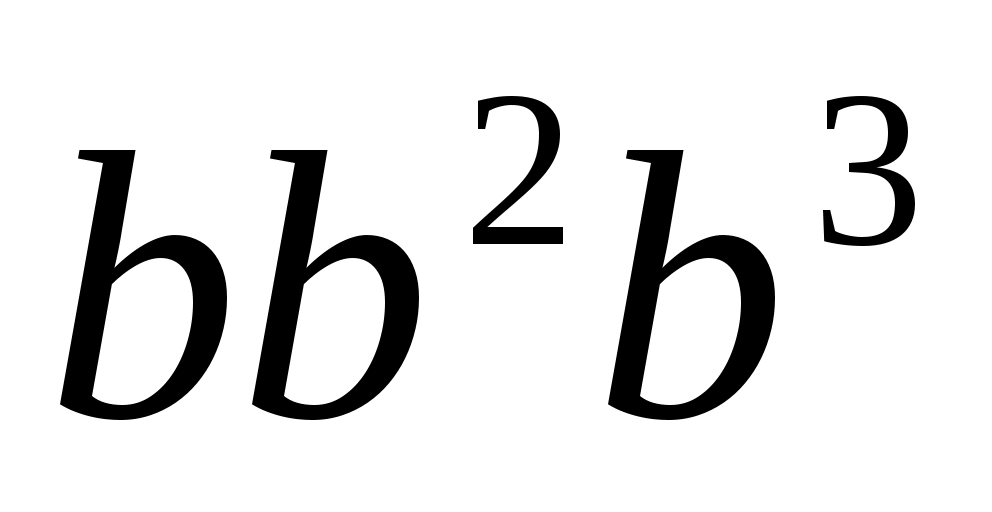 ; в) ; в)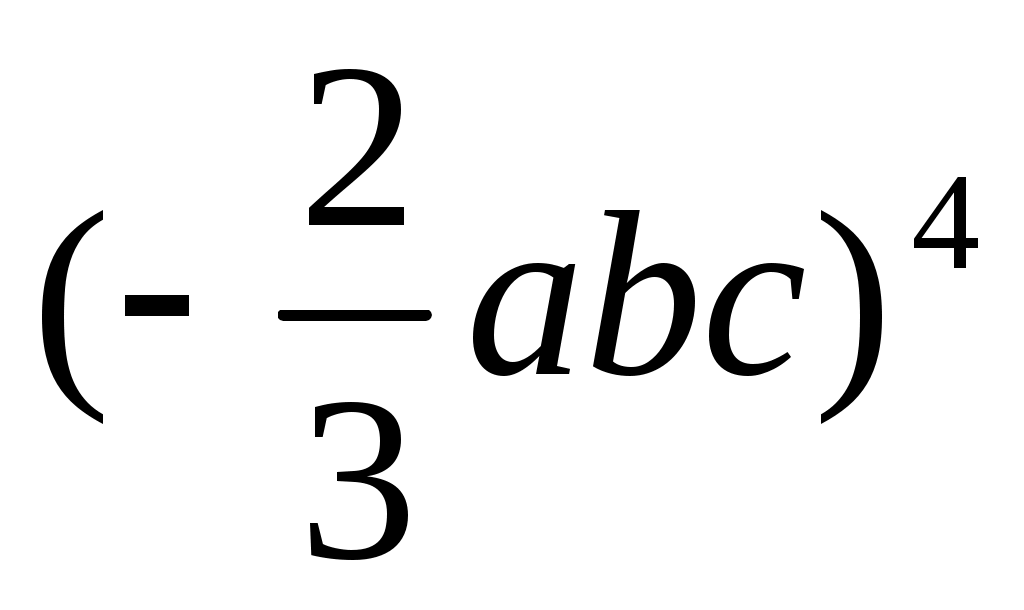 ; ;
б) ; г) ; г)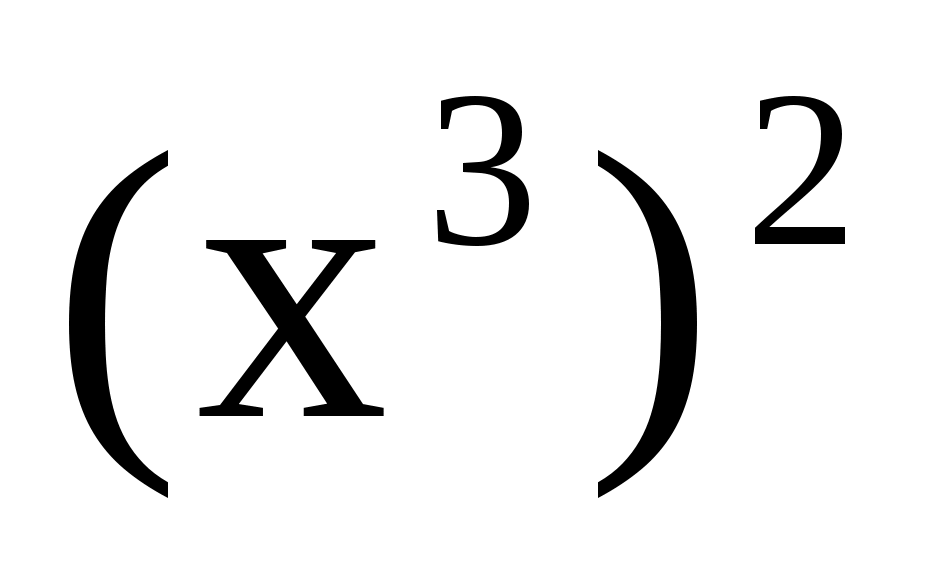 . .
Решение.
а) 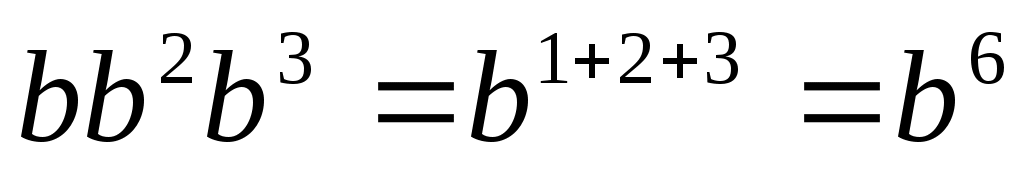 ; ;
б)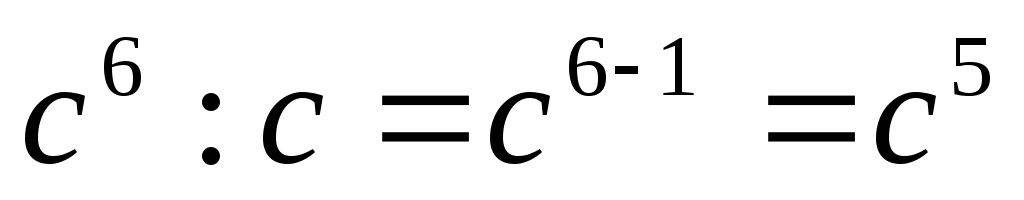 ; ;
в)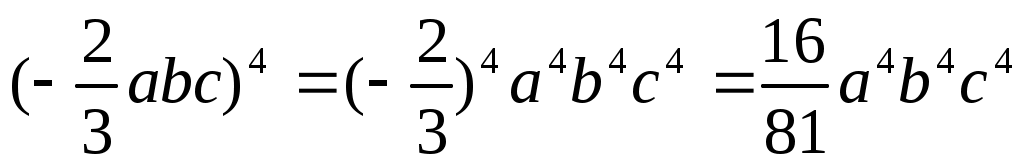 ; ;
г) . .
|
Упростите выражение:
1) 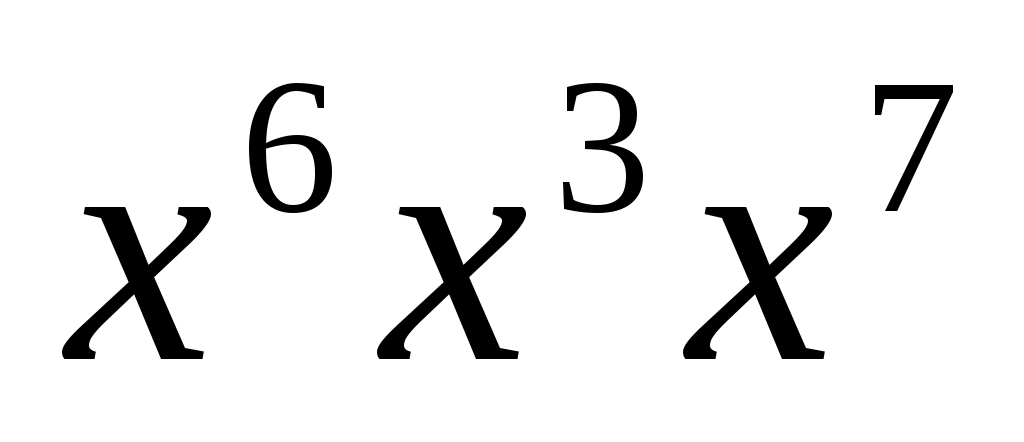 ;2) ;2) 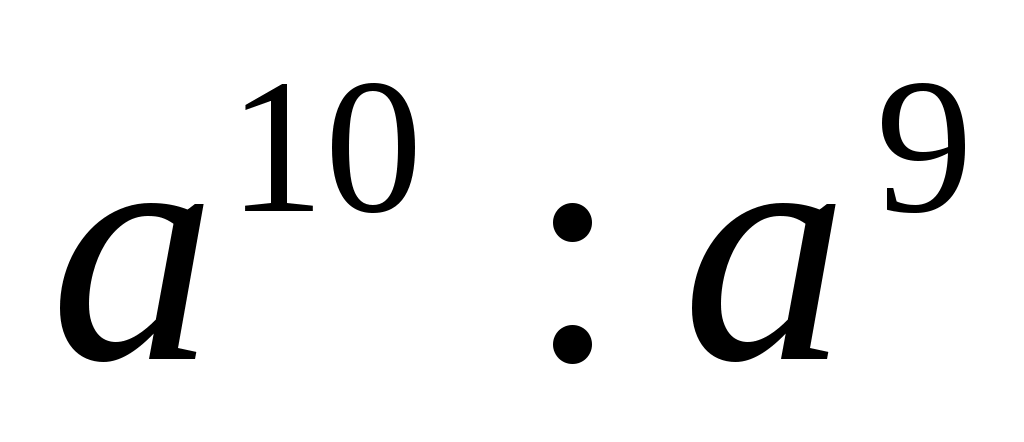 ;3) ;3)  ; ;
4) 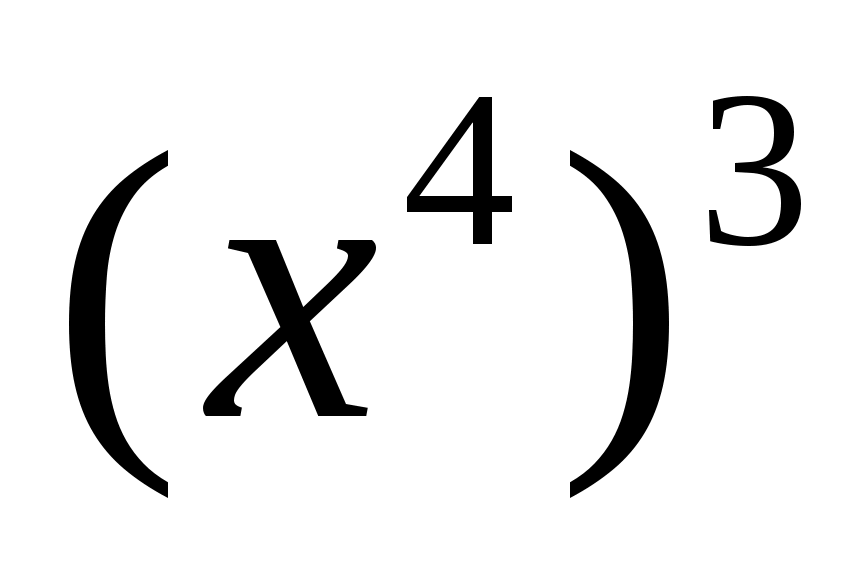 ; 5) ; 5) 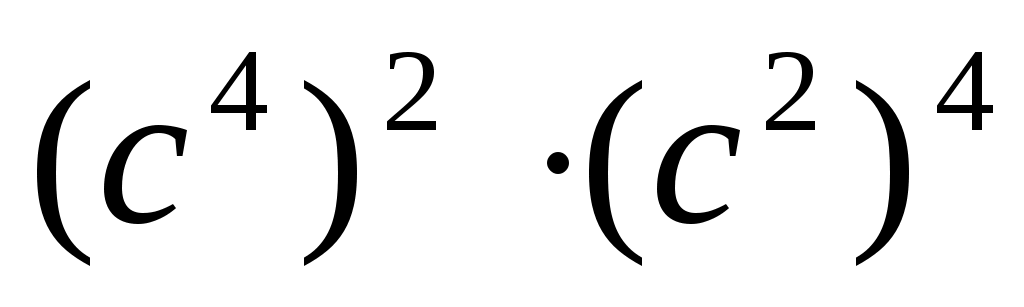 ; ;
6) 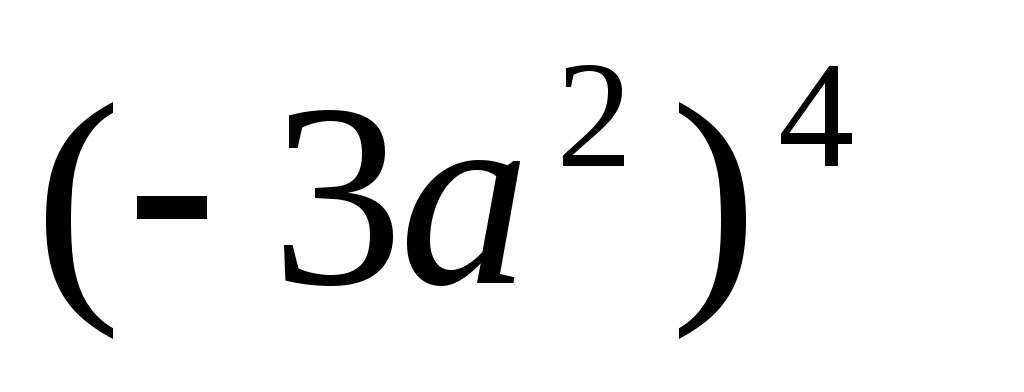 ; 7) ; 7)  ; ;
8) 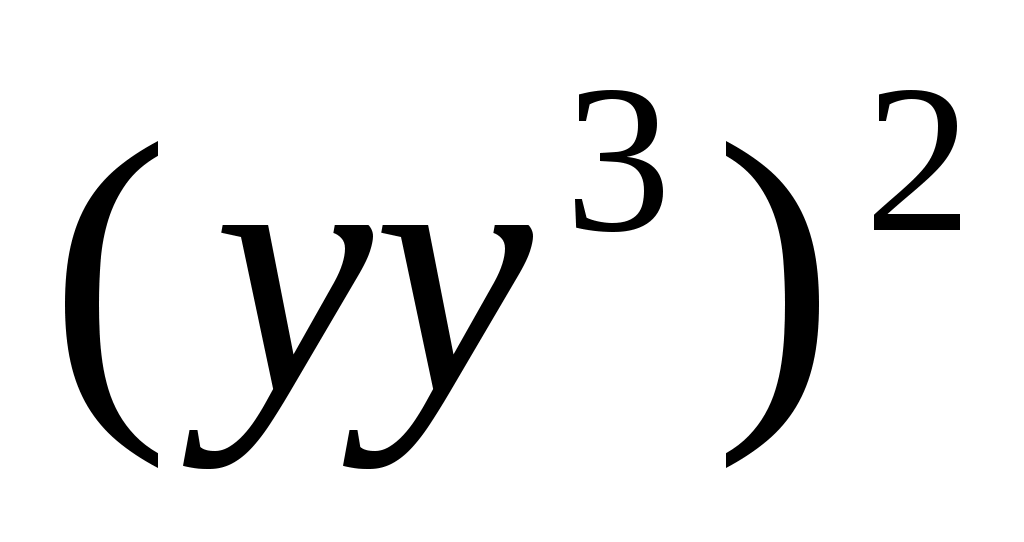 ; 9) ; 9) 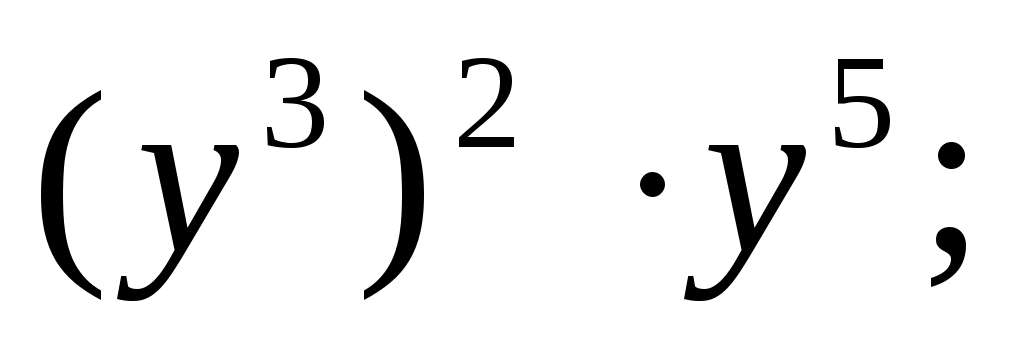
10)  . .
|
Карточка № 5. Разложение многочлена на множители.
Правила
|
Образец
|
Задание
|
1)Вынесение общего
множителя за скобки.
|
Разложите на множители:
а) ; ;
б)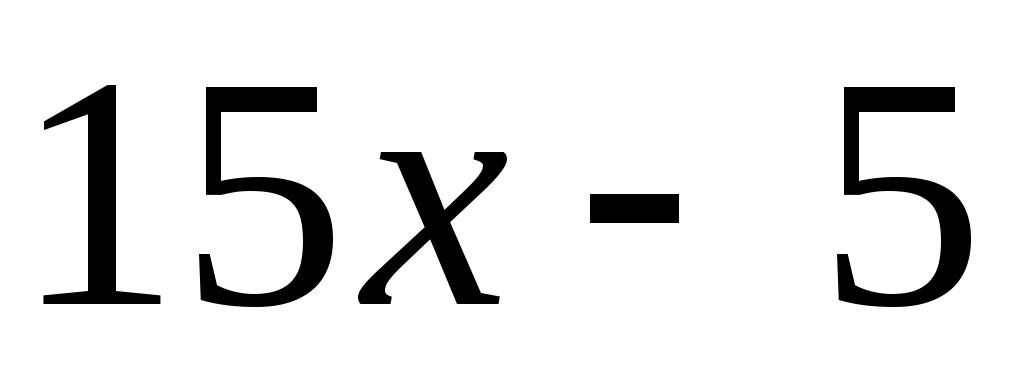 ; ;
в)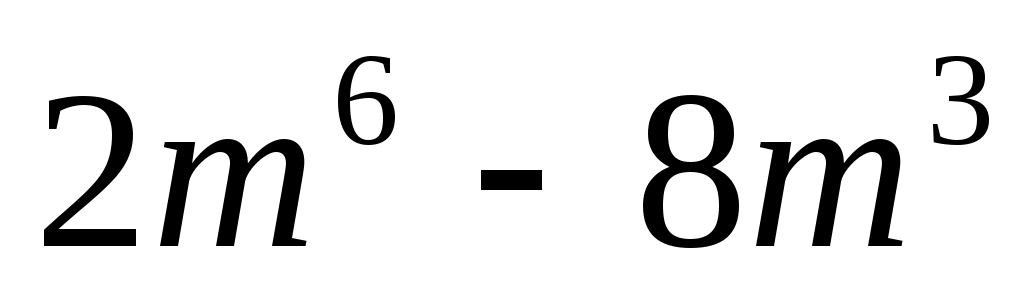 . .
Решение.
а) ; ;
б) ; ;
в)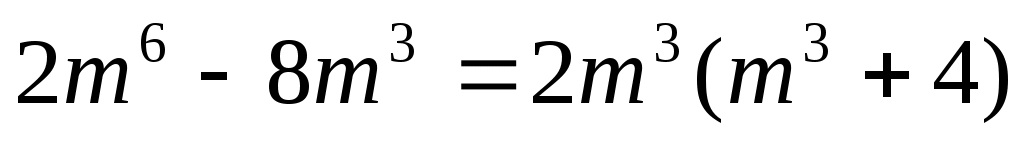 . .
|
Разложите на множители:
а)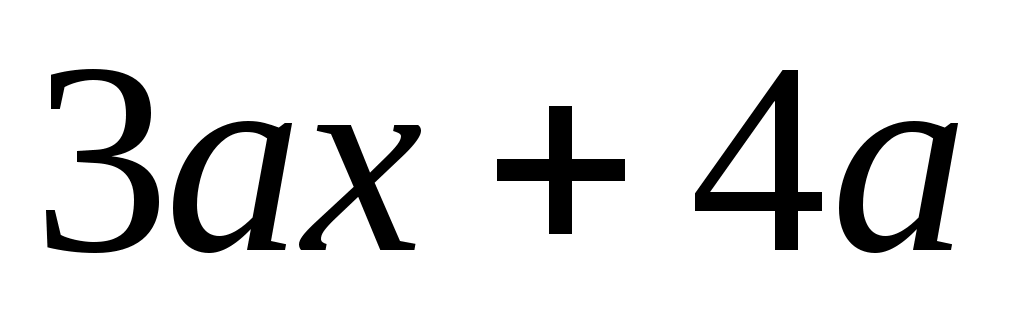 ; б) ; б) ; ;
в)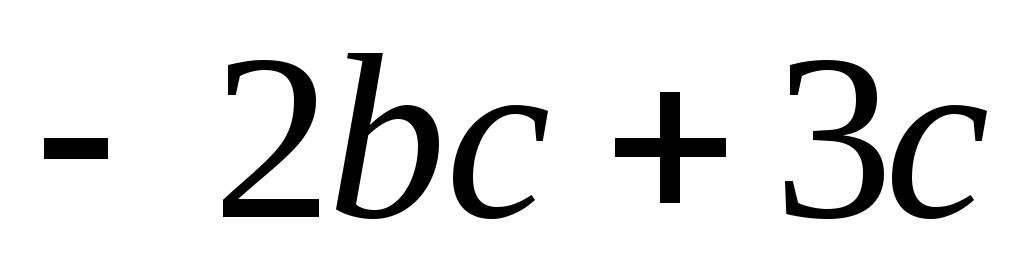 ; г) ; г)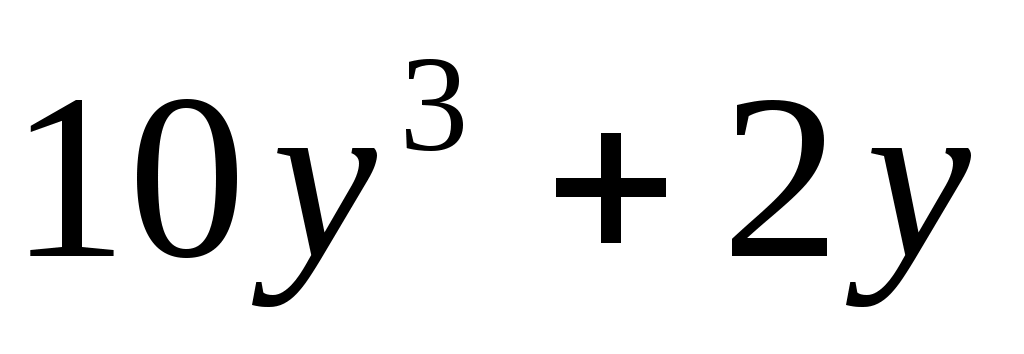 . .
|
2)Способ группировки.
|
Разложите на множители:
а)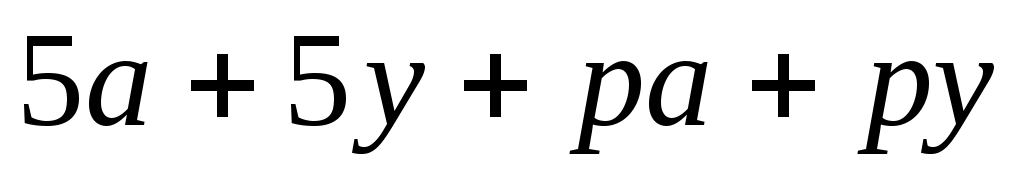 ; ;
б)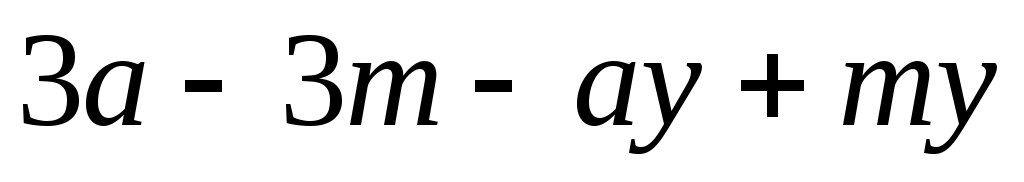 ; ;
Решение.
а)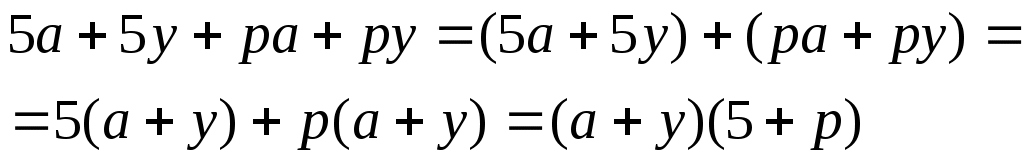 ; ;
б)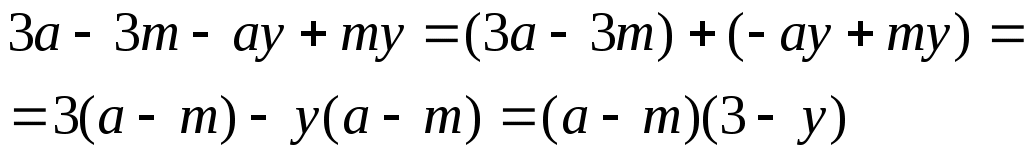 . .
|
Разложите на множители:
а)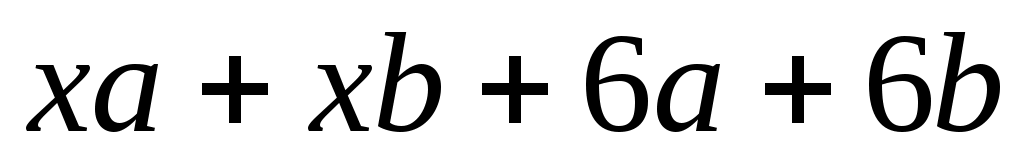 ; ;
б)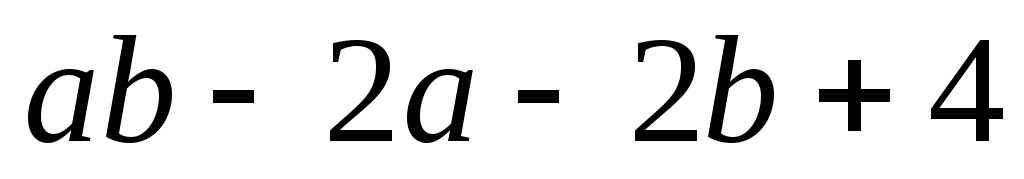 ; ;
в)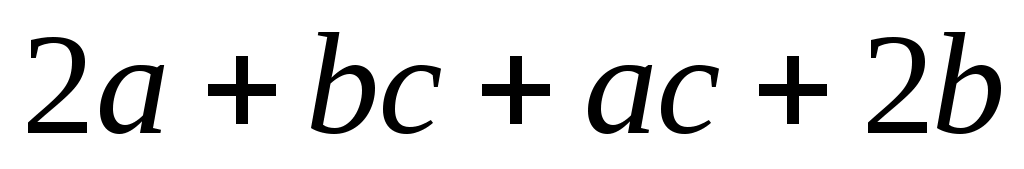 ; ;
г)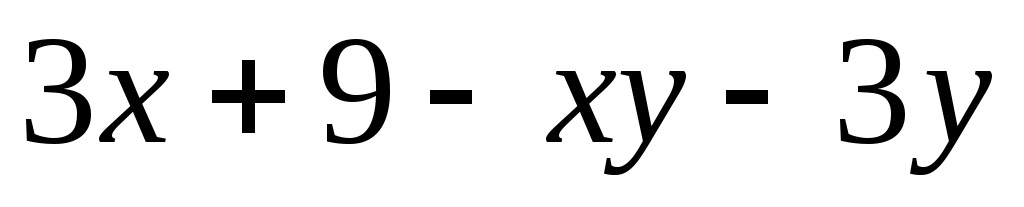 . .
|
Карточка № 6. Формулы сокращенного умножения.
Правила
|
Образец
|
Задание
|
1)Квадрат суммы:
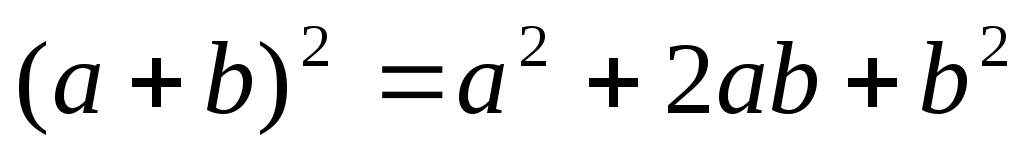
2)квадрат разности:

3)Разность квадратов:

|
Представьте в виде многочлена:
а) 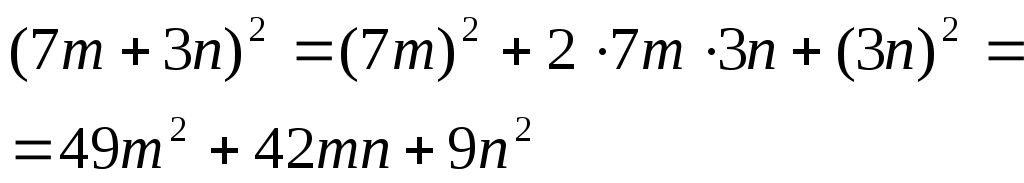 ; ;
б) 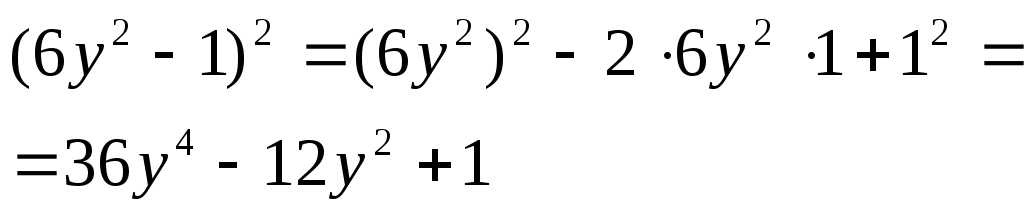 ; ;
в) 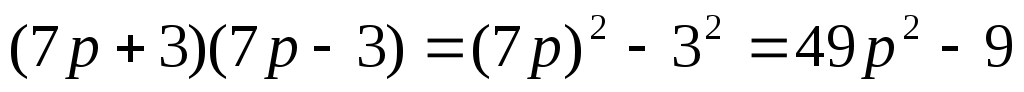
|
Представьте в виде многочлена:
1) 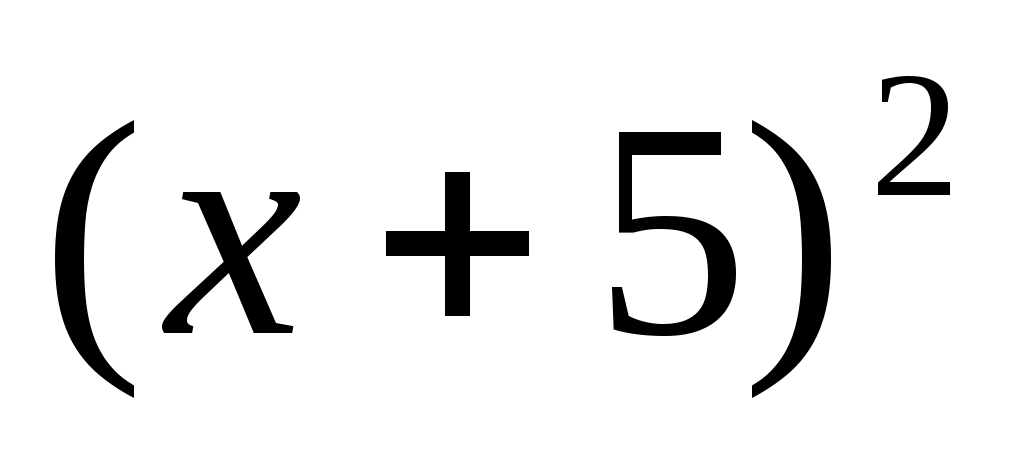 ; 2) ; 2) 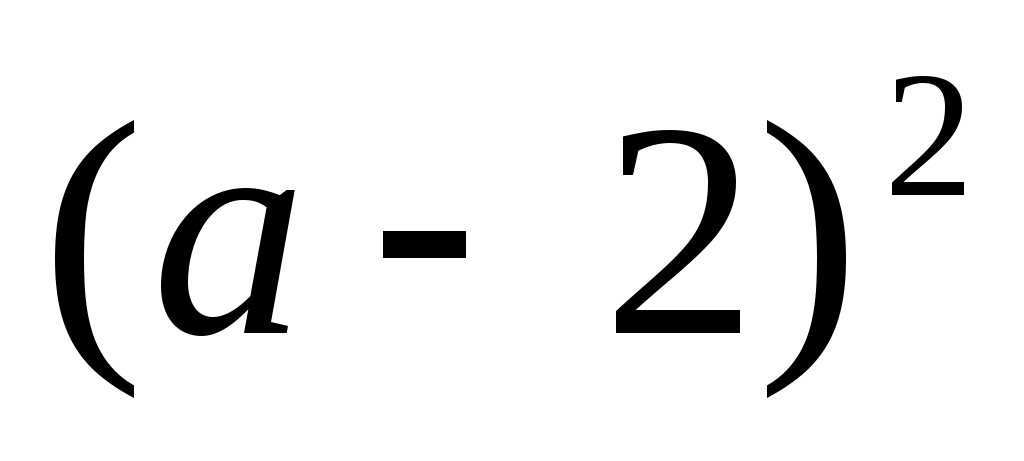 ; 3) ; 3) 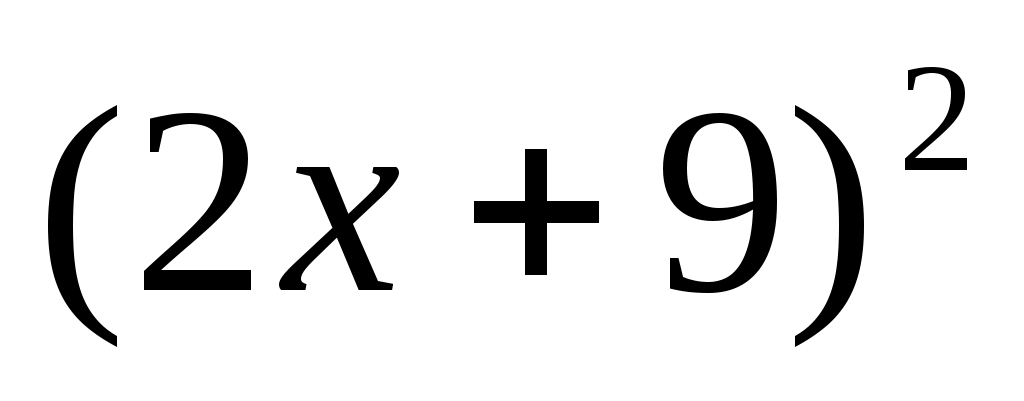 ; ;
4) 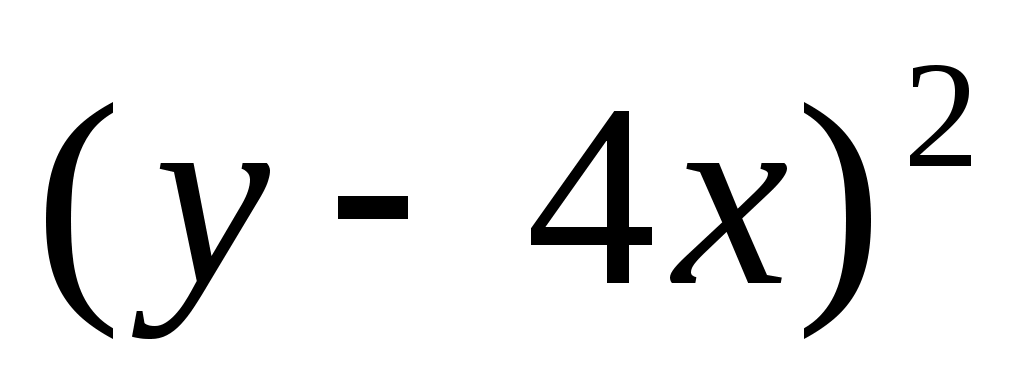 ; 5) ; 5) 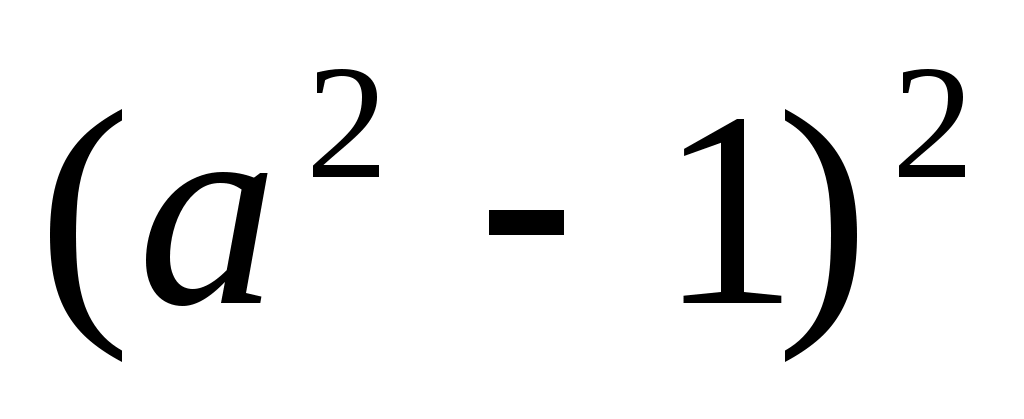 ; ;
6)  ; 7) ; 7) 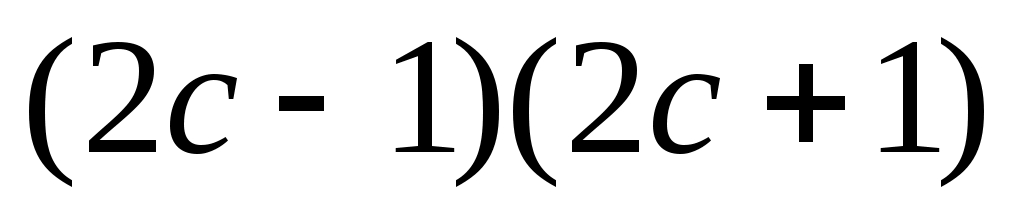 ; ;
8) 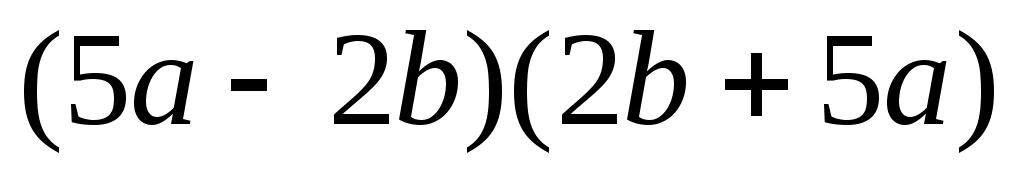 . .
|
Карточка № 7. Решение систем линейных уравнений методом подстановки.
Правило
|
Образец
|
Задание
|
1)Из какого-либо уравнения выразить
одну переменную
через другую.
2)Подставить
полу ченное выражение
для переменной в
другое уравнение и
решить его.
3)Сделать подстановку
найденного значения
переменной и
вычислить значение
второй переменной.
|
Р ешить систему: х + у = 3, ешить систему: х + у = 3,
3х - у = 5.
Решение.
1)Из первого уравнения выражаем х
через у: х = 3 – у.
2)Подставляем это выражение во второе
уравнение вместо х:
3( 3 – у ) – у = 5,
9 – 3у – у = 5,
- 4у = 5 – 9,
- 4у = - 4,
у = 1.
3)Подставляем значение у = 1 в уравнение х х = 3 – у. Если у = 1, то х = 3 – 1 = 2.
Ответ: (2;1).
|
Решить систему:
а  ) х + у = 5, б) х – у = 0, ) х + у = 5, б) х – у = 0,
3х + у = 7; х – 3у = 6;
в  ) у – х = - 3, г) х – у = 8, ) у – х = - 3, г) х – у = 8,
2х + у = 9; 3х – у = - 3;
д  ) у – х = 1, е) х - у = - 3, ) у – х = 1, е) х - у = - 3,
х + у = 3; 2у – х = 6.
|
Карточка № 8. Решение систем линейных уравнений способом сложения.
Правило
|
Образец
|
Задание
|
1)Уравнять модули
коэффициентов при какой-
нибудь переменной.
2)Сложить (вычесть)
почленно уравнения системы.
3)Составить новую систему:
Одно уравнение новое; другое
- одно из старых.
4)Решить новое уравнение и
найти значение одной
переменной.
5)Подставить значение
найденной переменной в
старое уравнение и найти
значение другой переменной.
|
Р ешить систему: х - 4 у = 9, ешить систему: х - 4 у = 9,
3х + 2у = 13.
Решение.

 х - 4у = 9, х - 4у = 9,
3х + 2у = 13; ∙2
 
х - 4у = 9, х - 4у = 9,
6х + 4у = 26; 7х = 35;
  х – 4у = 9, 5 – 4у = 9, х – 4у = 9, 5 – 4у = 9,
х = 5; х = 5;
  
-4у = 9 – 5, -4у = 4, у = -1,
х = 5; х = 5; х = 5.
Ответ: (5;-1).
|
Решить систему:
а  ) 2х + у = 6, б) -х + у = 1, ) 2х + у = 6, б) -х + у = 1,
-4х + 3у = 8; х + у = 3;
в  ) – х + у = - 3, г) х – у = 8, ) – х + у = - 3, г) х – у = 8,
2х + у = 9; 3х – у = - 3;
д  ) 2х – 5у = 9, е) 3х - 2у = 8, ) 2х – 5у = 9, е) 3х - 2у = 8,
4х + 2у = 6; 6х + 3у = 9.
| |
 Скачать 173 Kb.
Скачать 173 Kb.
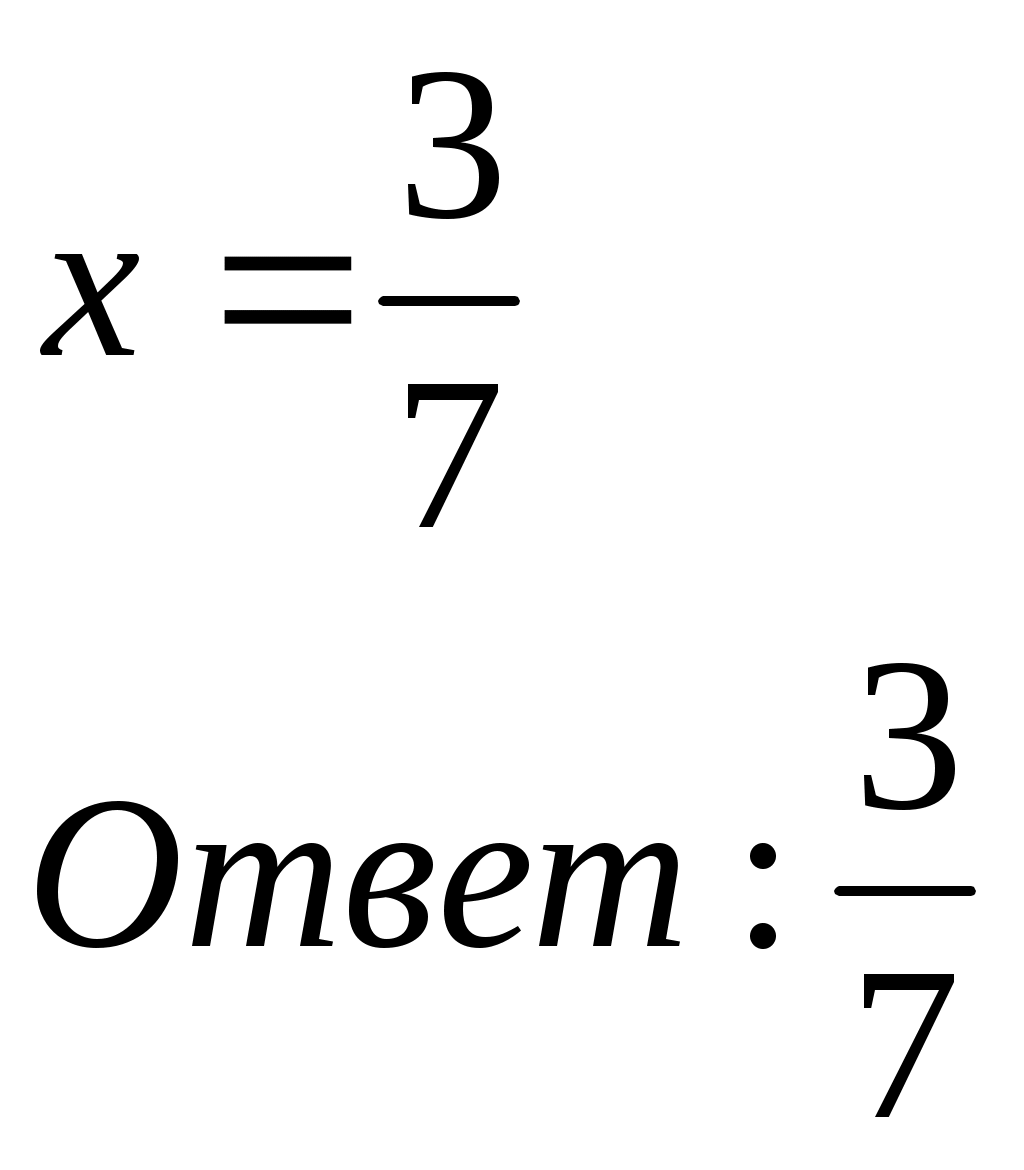


 ешить систему: х + у = 3,
ешить систему: х + у = 3,

