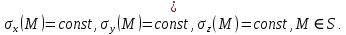Приложение криволинейного интеграла второго рода. Курсовая. Институт физики, математики, цифровых и нанотехнологий
 Скачать 135.46 Kb. Скачать 135.46 Kb.
|
|
МИНПРОСВЕЩЕНИЕ РОССИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ ИМ.М.АКМУЛЛЫ» ИНСТИТУТ ФИЗИКИ, МАТЕМАТИКИ, ЦИФРОВЫХ И НАНОТЕХНОЛОГИЙ Кафедра математики и статистики Направление 03.03.01 – Прикладная математика и физика Модуль «Математика» Курс III ФИО ПРИЛОЖЕНИЕ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА ВТОРОГО РОДА КУРСОВАЯ РАБОТА по дисциплине «Математика» Научный руководитель: № регистрации по журналу учета курсовых работ_________________________________________ Дата защиты________________________________________________ Оценка_____________________________________________________ Подпись научного руководителя________________________________ Уфа 2022 СОДЕРЖАНИЕ ВВЕДЕНИЕ 3 Глава 1. Криволинейные интегралы второго рода. 4 1.1.Определение криволинейного интеграла второго рода 4 1.2.Криволинейный интеграл по замкнутому контуру. Формула Грина. Формула Стокса. 7 1.3.Решение задач 11 ЗАКЛЮЧЕНИЕ 15 ЛИТЕРАТУРА 16 ВВЕДЕНИЕ Областью интегрирования определённого интеграла является отрезок на прямой; двойного интеграла – некоторая область в плоскости; тройного – некоторая область в пространстве. Однако существуют интегралы, областью интегрирования которых является кривая, расположенная в плоскости или в пространстве. Такие интегралы называются криволинейными интегралами. Аппарат криволинейных интегралов значительно расширяет возможности приложений математического анализа к решению задач из механики и физики. Особенно большое значение криволинейные интегралы имеют в теории поля и в теории функции комплексной переменной. Все важные математические понятия получены в связи с исследованием тех или иных практических проблем. Практические задачи также привели к различным криволинейным интегралам. Целью курсовой работы является рассмотрение криволинейного интеграла второго рода. Для достижения цели нужно выполнить задачи: рассмотрение определения криволинейного интеграла второго рода; изучение формулы Грина и формулы Стокса; вычисление некоторых криволинейных интегралов. Глава 1. Криволинейные интегралы второго рода. Определение криволинейного интеграла второго рода Пусть 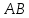 — кривая на плоскости или в пространстве. Точка — кривая на плоскости или в пространстве. Точка  — начало кривой, точка — начало кривой, точка 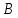 — конец кривой. На множестве — конец кривой. На множестве  точек кривой точек кривой 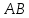 зададим функцию зададим функцию  зависящую от двух или трёх переменных (в зависимости от размерности кривой). Построим разбиение кривой зависящую от двух или трёх переменных (в зависимости от размерности кривой). Построим разбиение кривой 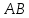 точками точками  , где , где  так, чтобы так, чтобы  . Множество таких точек обозначим буквой T. Пусть . Множество таких точек обозначим буквой T. Пусть  — частичная дуга кривой — частичная дуга кривой 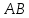 , соединяющая точки , соединяющая точки  . Для каждого . Для каждого 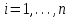 обозначим через обозначим через  длину этой дуги. Тогда диаметром разбиения длину этой дуги. Тогда диаметром разбиения  будем называть величину будем называть величину  . На каждой дуге . На каждой дуге  выберем произвольным образом точку выберем произвольным образом точку  Пусть точка Пусть точка  имеет координаты имеет координаты 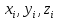 . Будем традиционно обозначать . Будем традиционно обозначать  . Составим сумму . Составим сумму
которую будем называть интегральной суммой, соответствующей заданному разбиению.
Определение. Криволинейным интегралом второго рода функции 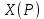 по кривой по кривой 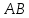 по координате по координате  называется предел называется предел  при условии, что этот предел не зависит от разбиений при условии, что этот предел не зависит от разбиений  и от выбора точек и от выбора точек  Обозначение: Обозначение:  . . Аналогично определяются криволинейные интегралы второго рода  и и  по координатам по координатам  для функций для функций  определённых на множестве точек кривой определённых на множестве точек кривой 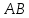 . Полное выражение для криволинейного интеграла второго рода определяется как сумма криволинейных интегралов по каждой координате: . Полное выражение для криволинейного интеграла второго рода определяется как сумма криволинейных интегралов по каждой координате:
Рассмотрим свойства криволинейного интеграла второго рода. 1  . Если . Если  на на  то то  . .2  . Если начало и конец кривой поменять местами, то значение криволинейного интеграла второго рода поменяет знак, то есть . Если начало и конец кривой поменять местами, то значение криволинейного интеграла второго рода поменяет знак, то есть  . .3  . Если точка . Если точка  лежит на кривой лежит на кривой 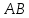 , то , то  4  . .  5  . .  где где 6  . Пусть . Пусть  — касательный вектор к кривой в точке — касательный вектор к кривой в точке  , причём его направление соответствует ориентации кривой, то есть указывает направление движения от начала к концу кривой. При этом длина вектора , причём его направление соответствует ориентации кривой, то есть указывает направление движения от начала к концу кривой. При этом длина вектора  равна единице. Тогда, если вектор равна единице. Тогда, если вектор  образует с осями координат углы образует с осями координат углы  , то координаты этого вектора будут равны ( , то координаты этого вектора будут равны ( (направляющие косинусы вектора). В этих обозначениях криволинейный интеграл второго рода можно выразить через криволинейный интеграл первого рода по формуле (направляющие косинусы вектора). В этих обозначениях криволинейный интеграл второго рода можно выразить через криволинейный интеграл первого рода по формуле
7  . Пусть функции . Пусть функции  служат координатами вектора служат координатами вектора  В этом случае говорят, что на кривой В этом случае говорят, что на кривой 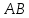 задано векторное поле задано векторное поле  . Тогда равенство (3) можно записать в виде . Тогда равенство (3) можно записать в виде
Здесь точкой обозначено скалярное произведение векторов. 8  . Из равенства (4) следует формула для оценки криволинейного интеграла второго рода . Из равенства (4) следует формула для оценки криволинейного интеграла второго рода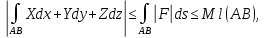 Если 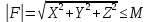 на на 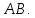 9  . Физическая интерпретация. Пусть . Физическая интерпретация. Пусть  — силовое поле, действующее на материальную точку, которая движется по траектории, совпадающей с кривой — силовое поле, действующее на материальную точку, которая движется по траектории, совпадающей с кривой 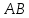 . Тогда величина криволинейного интеграла . Тогда величина криволинейного интеграла  равна работе силового поля равна работе силового поля  по перемещению точки. по перемещению точки.Если кривая AB в пространстве задана параметрически уравнениями  то формула для вычисления полного криволинейного интеграла (2) имеет вид
Если кривая плоская, то формула (5) примет вид
Если кривая задана графиком функции 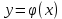 при при 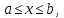 то в качестве параметра можно принять переменную то в качестве параметра можно принять переменную  и тогда формула (6) примет вид и тогда формула (6) примет вид
Аналогично, если кривая AB является графиком функции  при при  , то параметром будет служить переменная y и тогда формула (6) примет вид , то параметром будет служить переменная y и тогда формула (6) примет вид
Криволинейный интеграл по замкнутому контуру. Формула Грина. Формула Стокса. Определение. Если начало и конец кривой совпадают, то кривая называется замкнутым контуром (часто просто контуром). Для определения криволинейного интеграла по замкнутому контуру в качестве точки, определяющей начало и конец кривой, можно выбрать любую лежащую на ней точку. При этом требуется задать направление её обхода, которое называется ориентацией контура. Определение. Пусть 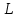 — замкнутый контур, лежащий на координатной плоскости — замкнутый контур, лежащий на координатной плоскости  Замкнутый контур Замкнутый контур 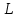 называется положительно ориентированным, если на нём определён обход в направлении, при котором ограниченная контуром область остаётся слева. Иначе говоря, обход контура называется положительно ориентированным, если на нём определён обход в направлении, при котором ограниченная контуром область остаётся слева. Иначе говоря, обход контура 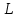 производится против часовой стрелки. В противном случае контур называется отрицательно ориентированным. На рис. 2 ориентация контура показана стрелками. производится против часовой стрелки. В противном случае контур называется отрицательно ориентированным. На рис. 2 ориентация контура показана стрелками.
Для замкнутого контура как и для обычной кривой может быть определён криволинейный интеграл, который в этом случае часто обозначается 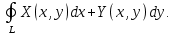 Если обозначать через Если обозначать через  один и тот же контур, ориентированный положительно и отрицательно, то из свойств криволинейного интеграла можно вывести равенство один и тот же контур, ориентированный положительно и отрицательно, то из свойств криволинейного интеграла можно вывести равенство то есть при смене ориентации контура величина криволинейного интеграла меняет знак. Теорема 1 (формула Грина). Пусть замкнутый контур 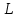 ориентирован положительно и ограничивает область ориентирован положительно и ограничивает область  на плоскости на плоскости  . Пусть, кроме того, на множестве . Пусть, кроме того, на множестве  вместе с его границей вместе с его границей 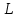 определены функции определены функции  и и  , которые непрерывны в замыкании , которые непрерывны в замыкании  вместе с их частными производными вместе с их частными производными  . Тогда справедливо равенство . Тогда справедливо равенство
Следствие 1. Если в равенстве (9) взять  , то получим , то получим  Аналогично, если в равенстве (9) взять  , то , то  Определение. Поверхностью, заданной в явном виде, называется множество точек с координатами  удовлетворяющими условиям удовлетворяющими условиям
где функция  определена и непрерывна в некоторой области определена и непрерывна в некоторой области  на координатной плоскости на координатной плоскости  . Если функция . Если функция  дифференцируема в дифференцируема в  , то поверхность называется гладкой. , то поверхность называется гладкой. Определение. Выбор одной из двух сторон (верхней или нижней) поверхности, заданной условием (10), называется ориентацией поверхности. Если на поверхности выбрана верхняя (нижняя) сторона, то будем эту поверхность называть положительно (отрицательно) ориентированной относительно оси  . .Для гладкой поверхности в каждой её точке можно построить нормальный вектор, который перпендикулярен касательной плоскости, проведённой к поверхности через эту точку. Тогда ориентацию поверхности удобно задавать указанием направления нормального вектора: верхней стороне соответствует нормальный вектор, который образует острый угол с координатной осью  , соответственно для нижней стороны поверхности нормальный вектор образует тупой угол с осью , соответственно для нижней стороны поверхности нормальный вектор образует тупой угол с осью  . В тех точках поверхности, в которых нормальный вектор перпендикулярен оси . В тех точках поверхности, в которых нормальный вектор перпендикулярен оси  , ориентацию относительно оси , ориентацию относительно оси  будем считать неопределённой. Если γ — угол между нормальным вектором и осью будем считать неопределённой. Если γ — угол между нормальным вектором и осью  , то ориентацию поверхности относительно оси , то ориентацию поверхности относительно оси  обозначим так: обозначим так: Определение. Образ границы множества  при отображении функцией при отображении функцией  называется границей или краем поверхности, заданной условиями (10). Граница поверхности называется границей или краем поверхности, заданной условиями (10). Граница поверхности  обозначается обозначается  . . Аналогичные определения формулируются для случая, когда поверхность задаётся при помощи функции  или функции или функции  , определённой и непрерывной в некоторой области , определённой и непрерывной в некоторой области  соответствующей координатной плоскости. В этих случаях следует говорить о положительной или отрицательной ориентации поверхности относительно оси соответствующей координатной плоскости. В этих случаях следует говорить о положительной или отрицательной ориентации поверхности относительно оси 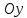 или оси или оси  соответственно, которые будем обозначать соответственно, которые будем обозначать  Все поверхности будем считать явно заданными и гладкими. Будем предполагать также, что для любой поверхности её ориентация относительно каждой оси от точки к точке не меняется, возможно исключая точки, лежащие на границе поверхности:
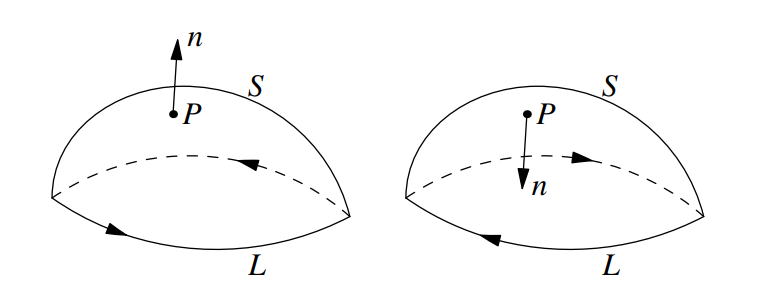
где 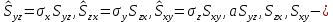 площади проекций ориентированной поверхности S на координатные плоскости площади проекций ориентированной поверхности S на координатные плоскости 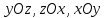 соответственно. соответственно. Пусть  — ограниченная ориентированная поверхность в пространстве, причём границей этой поверхности является замкнутый контур — ограниченная ориентированная поверхность в пространстве, причём границей этой поверхности является замкнутый контур 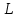 . .Определение. Будем говорить, что ориентация поверхности S является согласованной с ориентацией контура 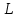 , если при наблюдении с конца нормального вектора n к поверхности обход контура L производится против часовой стрелки (см. рис. 3). , если при наблюдении с конца нормального вектора n к поверхности обход контура L производится против часовой стрелки (см. рис. 3).
Замечание. Правило, по которому согласуются ориентации поверхности и её границы, называется также «правилом штопора»: если вращать ручку штопора по направлению, задаваемому ориентацией контура L, то штопор будет двигаться поступательно в направлении нормального вектора n. Теорема 2. Пусть ориентация поверхности S согласована с ориентацией контура 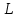 , функции , функции 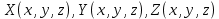 определены и непрерывны вместе со своими частными производными на определены и непрерывны вместе со своими частными производными на  . Тогда выполняется равенство . Тогда выполняется равенство
Формула (13) называется формулой Стокса. В некоторых случаях эта формула существенно упрощает вычисление криволинейного интеграла. Решение задач Задача 1. Вычислить криволинейный интеграл  , где , где  — ломаная, соединяющая точки — ломаная, соединяющая точки 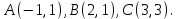 Для этого разобьём интеграл на два: Для этого разобьём интеграл на два: Отрезок Отрезок 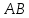 является частью прямой заданной уравнением является частью прямой заданной уравнением 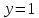 , причём , причём  . Поэтому по формуле (7) . Поэтому по формуле (7) Отрезок  является частью прямой заданной уравнением является частью прямой заданной уравнением  , причём , причём  . Поэтому по формуле (7) . Поэтому по формуле (7) В итоге значение всего криволинейного интеграла по ломаной  равно равно  . . Если кривая задана уравнением в полярных координатах, то формула (6) также может быть применена, при этом параметром будет служить полярный угол  или полярный радиус или полярный радиус  Задача 2. Вычислить криволинейный интеграл  , если , если 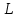 — треугольник с вершинами в точках — треугольник с вершинами в точках 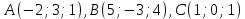 . Ориентация контура соответствует порядку перечисления вершин треугольника. Используем для вычисления формулу Стокса. Пусть . Ориентация контура соответствует порядку перечисления вершин треугольника. Используем для вычисления формулу Стокса. Пусть  — часть плоскости, расположенной внутри треугольника — часть плоскости, расположенной внутри треугольника  . Тогда по формуле (13) криволинейный интеграл сводится к поверхностному . Тогда по формуле (13) криволинейный интеграл сводится к поверхностному
Из аналитической геометрии известно, что векторное произведение 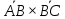 имеет координаты численно равные площадям проекций параллелограмма, построенного на векторах имеет координаты численно равные площадям проекций параллелограмма, построенного на векторах  . При этом вектор . При этом вектор 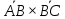 является нормальным для плоскости, а его направление соответствует ориентации поверхности, согласованной с ориентацией треугольника является нормальным для плоскости, а его направление соответствует ориентации поверхности, согласованной с ориентацией треугольника 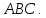 Используя обозначения формул (12), этот факт можно записать в виде равенства Используя обозначения формул (12), этот факт можно записать в виде равенства
Найдём координаты векторов  , а также их векторное произведение: , а также их векторное произведение: 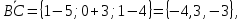 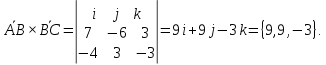 Тогда из формул ( 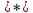 ) находим ) находим  Используя равенства (  ) и (12), определяем значение поверхностного интеграла ) и (12), определяем значение поверхностного интеграла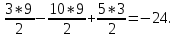 Задача 3. Вычислить криволинейный интеграл 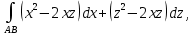 где где  дуга параболы дуга параболы 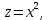 пробегаемая от точки пробегаемая от точки 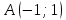 до точки до точки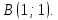 Сделаем рисунок.
 ЗАКЛЮЧЕНИЕ Проблема изучения криволинейного интеграла второго рода является весьма актуальной. Опираясь на поставленные задачи, в работе удалось раскрыть основные аспекты теории и приложений криволинейного интеграла второго рода. Изначально были сформулированы основные теоретические сведения, включающие определение криволинейного интеграла второго рода, его свойства и условие существования. На основе рассмотренных теоретических сведений были рассмотрены приложения и теоремы (условия независимости криволинейного интеграла от пути интегрирования). Для получения полной картины были рассмотрены основные задачи и приложения криволинейного интеграла второго рода. В конце курсовой работы приводятся примеры решений задач Необходимо понимать, что изучение криволинейного интеграла второго рода имеет высочайшее значение не только в математическом анализе, но и других сферах науки, таких, как физика, геометрия, экономика. Ведь часто на практике возникают задачи, в которых использование свойств и приложений криволинейного интеграла второго рода значительно упрощает процесс нахождения результата. ЛИТЕРАТУРА Аксёнов А.П. Математический анализ (Определенный интеграл. Несобственные интегралы. Приложения определенного интеграла). – СПб.: Нестор, 2000. Гаврилов В.Р., Иванова Е.Е., Морозова В.Д. Кратные и криволинейные интегралы. Элементы теории поля: Учеб. для вузов / Под ред. В.С. Зарубина, А.П. Крищенко. – 2-е изд., стереотип. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2003. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 3. – изд. 4-е, – М.: Наука, главная редакция физико-математической литературы, 1966. Кудрявцев Л.Д. Краткий курс математического анализа. Т. 2. Дифференциальное и интегральное исчисления функций многих переменных. Гармонический анализ: Учебник. – 3-е изд., перераб. – М.:ФИЗМАТЛИТ, 2005. Ильин В. А., Позняк Э. Г. Основы математического анализа. Часть 1. Учеб.: Для вузов. – 7-е изд. – М.: ФИЗМАТЛИТ, 2005 Кудрявцев Л. Д., Кутасов А. Д., Чехлов В. И., Шабунин М. И. Сборник задач по математическому анализу. Том 3. Функции нескольких переменных: Учеб. пособие/ Под ред. Л. Д. Кудрявцева. – 2-е изд., перераб. – М.:ФИЗМАТЛИТ, 2003. Федоров, Д. Л. Криволинейные интегралы второго рода : учебно-методическое пособие / Д. Л. Федоров, Т. С. Тинюкова, Л. П. Сметанина. – Ижевск : Удмуртский университет, 2021. – 80 с. – ISBN 978-5-4312-0953-6. – EDN WYGFPP. Шведенко, С. В. К определению криволинейных интегралов и доказательству формулы Грина / С. В. Шведенко // Математическое образование. – 2013. – № 4(68). – С. 58-69. – EDN SAFOYD. |



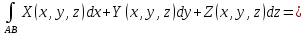








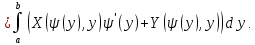


 ,
,