расчетно графическая работа по физике механика. Юрлов Р.В. РГР1. Институт нефтепереработки и нефтехимии фгбоу во угнту в г. Салавате
 Скачать 92.16 Kb. Скачать 92.16 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Уфимский государственный нефтяной технический университет» (ФГБОУ ВО УГНТУ) Институт нефтепереработки и нефтехимии ФГБОУ ВО УГНТУ в г. Салавате Кафедра «Информационных технологий» Физика РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА Классическая механика ИнТех- 09.03.01 – 1.01.09 РГР Исполнитель: студент гр. БАБз - 22-21 Юрлов Р. В. Руководитель: ассистент Г.Ф. Шаяхметов Салават 2023 1.9. По краю равномерно вращающийся с угловой скоростью  платформы идет человек и обходит платформу за время платформы идет человек и обходит платформу за время 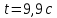 . Каково наибольшее ускорение, а движения человека относительно Земли? Принять радиус платформы . Каково наибольшее ускорение, а движения человека относительно Земли? Принять радиус платформы  Дано: 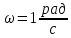 ; ; 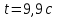 ; ;  Найти: 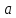 Решение. По определению центростремительное ускорение: 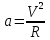 . .Так как человек обходит платформу по краю, то его скорость относительно платформы: 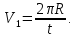 Если человек обходит платформу по направлению вращения, скорость человека относительно земли будет максимальна:  где 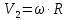 – скорость вращения края платформы, м/с. – скорость вращения края платформы, м/с.Подставим  Подставляем  Проверим размерности расчетных формул 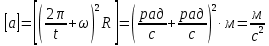 Подставляя числовые значения получим ответ  . .Ответ: 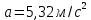 1.19. На сколько переместится относительно берега лодка длиной 1 =3,5м и массой m1 = 200кг, если стоящий на корме человек массой т2 = 80кг переместится на нос лодки. Считать лодку расположенной перпендикулярно берегу. Дано: 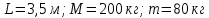 Найти: 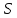 Р  ешение. ешение.Систему человек – лодка относительно горизонтального направления можно рассматривать как замкнутую. Согласно следствию из закона сохранения импульсов, внутренние силы замкнутой системы тел не могут изменить положение центра масс системы. Применяя это следствие к системе человек – лодка, можно считать, что при перемещении человека по лодке центр масс системы не изменит своего положения, т.е. останется на прежнем расстоянии от берега. Пусть центр масс системы человек- лодка находится на вертикали, проходящей в начальный момент через точку 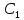 лодки, а после перемещения лодки – через другую ее точку лодки, а после перемещения лодки – через другую ее точку 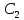 . Так как эта вертикаль неподвижна относительно берега, то искомое перемещение . Так как эта вертикаль неподвижна относительно берега, то искомое перемещение 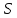 лодки относительно берега равно перемещению лодки относительно вертикали. А это последнее легко определить по перемещению центра масс лодки относительно берега равно перемещению лодки относительно вертикали. А это последнее легко определить по перемещению центра масс 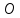 лодки. Как видно из рисунка, в начальный момент точка лодки. Как видно из рисунка, в начальный момент точка 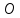 находится на расстоянии находится на расстоянии  слева от вертикали, а после перехода человека – на расстоянии слева от вертикали, а после перехода человека – на расстоянии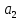 справа от вертикали. Следовательно, искомое перемещение лодки: справа от вертикали. Следовательно, искомое перемещение лодки: Для определения  воспользуемся тем, что результирующий момент сил, действующих на систему относительно горизонтальной оси, перпендикулярной продольной оси лодки, равен нулю. воспользуемся тем, что результирующий момент сил, действующих на систему относительно горизонтальной оси, перпендикулярной продольной оси лодки, равен нулю. Поэтому для начального положения системы 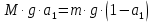 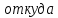  После перемещения лодки  откуда 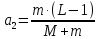 Подставив значения получим  Проверим размерности расчетных формул  Подставляя числовые значения получим ответ 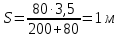 Ответ: 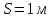 1.29. Из орудия, не имеющего противооткатного устройства, производилась стрельба в горизонтальном направлении. Когда орудие было неподвижно закреплено, снаряд вылетел со скоростью  , а когда орудию дали возможность свободно откатываться назад, снаряд вылетел со скоростью , а когда орудию дали возможность свободно откатываться назад, снаряд вылетел со скоростью 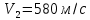 . С какой скоростью откатилось при этом орудие? . С какой скоростью откатилось при этом орудие?Дано:  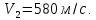 Найти: 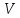 Р  ешение ешениеИз закона сохранения импульса получаем, что импульс снаряда во втором случае равен импульсу установки: 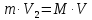 Откуда искомая скорость равна  Из закона сохранения энергии получаем, что кинетическая энергия установки равна разности кинетической энергии снаряда в первом и во втором случае: 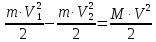 откуда  подставляем 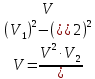 откуда 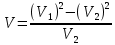 Проверим размерности расчетных формул  Подставляя числовые значения получим ответ  Ответ:  1.39. Цепь длиной 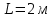 лежит на столе, одним концом свисая со стола. Если длина свешивающейся части превышает лежит на столе, одним концом свисая со стола. Если длина свешивающейся части превышает  , то цепь соскальзывает со стола. Определить скорость , то цепь соскальзывает со стола. Определить скорость 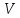 цепи в момент ее отрыва от стола. цепи в момент ее отрыва от стола.Дано: 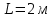 ; ; Найти: 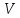 Решение. 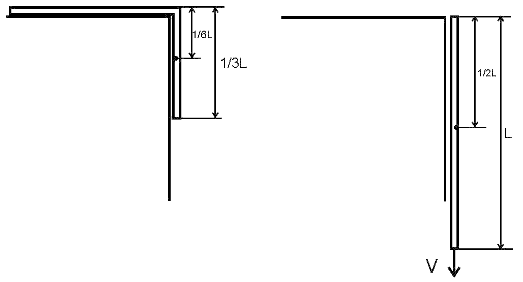 Пусть масса всей цепи будет 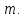 Так как вначале свисает Так как вначале свисает 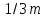 , а ее центр тяжести находится на расстоянии , а ее центр тяжести находится на расстоянии 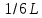 от поверхности стола. от поверхности стола. Поэтому начальная потенциальная энергия 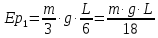 . . После того как цепь полностью соскользнет, ее масса будет равна 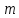 , а ее центр тяжести находится на расстоянии , а ее центр тяжести находится на расстоянии 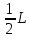 от поверхности стола. от поверхности стола. Поэтому конечная потенциальная энергия 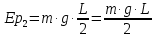 Разность потенциальных энергий равна кинетической энергии цепи 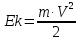 поэтому 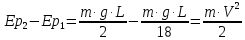 откуда 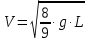 Проверим размерности расчетных формул  Подставляя числовые значения получим ответ  Ответ: 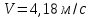 1.49. К краю стола прикреплен блок. Через блок перекинута невесомая и нерастяжимая нить, к концам которой прикреплены грузы. Один груз движется по поверхности стола, а другой - вдоль вертикали вниз. Определить коэффициент f трения между поверхностями груза и стола, если массы каждого груза и масса блока одинаковы и грузы движутся с ускорением а = 5,6м 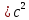 . Проскальзыванием нити по блоку и силой трения, действующей на блок, пренебречь. . Проскальзыванием нити по блоку и силой трения, действующей на блок, пренебречь.Дано: 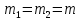 ; ; 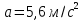 СИ:  Найти:  Решение. 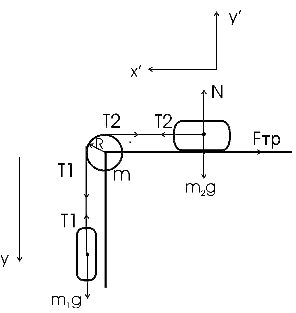 Для первого тела применяем второй закон Ньютона:  где 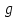 -ускорение свободного падения, -ускорение свободного падения, 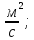 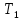 - сила натяжения нити, H. - сила натяжения нити, H.Теперь применим второй закон Ньютона ко второму телу:  Разложим вектора для каждого тела на проекции вдоль оси 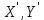 и и  : :проекция на ось  : : 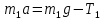 (1) (1)проекция на ось  : : 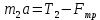 (2) (2)проекция на ось 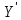 : :  (3) (3)Также запишем второй закон Ньютона для блока: 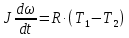 (4) (4)где 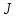 - момент инерции блока, - момент инерции блока,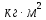 . .Известно, что для однородного диска массой 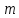 и радиусом и радиусом  момент инерции: момент инерции: Если проскальзывания нити по блоку нет, то: 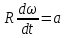 где 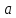 – ускорение грузов, – ускорение грузов, 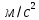 , , - угловое ускорение блока, - угловое ускорение блока, 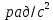 . .тогда 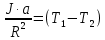 то  сила трения по определению равна 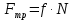 , ,поэтому 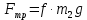 . .Подставляем в (2) 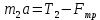 : :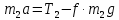 . .Теперь сложим с (1): 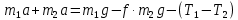 . .Подставим 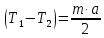 : :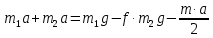 , ,откуда 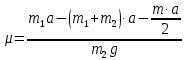 . .Из условий задачи известно, что 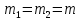 , поэтому , поэтому Проверим размерности расчетных формул 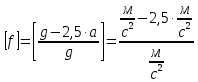 Подставляя числовые значения получим ответ  ед. ед.Ответ: 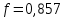 ед ед1.59. Горизонтальная платформа массой  = 150 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой = 150 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой  .Человек массой .Человек массой 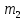 = 70 кг стоит при этом на краю платформы. С какой угловой скоростью = 70 кг стоит при этом на краю платформы. С какой угловой скоростью  начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу круглым, однородным диском, а человека - материальной точкой. начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу круглым, однородным диском, а человека - материальной точкой.Дано:  СИ: 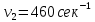 Найти:  Решение. 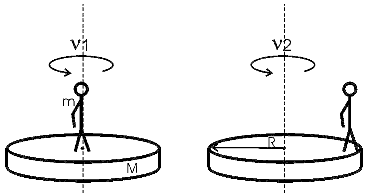 Найдем частоту вращения диска с человеком 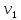 , когда человек перешел в центр диска. Для этого воспользуемся законом сохранения момента импульса: , когда человек перешел в центр диска. Для этого воспользуемся законом сохранения момента импульса: где 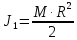 – момент инерции сплошного диска радиусом – момент инерции сплошного диска радиусом  и массой и массой  , , 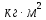 ; ; - начальная частота вращения человека с диском - начальная частота вращения человека с диском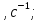  - суммарный момент инерции диска и человека, находящегося на краю диска, - суммарный момент инерции диска и человека, находящегося на краю диска, 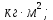 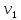 - частота вращения после перехода человека в центр, - частота вращения после перехода человека в центр,  Момент инерции человека 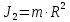 , так как он стоял на расстоянии , так как он стоял на расстоянии  от оси вращения. Поэтому от оси вращения. Поэтому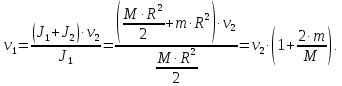 Угловая скорость по определению равна  поэтому поэтому . .Проверим размерности расчетных формул 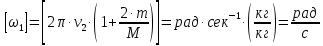 Подставляя числовые значения получим ответ  Ответ:  1.69. Какова масса Земли, если известно, что Луна в течение года совершает 13 обращений вокруг Земли и расстояние от Земли до Луны равно 3,84- 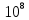 м? м?Дано: 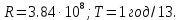 СИ: 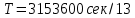 Найти:  Р  ешение. ешение. На всякое тело, движущееся по круговой орбите, действует центростремительная сила (если мы поместим начало координат на теле): 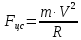 где 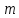 – масса Луны; – масса Луны; – радиус кривизны траектории. – радиус кривизны траектории.Помимо этой силы инерции на тело действует сила всемирного тяготения со стороны Земли: 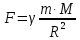 где 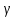 – гравитационная постоянная ( – гравитационная постоянная (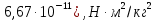 ; ; – масса Земли, кг. – масса Земли, кг.Из третьего закона Ньютона:  откуда 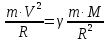 Поэтому скорость Луны  C другой стороны скорость Луны 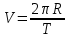 где 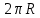 – периметр орбиты, м; – периметр орбиты, м; – период обращения Луны (за 1 год 13 раз), сек. – период обращения Луны (за 1 год 13 раз), сек.Поэтому  Откуда масса Земли 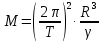 Проверим размерности расчетных формул 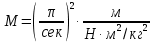 Подставляя числовые значения получим ответ 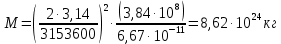 Ответ: 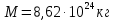 1.79. На гладком горизонтальном столе лежит шар массой 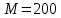 г, прикрепленный к горизонтально расположенной легкой пружине с жесткостью г, прикрепленный к горизонтально расположенной легкой пружине с жесткостью 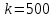 Н/м. В шар попадает пуля массой Н/м. В шар попадает пуля массой  г, летящая со скоростью г, летящая со скоростью 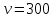 м/с, и застревает в нем. Пренебрегая перемещением шара во время удара и сопротивлением воздуха, определить амплитуду м/с, и застревает в нем. Пренебрегая перемещением шара во время удара и сопротивлением воздуха, определить амплитуду колебаний шара. колебаний шара.Дано:  Н/м Н/м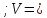 300м/с 300м/с СИ:  Найти:  Решение. 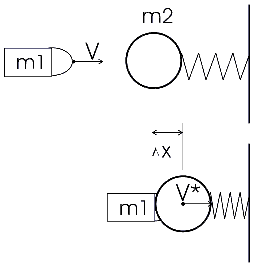 Используем закон сохранения импульса, учитывая, что после удара пуля вошла в шар и их масса стала  : : , ,откуда 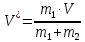 Кинетическая энергия шара и пули после удара:  Подставим эту скорость 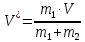 в кинетическую энергию: в кинетическую энергию: Эта энергия идет на деформацию пружины. Энергия деформированной пружины: 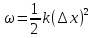 Вся кинетическая энергия переходит в потенциальную при  , тогда , тогда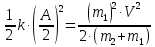 Откуда искомая величина  Проверим размерности расчетных формул 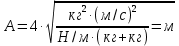 Подставляя числовые значения получим ответ 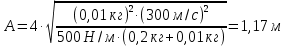 Средняя скорость за четверть периода 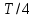 (замедление от максимальной скорости (замедление от максимальной скорости 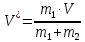 , до нулевой) равна: , до нулевой) равна: 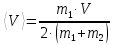 За это время тело сместится на половину амплитуды и поэтому средняя скорость равна: 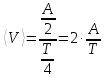 Откуда период равен: 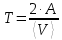 Подставим амплитуду и среднюю скорость:  Проверим размерности расчетных формул 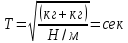 Подставляя числовые значения получим ответ  Ответ:  |
