основы моделирования. детерм задачи. Булайчик. Исследование объектов познания на их
 Скачать 48.43 Kb. Скачать 48.43 Kb.
|
|
Модели́рование — исследование объектов познания на их моделях; построение и изучение моделей реально существующих объектов, процессов или явлений с целью получения объяснений этих явлений, а также для предсказания явлений, интересующих исследователя. МЕТОД МОДЕЛИРОВАНИЯ создание идеальной с точки зрения научных данных модели организации и условий функционирования педагогического процесса или какой-либо его части. Моделирование возможно в процессе изучения и экспериментирования отдельных частных педагогических форм, методов работы, их взаимосвязи между собой; в организации крупномасштабных исследований. Метод моделирования применяется при разработке учебного плана, организации учебного или производительного труда, программы воспитания и режима. Моде́ль (фр. modèle, от лат. modulus — «мера, аналог, образец») — это упрощенное представление реального устройства и/или протекающих в нем процессов, явлений. Математи́ческая моде́ль — это математическое представление реальности[1]. При построении моделей объектов используется системный подход (Под системой понимают группу взаимосвязанных элементов, действующих совместно с целью выполнения заранее поставленной задачи), представляющий собой методологию решения сложных задач, в основе которой лежит рассмотрение объекта как системы, функционирующей в некоторой среде. Функциональный подход в моделировании бизнес-процессов сводится к построению схемы бизнес-процесса в виде последовательности бизнес-функций, с которыми связаны материальные и информационные объекты, используемые ресурсы, организационные единицы и т. п. Преимуществом функционального подхода является наглядность последовательности и логики операций в бизнес-процессах компании, а недостатком — некоторая субъективность в детализации операций. Процесс создания математической модели условно можно разбить на ряд основных этапов: 1) построение математической модели; 2) постановка, исследование и решение соответствующих вычислительных задач; 3) проверка качества модели на практике и модификация модели. Принципы построения математических моделей Рассмотрим основные принципы моделирования, отражающие опыт, накопленный к настоящему времени в области разработки и использования ММ. 1. Принцип информационной достаточности. При полном отсутствии информации об исследуемой системе построение её модели невозможно. При наличии полной информации о системе её моделирование лишено смысла. Существует некоторый критический уровень априорных сведений о системе (уровень информационной достаточности), при достижении которого может быть построена её адекватная модель. 2. Принцип осуществимости. Создаваемая модель должна обеспечивать достижение поставленной цели исследования с вероятностью, существенно отличающейся от нуля, и за конечное время. 3. Принцип множественности моделей. Данный принцип является ключевым. Речь идёт о том, что создаваемая модель должна отражать в первую очередь те свойства реальной системы (или явления), которые влияют на выбранный показатель эффективности. Соответственно при использовании любой конкретной модели познаются лишь некоторые стороны реальности. Для более полного её исследования необходим ряд моделей, позволяющих с разных сторон и с разной степенью детальности отражать рассматриваемый процесс. 4. Принцип агрегирования. В большинстве случаев сложную систему можно представить состоящей из агрегатов (подсистем), для адекватного математического описания которых оказываются пригодными некоторые стандартные математические схемы. Принцип агрегирования позволяет, кроме того, достаточно гибко перестраивать модель в зависимости от задач исследования. 5. Принцип параметризации. В ряде случаев моделируемая система имеет в своём составе некоторые относительно изолированные подсистемы, характеризующиеся определённым параметром, в том числе векторным. Такие подсистемы можно заменять в модели соответствующими числовыми величинами, а не описывать процесс их функционирования. При необходимости зависимость значений этих величин от ситуации может задаваться в виде таблицы, графика или аналитического выражения (формулы). Принцип параметризации позволяет сократить объем и продолжительность моделирования. Однако надо иметь в виду, что параметризация снижает адекватность модели. Виды математических моделей В зависимости от того, какими средствами, при каких условиях и по отношению к каким объектам познания реализуется способность моделей отображать действительность, возникает их большое разнообразие, а вместе с ним — классификации. Путем обобщения существующих классификаций выделим базовые модели по применяемому математическому аппарату, на основе которых получают развитие специальные модели (рисунок 8.1). 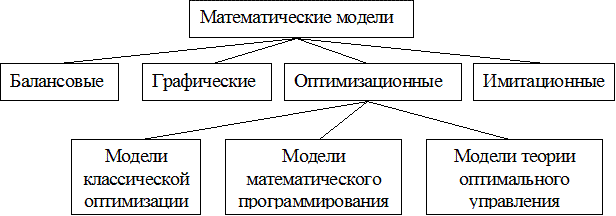 Рисунок 8.1 - Формальная классификация моделей |
