РГЗ_УИ. Исследование процесса развития техники и технологий
 Скачать 425.77 Kb. Скачать 425.77 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Комсомольский-на-Амуре государственный университет» Электротехнический факультет Кафедра ЭПАПУ РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ по дисциплине «Управление инновациями» Исследование процесса развития техники и технологий
В качестве исследуемого объекта выступаю отечественные дозвуковые реактивные самолеты-истребители. Основным показателем, характеризующие уровень параметров технологии и качества продукции, выступает развиваемая тяга. Исходные данные представлены в таблице 1. Таблица – Основные тактико-технические характеристики отечественных дозвуковых реактивных самолетов-истребителей
Продолжение таблицы 1
Построение характеристики будет осуществляться в виде следующей функции:  (1) (1)где А – коэффициент, увеличивающий (уменьшающий) масштаб S-образной кривой; B – коэффициент, характеризующий точку перегиба кривой; C – коэффициент сдвига кривой по оси Y. Первоначально произвели ввод данных в системе Microsoft Office Excel согласно варианту задания, данный этап показан на рисунке 1.  Рисунок – Ввод данных для расчета (частично) Далее было выполнено построение точечной диаграммы по имеющимся данным. Диаграмма представлена на рисунке 2. Рисунок – Точечная диаграмма Затем выполнили расчет линии регрессии с помощью уравнения (1). Первоначально используемые коэффициенты были выбраны произвольно. Результаты расчета представлены в таблице 2. Иллюстрация этапа представлена на рисунке 3. 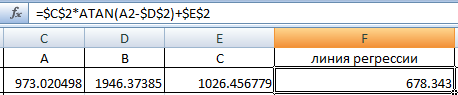 Рисунок – Расчет линии регрессии Для того чтобы воспользоваться функцией Поиск решения для построения линии регрессии, наиболее приближенной к наилучшей теоретической функции и дальнейшего расчета «критерия согласия», необходимо найти целевую ячейку (рисунок 4), в которой будет рассчитана сумма «квадрата разности» экспериментальных и теоретических значений функции (линии регрессии).  Рисунок – Определение целевой ячейки Далее для построения линии регрессии необходимо воспользоваться пакетом системы MS Excel Поиск решения (рисунок 5).  Рисунок – Окно надстроек Заполняем все поля согласно варианту задания (рисунок 6).  Рисунок – Поиск решения После сохранения результатов найденного системой MS Excel решения по определению неизвестных коэффициентов А, В, С первоначальные значения в ячейках, соответствующих этим коэффициентам, изменятся автоматически (рисунок 7). 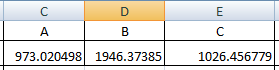 Рисунок – Найденные коэффициенты Далее необходимо построить полученный тренд изменения тяги самолетов в имеющейся диаграмме (рисунок 8). Рисунок – Линия регрессии Основные расчеты выполнены в системе Microsoft Office Excel (таблица 2). Окончательный результат представлен на рисунке 9. Таблица – Расчет S-образной кривой
Продолжение таблицы 2
 Рисунок – S-образная характеристика развития отечественных дозвуковых реактивных самолетов-истребителей Полученные коэффициенты:   
Задание выполняется в системе MatLab. В качестве исходной используем данные из предыдущего задания. Введем два массива данных, на рисунке 10, где x – дата первого полета, а y – значение функции арктангенса.  Рисунок – Введенные массивы данных Далее создаем в системе MATLAB обобщенно-регрессионную сеть GRNN. Ее синтаксис выглядит следующим образом: net = newgrnn(P , T, spread), где P – задание матрицы входных данных; T – задание матрицы цели; spread – задание смещения (отклонения), по умолчанию равен 1. В нашем случае примем величину смещения 0.5. Задаем имя нейронной сети, запрашиваемой в системе MATLAB, например, в виде обозначения b. Результат представлен на рисунке 11.  Рисунок – Результат применения обобщенно-регрессионной сети GRNN Полученные промежуточные точки представлены в таблице 3. Таблица – Промежуточные точки
Для проверки отметим полученные точки на диаграмме (рисунок 12). Рисунок – Промежуточные точки Обобщенная диаграмма представлена на рисунке 13.  Рисунок – Обобщенная диаграмма Определим критерий сходимости:  где  – зависимая переменная уравнения функции арктангенса; – зависимая переменная уравнения функции арктангенса; – среднее значение зависимой переменной; – среднее значение зависимой переменной;y – табличные значения исходных данных.  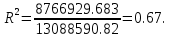 Процедура расчет выполнена в Microsoft Office Excel, представлена на рисунке 14. 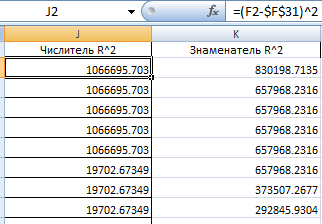 Рисунок – Расчет критерия сходимости Полученный критерий сходимости показывает, насколько точно линия регрессия описывает имеющиеся данные. В нашем случае, точность полученной регрессии не высока из-за существенного разброса точек.
S-образная кривая по тангенци альной функции:  где А – коэффициент, увеличивающий (уменьшающий) масштаб S-образной кривой; B – коэффициент, характеризующий точку перегиба кривой; C – коэффициент сдвига кривой по оси Y.   S-образная кривая Перла:  где L – верхний предел переменной. 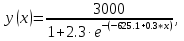  Несимметричная S-образная кривая Гомпертца  где x0 – момент времени, когда относительное замещение достигает своего среднего значения.   S-образная кривая А.Ф. Каменева   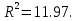 S-образная кривая Фишера-Прая  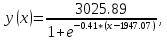  Из всего многообразия регрессионных зависимостей сиг моидального типа (логистическая, гиперболический тангенс, арк тангенс, двойная логистическая функция, логистическая функция в виде решения простого нелинейного дифференциального урав нения первого порядка) наиболее предпочтительной для случая анализа технического уровня изделий (техники, продуктовых ин новаций) является функция арктангенса, а для случая анализа закона диффузии технологий - логистическая функция. Для случая анализа закономерностей диффузии технологий, широкое применение находят логистические закономерности (рисунок 15). Вместе с тем анализ возможностей применения логистиче ских зависимостей для аппроксимации поля эмпирических точек, построенных по параметрам технического уровня изделий, на пример, тяги газотурбинного двигателя, показы вает, что кривые Перла, Гомпертца, Каменева, Фишера-Прая яв ляются менее предпочтительными, чем сигмоиды типа arctg. В этой связи логистические зависимости более целесообразно рассматривать для системного анализа закономерностей диффу зии (распространения) технологий. 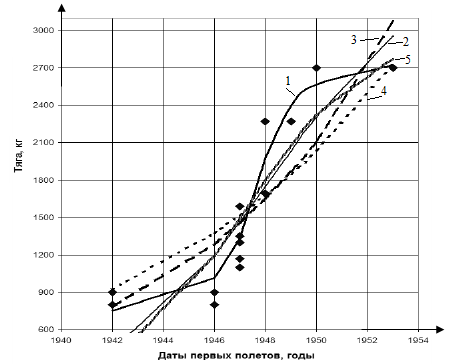 1 – закономерность по тангенциальной функции; 2 – Кривая по зависимости Перла; 3 – закономерность по Гомпертцу; 4 – кривая по функции А.Ф. Каменева; 5 – закономерность по Фишеру-Праю Рисунок – Сопоставительный анализ сигмоид (S-образных кривых) на примере двигателей дозвуковых самолетов-истребителей
Доминирующим фактором современного этапа развития промышленного производства являются технологические сдвиги, т.е. переходы к технике или технологии нового поколения путем разработки «критических технологий», которые позволяют перейти на новые 5-образные (сигмоидальные) кривые развития. Одним из основных научных законов инноватики является закон смены поколений техники и технологий, т. е. изменения принципа действия (выполнения) технологической, энерге тической и информационно-управляющей функции данного поколения техники или технологии для обеспечения роста их конкурентоспособности. Он гласит: «Для обеспечения долговечности и/или конкурентоспособности технических систем их поколения заменяют путем принципиального изменения технологий данной генерации систем». На любой S-образной (сигмоидальной) кривой развития технической системы можно выделить пять участков (периодов), каждый из которых характеризует ту или иную стадию развития поколения самолетов-истребителей. На первом участке происходит зарождение 5-образной кривой. Второй участок – это период интенсивного развития авиационной техники, характеризующийся быстрым ростом тактико-технических характеристик изделий. Эта стадия развития завершается при достижении точки перегиба S-образной кривой развития. На третьем участке S-образной кривой после названной точки перегиба происходит этап дефлирующего развития рассматриваемой авиационной техники. Эта стадия характеризуется падением темпов роста главного параметра технического уровня в данном случае при появлении новых моделей самолетов-истребителей. Четвертый участок кривой – стадия перехода к застою развития техники анализируемого назначения. На данной стадии происходит малосущественное улучшение тактико-технических характеристик (параметров технического уровня и качества изделия). Принцип действия такой техники себя исчерпывает, а сами изделия рассматриваемого типа начинают переходить в стадию морального старения. Пятый участок S-образной кривой – стадия застоя в развитии анализируемой техники. На этой стадии, как правило, не происходит коренного улучшения параметров технического уровня или повышения качества изготавливаемой техники. Объяснение закона смены поколений техники и технологий основывается на описании отличий нескольких волн развития (смежных S-образных кривых). Точки пересечения смежных S-образных кривых в границах технологий применения (назначения) техники называют «критическими точками». При этом следует иметь в виду, что «кризис» – это не фатальное деструктивное явление, приводящее к разрушению старой технологии. Дословный перевод термина «кризис» означает только то, что изменение принципиальной основы техноло гического способа (метода) позволяет решительно перейти к новой, более конкурентоспособной технологии, которая при ходит на смену стареющей технологии того же назначения. Анализ «критических точек», «точек перегиба» и точек перехода к «застою» в развитии техники позволяет определить основные направления инновационной деятельности на каждом из рассматриваемых этапов развития. Знание рассмотренных закономерностей позволяет заранее принять профилактические меры во избежание фатального перехода технической системы к стадиям ее деградации и гибели. Такие ситуации нередко наблюдаются на практике, если разработчики новой техники и технологии упрямо придерживаются в своих действиях только решения задачи эволюционного развития технологической системы даже в условиях перехода технологии в стадию застоя. При этом важно иметь в виду, что в инноватике такие мероприятия по улучшению или обновлению серийно производимой продукции (изделий) в фазе ее зрелости называют квазиинновациями. Из анализа приведенных S-образных кривых смены поколений авиационной техники можно сделать выводы о необходимости выполнения НИОКР для разработки принципиально новых конструкций авиационной техники рассматриваемого назначения, так как научно-технический потенциал существующих технологий совершенствования исчерпан. Такие исследования в значительной степени уже выполнены. Сказанное подтверждает новое поколение гипер звуковых беспилотных самолетов и соответствующих им двигателей. Самолеты новейших технологий должны летать на гиперзвуковых скоростях, а для этого в их двигателях необходимо гармонично объединить черты авиационной и космической техники. 2019 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
