приложения к курсовой. Измерение информации (алфавитный и содержательный подходы)
 Скачать 0.9 Mb. Скачать 0.9 Mb.
|
Приложения 1. Тестовая часть КИМ по теме «Измерение информации (алфавитный и содержательный подходы)»Базовый вариант 1. Сколько байтов составляет сообщение, содержащее 3544 бит? 217; 443; 512; 256; Решение: самостоятельно. 2. Полученное сообщение – «Ваш друг живёт на третьем этаже» содержит 3 бита информации. Сколько в доме этажей? 3; 5; 16; 8. Решение: N = 23 = 8 этажей. Пояснение: информация л каждом из этажей несёт в себе 3 бита, события равновероятны, используя формулу получим количество этажей. Ответ: в доме 8 этажей. 3. Сообщение «Василий проживает в доме №7 на улице Гагарина» содержит 4 бита информации. Найдите количество домов на улице Гагарина. 7; 8; 16; 32; Решение: самостоятельно. Ответ: на улице 16 домов. 4. Две лотереи проводятся по следующей схеме – «пять из шестидесяти четырёх и шесть из сто двадцати восьми. В какой из лотерей сообщение о выигрыше несет большее количество информации? «5 из 64»; «6 из 128»; невозможно вычислить; информации одинаково; Решение: Сообщении о выигрыше в каждой из лотерей содержит одно равновероятное событие из N возможных. Количество информации, в сообщении, находится по формуле Хартли (показательное уравнение): 2i = N, с учётом того, что выпавший шар при розыгрыше лотереи выбирается из 64, затем из 63, 62 и т.д., шаров для первой и из 128, 127 и т.д., шаров для второй. Применяя формулу для каждого случая, получим, для первой лотереи, в общем случае: 2i = 64, 2i = 63, и т.д., для второй лотереи 2i = 128, 2i = 127 и т.д. Находя значения i, для первой лотереиполучим 6, 5,97728 и т.д., для второй 7, 6,98868 и т.д. Суммируя полученные значения для 5 исходов в первой лотереи и для 6 исходов во второй, округляя получим 29,8 и 41,8 соответственно. Сравнивая полученные суммы найдём ответ. Ответ: больше информации несет сообщение о результатах второй лотереи. 5. Сообщение «Ваш друг живет на 10 этаже», содержит 5 бит информации. Сколько в доме этажей? 10; 32; 16; 64. Решение: N = 25 = 32 этажей. Пояснение: события равновероятны, т.к. номера этажей уникальны. Ответ: в доме 32 этажа. 6. Определите количество информации в битах которое получил игрок №2 после первого хода игрока №1 в игре «Крестики-нолики», учитывая, что размер поля равен 4 х 4? Решение: Пусть игрок №1 поставил в клетку поля крестик, учитывая, что игрок может его поставить в любую из 16 клеток (n) найдём количество информации i используя формулу Хартли: n = 2i, 16=2i, 24=2i, i= 4. Ответ: количество информации, полученное игроком №2 равно 4 бита. 7. Сообщение о том, что интересующая Вас книга находится на 7 полке, несет 4 бита информации. Сколько полок на книжном стеллаже? 10 8 16 12 Решение: самостоятельно. 8. Выберите утверждение которое не является информацией согласно теории Шеннона. Компьютер - устройство для обработки с информации Бла-бла-бла Температура воздуха +30  «Волга» - река Решение: самостоятельно. 9. Какое количество вопросов необходимо для угадывания числа N принадлежащего множеству N 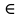 [1,32]? [1,32]?5 3 4 7 Решение: самостоятельно. 10. Найдите количество вагонов в поезде по тексту «Приеду вагоне номер 5», если известно, что сообщение несёт 4 бита информации. 16 4 64 информации недостаточно Решение: самостоятельно. 11. Полученное сообщение размером 82 символа состоит из алфавита мощностью 16-символов. Найдите объем информации в сообщении. В ответе запишите найденный объём в битах. Решение: Мощность алфавита N = 16 Сообщение содержит 82 символа Вес одного символа 16 = 2b, равен (b = 4) бита Объем информации 82×4 = 328 бита Ответ: объем информации 328 бита. 12. Объём сообщения, содержащего 256 символов равен 0,125 Кбайт. Найдите мощность используемого алфавита. Решение: 1. Вес сообщения 0,125 х 210 х 8 = 1024 бита; 2. Вес одного символа N = 1024 / 256 = 4 бита; 3. Символов в алфавите 24 = 16 символов. Ответ: мощность используемого алфавита равна 16 символов. Расширенный вариант Включает все задания базового уровня и следующие дополнительные задания: 1. Определите количество информации в битах если известно, что оно уменьшает неопределенность знания об исходе произвольного события ровно в два раза. 1; 2; 3; 4; Решение: самостоятельно. 2. На вопрос: «Вы выходите на следующей остановке?», получен ответ: «нет». Определите количество информации, содержащейся в ответе на поставленный вопрос. Решение: количество исходов события (ответ на вопрос) «Да» или «Нет» равно двум (N = 2). Используя формулу N = 2iнайдем i(2 = 2i), i = 1 бит. Ответ: количество информации, содержащейся в ответе равно 1 биту. 3. На вопрос: «Петя! Ты пойдешь сегодня в кино?», получен ответ: «да». Определите количество информации, содержащейся в ответе на поставленный вопрос. Решение: самостоятельно 4. Светофор сменил цвет с жёлтого на зелёный. Определите количество информации полученной наблюдателем за данным процессом? Решение: самостоятельно Ответ: 1 бит. 5. После жеребьёвки спортсмену выпало плыть по дорожке №4, определите количество информации, полученной спортсменом, если известно, что всего дорожек 4. Решение: из 4 дорожек необходимо выбрать одну, т.е. N = 4. Дальнейшее решение проведите самостоятельно, учитывая, что выбор дорожки есть равновероятное событие. Ответ: 2 бита. 6. Из коробки, содержащей 16 кубиков разных цветов вынули кубик. Определите количество информации, полученной вынувшим красный кубик. Решение: Все 16 событий (выемка кубика) равновероятны. Необходимо выбрать одно из 16 событий. Проведите дальнейшее решение самостоятельно. Ответ: 4 бита. 7. За курс обучения учащийся получил 52 различные оценки. Определите количество оценок «5», если количество информации о получении одной оценки «5» равно 2 битам. (оценки 0 и 1 не существует) Дано: N = 52, i4 = 2 бита. Решение: Проведите решение самостоятельно используя формулу Шеннона по следующей схеме: 1) i4 = (решение) = 1/4 – вероятность получения «5»; 2) K4 = (решение) = 13 – количество «5». Ответ: 13 пятерок. 8. Белую, синюю и коричневую краски использовали при проведении ремонтных работ. Известно, что количество использованных банок белой и синей краски одинаково. Сообщение «закончилась краска белого цвета», несет 2 бита информации. Определите израсходованное количество банок коричневой краски, учитывая, что расход синей краски составил 8 банок. Дано: 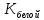 = = 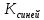 = 8, i6елой = 2 бита. = 8, i6елой = 2 бита.Найти: 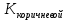 Решение:  1.Найдём вероятность расхода одной банки белой краски;  2.Найдем исходное количество банок с белой краской; 3. 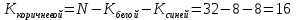 – банок коричневой краски. – банок коричневой краски.Самостоятельно: поясните решение задачи. Ответ: 16 банок коричневой краски. 9. В корзине лежат шары двух цветов. Среди них 18 шаров одинакового цвета. Определите количество шаров, учитывая, что информация «Из корзины достали шар одно цвета», содержит 2 бита информации. (Задача повышенной трудности. Упрощение: представьте, что в корзине лежат шары белого и черного цветов). Дано: К = 16, i = 2 бита. Найти: N. Решение: 1) 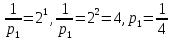 – вероятность извлечения шара одного цвета; – вероятность извлечения шара одного цвета;2)  где  = 6 шаров одного цвета. = 6 шаров одного цвета.3) 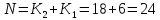 шара было в корзине. шара было в корзине.Самостоятельно: поясните решение задачи. Ответ: в корзине лежало 24 шара. 11. мощность первого алфавита равна 32, второго - 64. Сообщение, составленное с помощью первого алфавита, содержит 80 символов. Сообщение, составленное с помощью второго алфавита, содержит 70 символов. Найдите какое из сообщений имеет наибольший информационный объём. в первом сообщении объем информации меньше, чем во втором; одинаково; во втором сообщении объем информации меньше, чем в первом. Решение: самостоятельно. Приложение 2. Презентационная частьПрезентация на тему «Измерение информации содержит 30 слайдов». В приложении приведены примеры нескольких слайдов. С  лайд №1. Единицы измерения информации С  лайд №2. Как измерить информацию С  лайд №27. Практикум С  лайд № 31. Домашнее задание |
