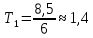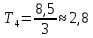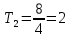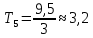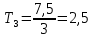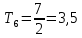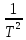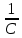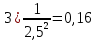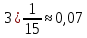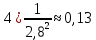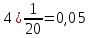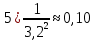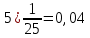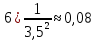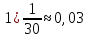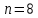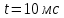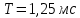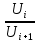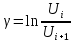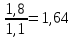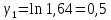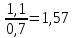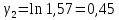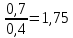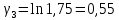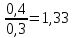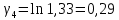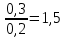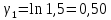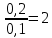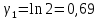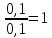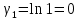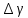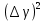Главная страница
Навигация по странице:

  • Принадлежности

  • Порядок выполнения работы

  • График зависимости 1/ Т

  • Результаты измерений и расчётов занесены в таблицу 1

  • Результаты измерений и расчётов занесены в таблицу 2

    		•

    лабораторная по физике нна тему ИЗУЧЕНИЕ СОБСТВЕННЫХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ В КОНТУРЕ. Отчёт по лабораторной работе. изучение собственных электромагнитных колебаний в контуре


    Скачать 47.9 Kb.
    Названиеизучение собственных электромагнитных колебаний в контуре
    Анкор лабораторная по физике нна тему ИЗУЧЕНИЕ СОБСТВЕННЫХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ В КОНТУРЕ
    Дата15.06.2021
    Размер47.9 Kb.
    Формат файлаdocx
    Имя файлаОтчёт по лабораторной работе.docx
    ТипИсследование
    #217791



    ОТЧЁТ ПО ЛАБОРАТОРНОЙ РАБОТЕ

    НА ТЕМУ: «ИЗУЧЕНИЕ СОБСТВЕННЫХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ В КОНТУРЕ»
    Цель работы:

    1. Познакомиться с характером собственных затухающих электромагнитных колебаний в контуре.

    2. Исследовать зависимость периода колебаний от ёмкости конденсатора и определить индуктивность катушки в контуре.

    3. Определить логарифмический декремент затухания.

    Принадлежности: колебательный контур, источник постоянного тока, вольтметр, осциллограф, компьютер.
    Порядок выполнения работы:
    Упражнение 1. Исследование зависимости периода колебаний в колебательном контуре от емкости конденсатора и определение индуктивности катушки.

    1. Установите сопротивление резистора R, соответствующее номеру вашего вариан- та* (таблица 3), а электроемкость конденсатора C = 5 мкФ.

    Вариант №7

    R, Ом
    7

    C, мкФ
    4




    1. Включите источник питания и переключите ключ К в положение 2. В контуре возникнут электромагнитные колебания и на экране будет выводится зависимость напряжения на обкладках конденсатора от времени U(t).

    2. Определите полное число колебаний n, которые поместились на экране и время этих колебаний t. Определите период колебаний Т по формуле T = t / n . Занесите результаты в таблицу 1.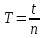












    1. Переключите ключ К в положение 1, в результате произойдет новая зарядка конденсатора.

    2. Увеличивая ёмкость конденсатора каждый раз на 5 мкФ повторите пп. 2–4 еще 5 раз при различных значениях С.

    3. Для каждого случая рассчитайте величину, обратную квадрату периода колебаний 1/Т2 и величину, обратную электроемкости 1/С. На миллиметровой бумаге постройте график зависимости 1/Т2 = f(1/С). Сделайте вывод о характере зависимости.


























    График зависимости 1/Т2 = f(1/С):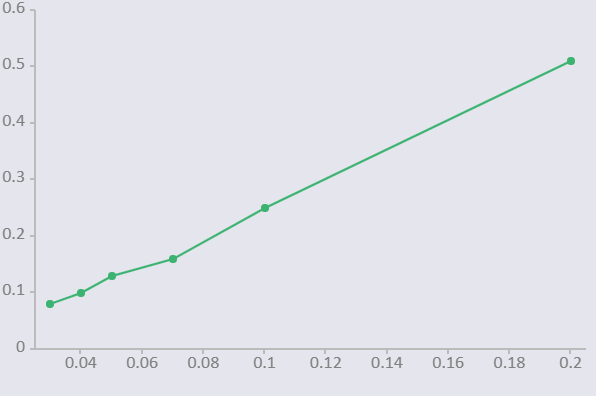



    Вывод:

    Мы рассчитали величину обратную квадрату периода колебаний (1/Т2) и величину обратную электроёмкости (1/С), затем на основе полученных данных построили график зависимости 1/Т2 = f(1/С). Из данного графика видно, что полученная зависимость носит линейный характер, что согласуется с теорией.

    Результаты измерений и расчётов занесены в таблицу 1:


    №
    R, Ом
    С,

    мкФ
    n
    t, мс
    T, мс
    1/Т2, мс-2
    1/C, мкФ-1

    1


    7
    5
    6
    8,5
    1,4
    0,51
    0,2

    2
    10
    4
    8,0
    2,0
    0,25
    0,1

    3
    15
    3
    7,5
    2,5
    0,16
    0,07

    4
    20
    3
    8,5
    2,8
    0,13
    0,05

    5
    25
    3
    9,5
    3,2
    0,10
    0,04

    6
    30
    2
    7,0
    3,5
    0,08
    0,03



    1. По графику рассчитайте индуктивность контура L. Из уравнения (7) следует, что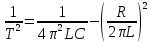



    Поэтому тангенс угла наклона прямой линии на графике зависимости 1/Т2 от 1/Ссвязан с индуктивностью Lсоотношением: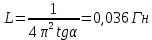



    1. Полученное значение L немного не сходится c номинальным значением индуктивности (L = 0,01 Гн).


    Упражнение 2. Исследование затухания колебаний и определение логарифмического декремента затухания.


    1. Установите сопротивление резистора R и емкости конденсатора C согласно номеру вашего варианта (таблица 3).

    Вариант №7

    R, Ом
    7

    C, мкФ
    4



    1. Создайте в контуре затухающие электромагнитные колебания и получите на экране монитора зависимость напряжения на обкладках конденсатора от времени U(t).

    2. Определите полное число колебаний n, которые поместились на экране и время этих колебаний t. Определите период колебаний Т по формуле T = t / n . Занесите результаты в таблицу 2.






    1. Используя миллиметровую линейку, определите амплитуду всех колебаний U1– Un(см. рис. 4). Рассчитайте отношение последовательных амплитуд Ui/Ui+1, отстающих друг от друга на один период, и определите логарифмический декремент затухания 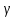для каждой пары амплитуд по формуле (9) и проведите статистическую обработку результатов.






























    Проведём статическую выборку из 7 значений:

    1. Суммируя значения ранжированного вариационного ряда, определяем выборочное среднее: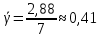



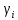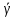    1. В седьмом столбце таблицы 2 запишем разности между каждой составляющей выборки   и выборочным средним   , а в восьмом столбце данной таблицы их квадраты.

    2. Определим коэффициент Стьюдента в зависимости от доверительной вероятности (P=0,95) и количества опытов (n=7):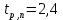



    1. Рассчитаем случайную составляющую абсолютной погрешности: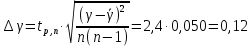



    1. Получим: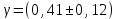



    Результаты измерений и расчётов занесены в таблицу 2:

    №
    R, Ом
    С, мкФ
    Ui, В
    Ui

    Ui+1






    1

    7

    4
    1,8
    1,64
    0,5
    0,09
    0,0081

    2
    1,1
    1,57
    0,45
    0,04
    0,0016

    3
    0,7
    1,75
    0,55
    0,14
    0,0196

    4
    0,4
    1,33
    0,29
    0,12
    0,0144

    5
    0,3
    1,5
    0,40
    0,01
    0,0001

    6
    0,2
    2
    0,69
    0,28
    0,0784

    7
    0,1
    1
    0
    0,41
    0,1681

    8
    0,1
    0
    -
    -
    -

    Ср.






    0,41









    1. Рассчитайте теоретическое значение логарифмического декремента затухания по формуле (10) с учётом сопротивления катушки Rки периода (11):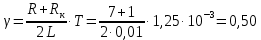




    Вывод:

    Мы рассчитали теоретическое значение логарифмического декремента и оно совпало с величиной 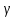, найденной в эксперименте, а это значит, что все расчёты проведены верно.

    написать администратору сайта