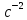Лаба 1. Изучение вращательного движения на маятнике Обербека. Изучение вращательного движения на маятнике Обербека
 Скачать 85.63 Kb. Скачать 85.63 Kb.
|
|
Лабораторная работа. Тема: «Изучение вращательного движения на маятнике Обербека» Цель работы: Экспериментальная проверка уравнения динамики вращательного движения твердого тела. Измерительные приборы: Секундомер Линейка Цена деления линейки: 10 см Цена деления секундомера 0.01 с. Схема установки: 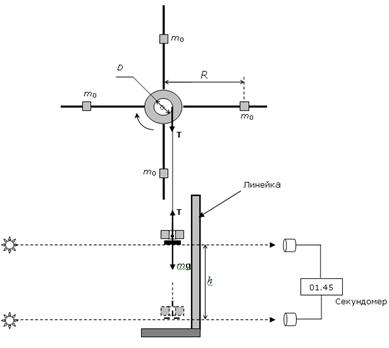 Путь платформы h =1,600 м. Длина стержней от оси вращенияl =0,230 м. Диаметр шкива D=0,020м. Масса платформы 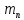 =0,100 кг. =0,100 кг.Масса груза на стержнях 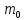 =0,140 кг. =0,140 кг.Масса стержня 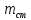 = 0,090 кг. = 0,090 кг.Расстояние от оси вращения до положения грузов 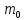 на стержне R= 0,220 м на стержне R= 0,220 мХод работы Таблица. Результаты измерений:
Расчет момента силы натяжения нити: 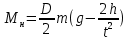 Расчет углового ускорения: 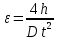 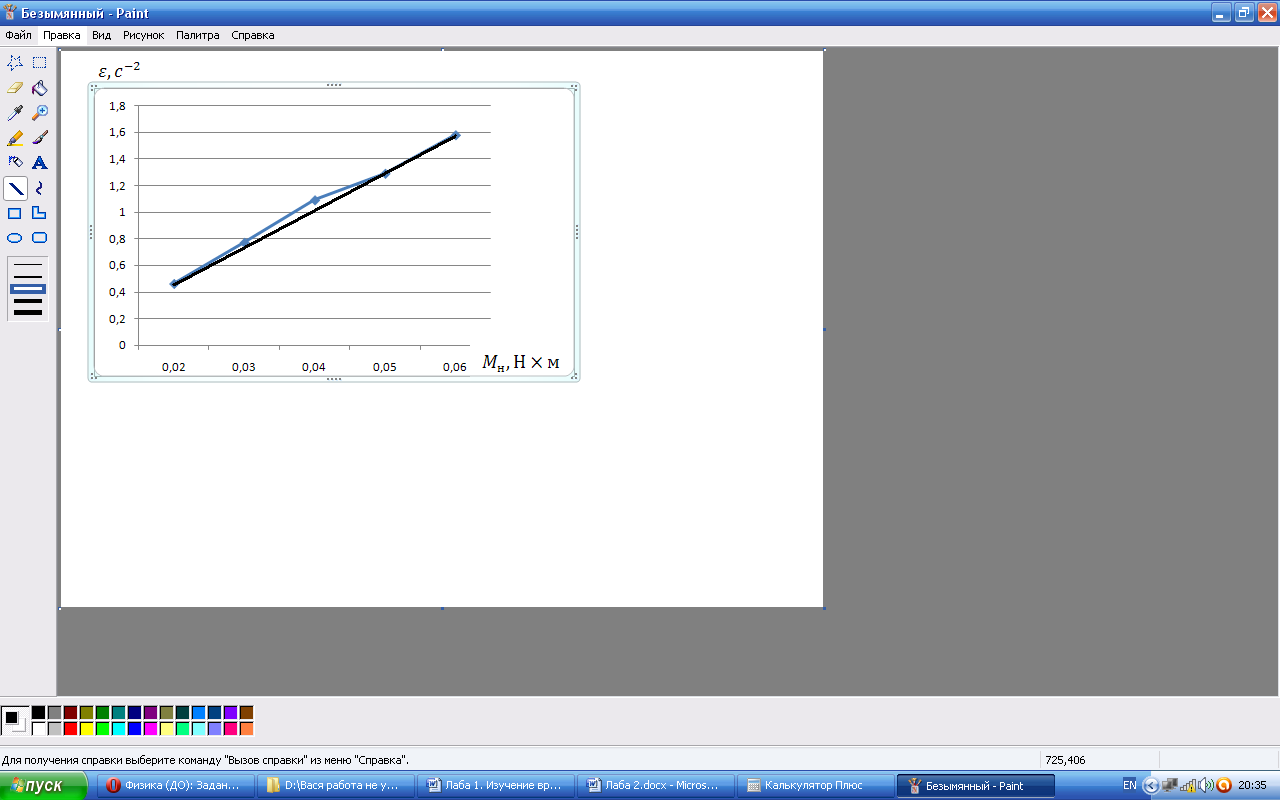 Рис. 1. График зависимости 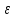 от от 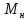 Расчет экспериментального значения момента инерции маятника 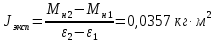 Теоретическое значение момента инерции маятника: 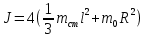 = 0,0334 = 0,0334 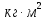 Сравнение теоретического и экспериментального значения момента инерции: 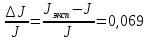 – отличие экспериментального и теоретического значения момента инерции менее чем на 7% дает хорошее согласие теории и опыта. – отличие экспериментального и теоретического значения момента инерции менее чем на 7% дает хорошее согласие теории и опыта. Вывод: В результате проведенного эксперимента получено хорошее согласие экспериментальных данных с данными полученными в результате использования уравнения динамики вращательного движения тела, что говорит о применимости данного уравнения в соответствующих расчетах. Ответы на контрольные вопросы: В эксперименте с маятником Обербека проверяется закон сохранения момента импульса, при этом измеряется время опускания платформы с различным грузом. 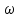 – угловая скорость вращения маятника(направлено на нас) – угловая скорость вращения маятника(направлено на нас)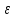 – угловое ускорение маятника(направлено на нас) – угловое ускорение маятника(направлено на нас) – момент силы натяжения нити: – момент силы натяжения нити: 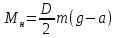 , , , ,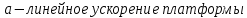 (направлено на нас) (направлено на нас) – момент силы трения качения в оси блока(направлено от нас) – момент силы трения качения в оси блока(направлено от нас)Т.к. 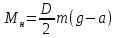 , где a –линейное ускорение: , где a –линейное ускорение: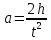 – по формулам кинематики, где t – время опускания платформы, то – по формулам кинематики, где t – время опускания платформы, то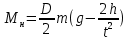 Линейное ускорение связано с угловым следующей формулой: 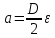 и тогда: и тогда: 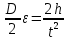 и и 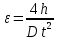 . .Момент инерции системы состоит из моментов инерции четырех масс 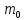 . Момент инерции каждой массы равен: . Момент инерции каждой массы равен: 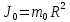 , R – расстояние масс от оси вращения, и момента инерции4-х стержней: , R – расстояние масс от оси вращения, и момента инерции4-х стержней: 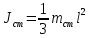 , тогда суммарный момент инерции будет: , тогда суммарный момент инерции будет: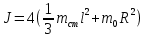 Потому что при увеличении массы перегруза, момент сил трения перестанет быть постоянным и начнет расти вместе с ростом момента силы натяжения нити. Чтобы учесть все силы, действующие на маятник, потому что, если маятник при отсутствии нагрузки начнет двигаться, значит, на него действуют дополнительные, не учтенные силы. Как правило такая ситуация может возникнуть, если расстояния масс 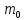 различны и центр масс не совпадает с центром вращения. различны и центр масс не совпадает с центром вращения. |

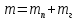
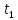 , c
, c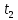 , c
, c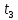 , c
, c