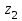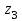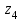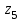Ь3жнвжннв. ПРАКТИЧЕСКАЯ++РАБОТА+№5 (1). Кинематический анализ планетарнозубчатых механизмов
 Скачать 420.89 Kb. Скачать 420.89 Kb.
|
|
1 ПРАКТИЧЕСКАЯ РАБОТА «КИНЕМАТИЧЕСКИЙ АНАЛИЗ ПЛАНЕТАРНО-ЗУБЧАТЫХ МЕХАНИЗМОВ» Цель работы Углубление и закрепление теоретических знаний, развитие умений и практических навыков студентов в области аналитических и графических методов кинематического анализа плоских планетарно-зубчатых механизмов. Определение передаточного отношения и угловой скорости выходного звена многоступенчатых зубчатых передач. Краткие теоретические сведения Зубчатые механизмы – самые распространенные механизмы в металлорежущих станках, транспортных, строительных, горных и дорожных машинах. Простейший зубчатый механизм состоит из двух подвижно соединенных между собой зубчатых колес (рисунок 1.1). Меньшее из двух контактируемых зубчатых колес называется шестерней, а большее – зубчатым колесом. Зубчатые механизмы передают вращение от одного вала к другому, изменяя величины и направления угловой скорости ведомого (выходного) звена. Основной кинематической характеристикой зубчатого механизма является передаточное отношение, определяемое соотношением угловых скоростей, диаметром или чисел зубьев колес 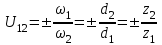 . (1.1) . (1.1)Здесь 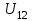 - передаточное отношение от колеса 1 к колесу 2; - передаточное отношение от колеса 1 к колесу 2; 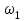 и и 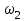 - угловые скорости колеса 1 и колеса 2 соответственно; знак «плюс» или «минус» определяет вид зацепления. Если колеса вращаются в одном направлении, - угловые скорости колеса 1 и колеса 2 соответственно; знак «плюс» или «минус» определяет вид зацепления. Если колеса вращаются в одном направлении, то передаточное отношение положительно (внутреннее зацепление, рисунок 1.1 б), если в разные стороны – отрицательное (внешнее зацепление, рисунок 1.1 а). Простые зубчатые механизмы обеспечивают сравнительно небольшие передаточные отношения. При больших передаточных отношениях применяются сложные многоступенчатые зубчатые передачи. На рисунке 1.2 приведен сложный зубчатый механизм, состоящий из простого зубчатого механизма с колесами 1 и 2 и планетарного механизма с колесами 3, 4, 5, 6 и рычага (водило) Н. 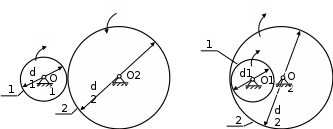 а) б) Рисунок 1.1 – Простые зубчатые механизмы Планетарным называют те зубчатые механизмы, у которых оси некоторых колес (колеса 4 и 5 Рисунок 1.2) перемещаются в пространстве. Передаточное отношение многоступенчатых механизмов, соединенных последовательно, равно произведению их передаточных отношений. Для механизма, показанного на рисунке 1.2, расчетная зависимость имеет вид: 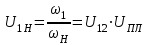 , (1.2) , (1.2)где 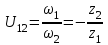 - передаточное отношение простой зубчатой передачи; - передаточное отношение простой зубчатой передачи;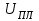 - передаточное отношение планетарного механизма. - передаточное отношение планетарного механизма.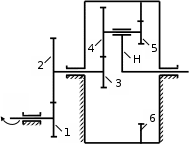 Рисунок 1.2 – Планетарно-зубчатый механизм Связь между угловыми скоростями и числами зубьев колес планетарных механизмов устанавливается с помощью метода мысленной остановки водила Н (Метод Виллиса). Метод основан на положении, что относительное движение звеньев не изменится, если всем звеньям сообщить дополнительное вращение. Исходные данные для расчета Схема планетарно-зубчатого механизма (Рисунок 1.3), модуль m и числа зубьев колес выбираются из таблицы 1.1, в соответствии с номером варианта, закрепленным за студентом. Число зубьев колеса 6 определяется из условия соосности планетарного механизма. Пример расчета Ниже, в качестве примера, выполнен кинематический анализ планетарно-зубчатого механизма, изображенного на рисунке 1.2, при числах зубьев колес 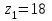 ; ; 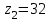 ; ; 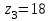 ; ; 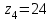 ; ; 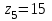 , модуле , модуле 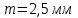 и угловой скорости входного звена и угловой скорости входного звена 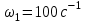 . .1.4.1 А н а л и т и ч е с к и й м е т о д Полагаем, что зубчатые колеса 3, 4, 5 и 6 планетарного механизма вращаются соответственно со скоростями 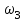 , , 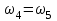 , а колесо 6 неподвижно ( , а колесо 6 неподвижно (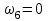 ). Сообщим всем звеньям планетарного механизма дополнительное вращение с угловой скоростью, равной по величине, но противоположной по направлению угловой скорости водила. Тогда звенья механизма будут иметь угловые скорости: ). Сообщим всем звеньям планетарного механизма дополнительное вращение с угловой скоростью, равной по величине, но противоположной по направлению угловой скорости водила. Тогда звенья механизма будут иметь угловые скорости:центральное колесо 3 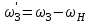 ; ;центральное колесо 6 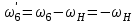 ; ;сателлит 4 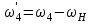 ; ;водило Н 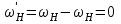 . .Водило остановилось. При этом планетарный механизм превращается в рядовое соединение зубчатых колес (Рисунок 1.4) с передаточным отношением 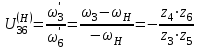 . (1.3) . (1.3)Уравнение (1.3) позволяет определить искомое передаточное отношение планетарного механизма 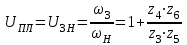 (1.4) (1.4)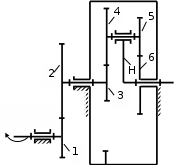 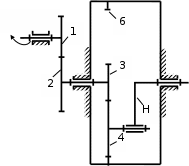 а) б) 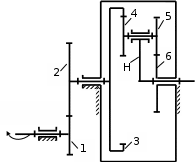 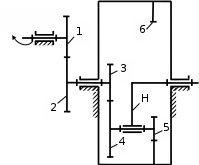 в) г) Рисунок 1.3 – Планетарно-зубчатые механизмы Таблица 1.1 – Варианты исходных данных к работе № 1
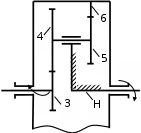 Рисунок 1.4 – Рядовой механизм Число зубьев 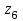 определяется из условия соосности центральных колес планетарного механизма: определяется из условия соосности центральных колес планетарного механизма: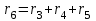 . .Модуль зубчатых колес одинаков, следовательно условие соосности можно записать через числа зубьев 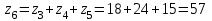 . .Окончательно 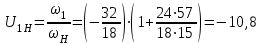 . .Угловая скорость вращения выходного вала (водила) исследуемого зубчатого механизма 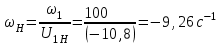 . .Г р а ф и ч е с к и й м е т о д (м е т о д п р о ф. С м и р н о в а Л.) Метод основан на построении треугольников линейных скоростей каждого звена. Графические построения проводят следующим образом. 1.4.2.1 Полагают, что зубчатые колеса нарезаны без смещения инструмента, затем рассчитывают делительные диаметры зубчатых колес по формуле: 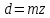 , ,откуда 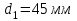 ; ; 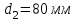 ; ; 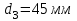 ; ; 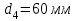 ; ; 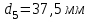 ; ; 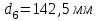 . .1.4.2.2 Строго в масштабе 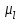 изображают кинематическую схему исследуемого механизма (Рисунок 1.5,а) и обозначают заглавными буквами латинского алфавита кинематические пары на схеме. изображают кинематическую схему исследуемого механизма (Рисунок 1.5,а) и обозначают заглавными буквами латинского алфавита кинематические пары на схеме.1.4.2.3 Проводят вертикаль ху и переносят на вертикаль характерные точки кинематической схемы (точки О1, А, О2, В, К, С). 1.4.2.4 Откладывают отрезок 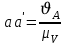 соответствующий вектору скорости точки А колеса соответствующий вектору скорости точки А колеса 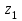 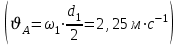 . Масштабным коэффициентом линейных скоростей задаются, например, . Масштабным коэффициентом линейных скоростей задаются, например, 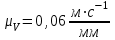 , последний определяет длину отрезка , последний определяет длину отрезка 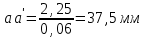 . .Соединяя точки 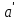 и и 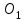 прямой линией (под углом прямой линией (под углом 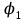 к вертикали), получают треугольник линейных скоростей точек колеса 1. к вертикали), получают треугольник линейных скоростей точек колеса 1.Треугольники линейных скоростей блока из колес 2 и 3 строятся по известным скоростям двух точек: точки А и точки 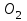 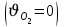 . Прямая . Прямая 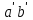 определит закон распределения линейных скоростей точек колес 2 и 3. определит закон распределения линейных скоростей точек колес 2 и 3.1.4.2.5 Треугольник скоростей точек сателлита, состоящего из блока колес 4 и 5, строится по известным скоростям точек В 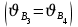 и С ( и С (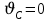 , так как колесо 6 неподвижно). Луч , так как колесо 6 неподвижно). Луч 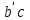 определяет закон распределения линейных скоростей точек, лежащих на сателлите, в том числе и скорость точки К водила. определяет закон распределения линейных скоростей точек, лежащих на сателлите, в том числе и скорость точки К водила.Наконец, луч 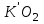 определит закон распределения линейных скоростей точек водила. определит закон распределения линейных скоростей точек водила.Для получения наглядного представления о величине угловых скоростей и направлении вращения всех подвижных звеньев передачи строят пучок лучей с общей точкой S (Рисунок 1.5,в), каждый из которых составляет с вертикалью соответствующий угол 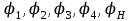 . Так как катеты этих углов пропорциональны угловым скоростям соответствующих звеньев, то точки 1, 2, 3, 4 и h пересечения этих лучей с любой горизонтальной линией Т-Т определяют отрезки . Так как катеты этих углов пропорциональны угловым скоростям соответствующих звеньев, то точки 1, 2, 3, 4 и h пересечения этих лучей с любой горизонтальной линией Т-Т определяют отрезки 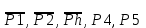 , длина которых пропорциональна угловой скорости или частоте вращения соответствующих звеньев. , длина которых пропорциональна угловой скорости или частоте вращения соответствующих звеньев.Масштабный коэффициент угловой скорости определит величина отрезка PS: 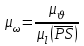 , ,а передаточное отношение 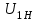 рассматриваемого механизма – отношение отрезков рассматриваемого механизма – отношение отрезков 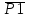 и и 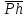 , то есть , то есть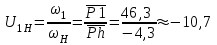 . .Расположение точек 2, 3 и h левее, а точек 1, 4 и 5 правее вертикали PS говорит о том, что колеса 2, 3 и водило Н вращаются в одном, а блок колес 4, 5 и колесо 1 – в обратном направлении, то есть передаточное отношение между зубчатым колесом 1 и водилом Н имеет знак «минус». 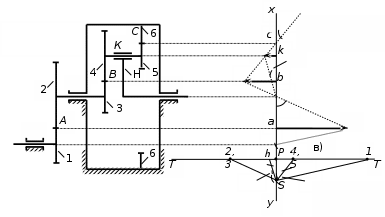 а) б) Рисунок 1.5 – Картина линейных и угловых скоростей Построения, выполненные на рисунке 1.5,в, позволяют определить передаточные отношения между любыми подвижными звеньями механизма. Расчетные значения передаточных чисел между входным и выходным звеньями, полученные графическим 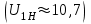 и аналитическим методом и аналитическим методом 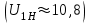 достаточно близки. достаточно близки. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||