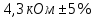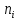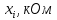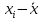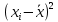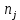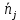Главная страница
Навигация по странице:

  • Классификационные признаки Мультиметр Резистр

    		•

    МСИС Многократные измерения. Классификационные признаки Мультиметр


    Скачать 1.01 Mb.
    НазваниеКлассификационные признаки Мультиметр
    АнкорМСИС Многократные измерения
    Дата16.05.2023
    Размер1.01 Mb.
    Формат файлаdocx
    Имя файлаlab4.docx
    ТипДокументы
    #1134478

    Цель работы:

    Приобретение навыков применения средств измерений и экспериментального определения их основных классификационных признаков;

    Изучение и освоение вероятностно-статистического метода обработки результатов многократных наблюдений;

    Приобретение навыков математической обработки результатов прямых равноточных измерений с многократными наблюдениями в соответствии с ГОСТ 8.736 и представления результата.

    Ход работы:


    Для измерения сопротивлений использовался мультиметр, заполним его классификационные признаки в таблице 1.

    Таблица 1 – Классификационные признаки мультиметра

    Классификационные признаки
    Мультиметр

    Резистр

    По видам (по техническому назначению)
    Измерительный прибор
    Мера однознчная

    По виду выходной величины
    Цифровой измерительный прибор



    По форме представления информации (только для измерительных приборов)
    Показывающий измерительный прибор



    По назначению
    для измерения постоянных и переменных напряжений и токов, электрического сопротивления постоянному току, электрической емкости, частоты, температуры.



    По метрологическому назначению
    Рабочее средство измерений
    Рабочее средство измерений

    Нормированные метрологические характеристики
    Точность указана на один год после калибровки при рабочей температуре от 18оС до 28 оС:

    Сопротивление:

    Диапазон

    Шаг
    Точность

    400 Ом
    0,1 Ом
    1.2%

    4000 Ом
    1 Ом
    1.2%

    40000 Ом
    10 Ом
    1.2%




    Номинальное значение:









    Вариационный ряд
    Границы интервалов группирования




    1
    4,26
    0,007
    0,000049
    4,24
    [4,240; 4,243]
    2
    0,066667

    2
    4,25
    -0,003
    0,000009
    4,24
    [4,240; 4,243]
    2
    0,066667

    3
    4,25
    -0,003
    0,000009
    4,25
    (4,247; 4,250]
    17
    0,566667

    4
    4,25
    -0,003
    0,000009
    4,25
    (4,247; 4,250]
    17
    0,566667

    5
    4,25
    -0,003
    0,000009
    4,25
    (4,247; 4,250]
    17
    0,566667

    6
    4,25
    -0,003
    0,000009
    4,25
    (4,247; 4,250]
    17
    0,566667

    7
    4,25
    -0,003
    0,000009
    4,25
    (4,247; 4,250]
    17
    0,566667

    8
    4,26
    0,007
    0,000049
    4,25
    (4,247; 4,250]
    17
    0,566667

    9
    4,25
    -0,003
    0,000009
    4,25
    (4,247; 4,250]
    17
    0,566667

    10
    4,26
    0,007
    0,000049
    4,25
    (4,247; 4,250]
    17
    0,566667

    11
    4,25
    -0,003
    0,000009
    4,25
    (4,247; 4,250]
    17
    0,566667

    12
    4,25
    -0,003
    0,000009
    4,25
    (4,247; 4,250]
    17
    0,566667

    13
    4,25
    -0,003
    0,000009
    4,25
    (4,247; 4,250]
    17
    0,566667

    14
    4,26
    0,007
    0,000049
    4,25
    (4,247; 4,250]
    17
    0,566667

    15
    4,25
    -0,003
    0,000009
    4,25
    (4,247; 4,250]
    17
    0,566667

    16
    4,25
    -0,003
    0,000009
    4,25
    (4,247; 4,250]
    17
    0,566667

    17
    4,26
    0,007
    0,000049
    4,25
    (4,247; 4,250]
    17
    0,566667

    18
    4,25
    -0,003
    0,000009
    4,25
    (4,247; 4,250]
    17
    0,566667

    19
    4,26
    0,007
    0,000049
    4,25
    (4,247; 4,250]
    17
    0,566667

    20
    4,26
    0,007
    0,000049
    4,26
    (4,257; 4,260]
    11
    0,366667

    21
    4,25
    -0,003
    0,000009
    4,26
    (4,257; 4,260]
    11
    0,366667

    22
    4,26
    0,007
    0,000049
    4,26
    (4,257; 4,260]
    11
    0,366667

    23
    4,26
    0,007
    0,000049
    4,26
    (4,257; 4,260]
    11
    0,366667

    24
    4,26
    0,007
    0,000049
    4,26
    (4,257; 4,260]
    11
    0,366667

    25
    4,24
    -0,013
    0,000169
    4,26
    (4,257; 4,260]
    11
    0,366667

    26
    4,25
    -0,003
    0,000009
    4,26
    (4,257; 4,260]
    11
    0,366667

    27
    4,26
    0,007
    0,000049
    4,26
    (4,257; 4,260]
    11
    0,366667

    28
    4,25
    -0,003
    0,000009
    4,26
    (4,257; 4,260]
    11
    0,366667

    29
    4,25
    -0,003
    0,000009
    4,26
    (4,257; 4,260]
    11
    0,366667

    30
    4,24
    -0,013
    0,000169
    4,26
    (4,257; 4,260]
    11
    0,366667




    4,253



    0,000963












    Проведя ряд независимых многократных измерений величины, запишем результат в таблицу 2.

    Таблица 2 – Результаты измерения и расчеты

    Вычислим среднее арифметическое значение: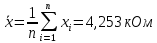



    Найдём среднее квадратичное отклонение результата измерений и оценку измеряемой величины: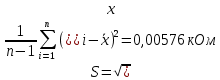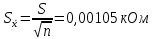





    Проверим наличие грубых погрешностей и исключим их с помощью критерия Граббса: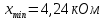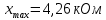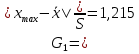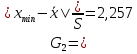









    Пусть доверительная вероятность P= 0,95, возьмём из таблицы критическое значения критерия Граббса 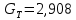. Оба коэффициента меньше критического, а значит промахов нет.

    Проверим гипотезу о нормальном распределении результатов наблюдений.

    Рассчитаем смещенное среднее квадратическое отклонение: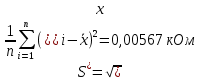



    Найдём коэффициент :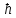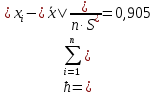



    Учтя, что уровень значимости α = 0.95, исходя из таблицы квантили равны .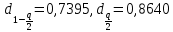

    Результаты измерений считаются распределенными по нормальному закону, если соблюдается условие: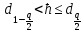



    Условие не соблюдается, а значит система не распределена по нормальному закону.

    Построим гистограмму, сперва определим количество интервалов: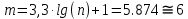



    Вычислим интервал группирования: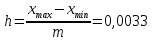



    Разобьём вариационный ряд на m интервалов и вычислим относительные частоты по формуле: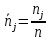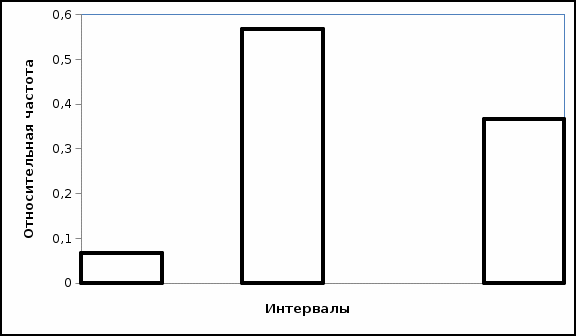





    Рисунок 1 – Гистограмма относительных частот

    Гистограмма подтверждает распределение не по нормальному закону.

    Определим доверительные границы случайной погрешности, приняв доверительную вероятность как P = 0,95.

    Найдём коэффициент Стьюдента, сперва рассчитаем коэффициент: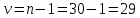



    Исходя из таблицы, коэффициент Стьюдента равен: .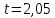

    Доверительные границы случайной погрешности определяются по формуле: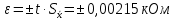



    Исходя из документации мультиметра, при измерении сопротивлений до 400 Ом граница не исключённой систематической погрешности равна: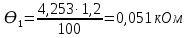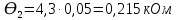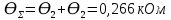







    Оценим доверительные границы погрешности оценки измеряемой величины. Найдём среднее квадратическое отклонение НСП: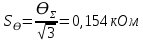



    Рассчитаем суммарное среднее квадратическое отклонение: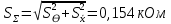



    Найдём коэффициент K: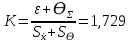



    Вычислим доверительную границу погрешности оценки измеряемой величины и запишем результат измерений: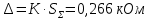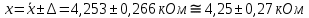




    Вывод:


    В результате выполнения лабораторной работы изучили вероятностно-статистический метод обработки результатов многократных измерений, получили опыт по применению средств измерений, а также по математической обработки результатов прямых равноточных измерений с многократными наблюдениями. Результат измерений был представлен в соответствии с МИ 1317.

    написать администратору сайта