Сумма углов треугольника 7 класс. пронюк 7 кл Сумма углов тр. Конспект урока геометрии в 7классе по учебнику А. В. Погорелова на тему "Сумма углов треугольника"

• Название: Конспект урока геометрии в 7классе по учебнику А. В. Погорелова на тему "Сумма углов треугольника"
• Анкор: Сумма углов треугольника 7 класс
• Дата: 11.11.2022
• Размер: 99.05 Kb.
• Имя файла: пронюк 7 кл Сумма углов тр.docx
• Тип: Конспект; #783173

Конспект урока геометрии в 7классе

по учебнику А.В. Погорелова

на тему:

"Сумма углов треугольника"

Выполнила:

Пронюк Ия Вячеславовна

Учитель математики ГБОУ Школа №1528

г. Москва, г. Зеленоград, 2019 г.

«Сумма углов треугольника».

Цели урока:

1. 
   Доказать теорему о сумме углов треугольника.
   
2. 
   Выполнить практические работы №1 и №2.
   
3. 
   Решать задачи на применение доказанной теоремы.
   

Оборудование: интерактивная доска, презентация, карточки.

• 
  План урока:
  
• 
  Организационный момент
  
• 
  Вводная беседа (историческая справка).
  
• 
  Объяснение нового материала.
  
  • 
    Практическое задание №1 (измерение углов треугольника).
    
  • 
    Практическое задание №2 (с треугольником из цветной бумаги).
    
  • 
    Доказательство теоремы о сумме углов треугольника.
    
• 
  Закрепление изученного материала.
  
• 
  Итог урока.
  

Ход урока

1. 
   Организационный момент
   

Объявляется цель урока, ход урока.

2. 
   Вводная беседа (историческая справка)
   

Рис.1 Пифагор (580-500 г.до н.э.)
Доказательство одной из важнейших теорем геометрии, теоремы о сумме углов треугольника приписывают Пифагору (580 – 500 г. г. до н. э.), которая была сформулирована так: «Сумма внутренних углов треугольника равна двум прямым углам»


Рис.2. Прокл (410-485 г. до н.э.)
Древнегреческий ученый Прокл (410 – 485 г.г. н.э.), комментируя первую книгу «Начал» Евклида, утверждал, что согласно Евдему Родосскому (IV в. до н.э.), написавшему первую в мире «Историю Математики», это доказательство было открыто пифогорейцами в V веке до н.э. Прокл в своих комментариях приводит доказательство, основанное на чертеже: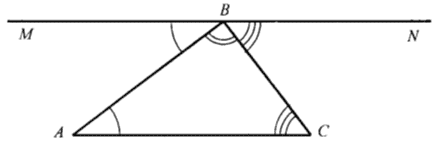

Рис. 3

Евклид (3 век до н.э)
Рис. 4.

В книге «Начала» Евклид излагает другое доказательство теоремы о сумме углов треугольника, которое легко понять с помощью чертежа:

Рис. 5.

3. 
   Объяснение нового материала
   

1. 
   Практическая работа №1. Учитель предлагает учащимся начертить в тетради произвольный треугольник АВС, измерить углы треугольника А, В и С (с помощью транспортира). Записать значения найденных углов и вычислить их сумму, т. е  А +  В +  С. Если измерения выполнены правильно, то сумма углов треугольника должна получиться равной 180.
   

2. 
   Практическая работа №2. У каждого на парте находиться треугольник из цветной бумаги. Учитель предлагает учащимся с помощью перегибаний листа бумаги (показанных на рисунке), убедиться, что сумма углов треугольника равна градусной мере развернутого угла, т. е. 180.
   

а) б)
в) г)
д)
Рис. 6.

3. 
   После выполнения практических заданий учащиеся сами формулируют утверждение теоремы о сумме углов треугольника.
   

4. 
   Учащиеся в тетради делает краткую запись доказательства теоремы:
   

Теорема: Сумма углов треугольника равна 180.



Рис. 7.
Дано: Δ АВС
Доказать:  А +  В +  С = 180.
Доказательство:

1. 
   Проведем через вершину В прямую ВD,
   

параллельную АС;

2. 
    1 =  4 как накрестлежащие, так как ВD ‌‌‌‌‌‌|| АС и АВ – секущая;
   
3. 
    3 =  5 как накрестлежащие, так как ВD ‌‌‌‌‌‌|| АС и ВС – секущая;
   
4. 
    4,  2 и  5 составляют развернутый угол;
   
5. 
    4 +  2 +  5 = 180, так как градусная мера развернутого угла равна 180, то
   
6. 
    1+ 2+ 3=180
   

4. 
   Закрепление изученного материала.
   

1. 
   Решить задачи устно:
   

(Чертежи высвечиваются на экране через проектор)
Задача 1. Найдите угол С.


Рис. 8
Задача 2. Найдите угол F.


Рис. 9
Задача 3. Найдите углы К и N.



Рис. 10

Задача 4. Найдите углы P и T.


Рис. 11

2. 
   Решить задачи с записью решения в рабочих тетрадях (к учебнику А.В. Погорелова) №18(1,2): Найти неизвестный угол треугольника, если у него два угла равны 1) 50◦ и 30◦; 2) 40◦ и 75◦. Ответы: 1) 100◦; 2)65◦.
   
3. 
   Решить задачу на доске и в тетрадях учащихся № 19(1,2).
   

№19(1)



Рис.12

№19(2) Найти углы треугольника, если они пропорциональны числам 2,3,4.(Ученик решает у доски). 2х+3х+4х=180, х=20. Ответ: 40◦,60◦,80◦.

4. 
   Самостоятельная работа по карточкам
   

Вычислить величины неизвестных углов в данных треугольниках и соедини стрелками чертежи с соответствующими ответами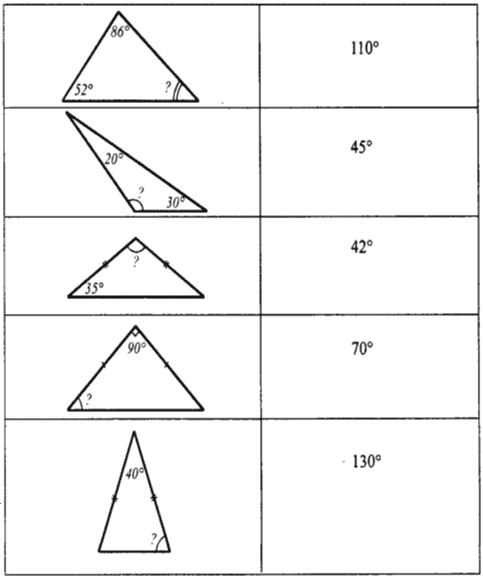



Рис.13

5. 
   Итог урока.
   

Домашнее задание:

1. 
   п.33, вопрос 9,10 стр. 52 учебника;
   
2. 
   № 18(3,4), № 19(3,4);
   
3. 
   РТ: № 264, № 266.
   

Список используемой литературы:

1. 
   Учебник «Геометрия 7-9» , автор А.В. Погорелов
   
2. 
   Рабочая тетрадь (Геометрия 7), автор Ю.П. Дудницын
   

Рисунки:

1. 
   Пифагор
   
2. 
   Прокл
   
3. 
   Доказательство Прокла
   
4. 
   Евклид
   
5. 
   Доказательство Евклида
   
6. 
   Практическая №1
   
7. 
   Доказательство теоремы
   
8. 
   9,10,11- Задачи на готовых чертежах
   
9. 
   12-решение задачи из учебника
   
10. 
    13-задачи на карточке