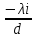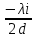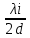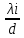Контрольная работа по дисциплине физика. кр 1. Контрольная работа 1 по дисциплине Физика (часть 2)
 Скачать 206.32 Kb. Скачать 206.32 Kb.
|
|
Министерство цифрового развития Федеральное государственное бюджетное образовательное учреждение профессионального образования Сибирский государственный университет телекоммуникаций и информатики Межрегиональный центр переподготовки специалистов Контрольная работа 1 по дисциплине «Физика (часть 2)» Выполнил: Матвеев А.А. Группа: ИСТ-22 Вариант: 1 Проверил: Моргачев Ю.В. Новосибирск 2023 1 - ВАРИАНТ 1. В опыте Юнга вначале рассматривается излучение с длиной волны λ1 = 0,7 мкм, а затем с λ2. Определите значение длины волны λ2, если шестая светлая полоса в первом случае совпадает с девятой темной полосой во втором случае. Рисунком поясните схему опыта Юнга, укажите на рисунке распределение интенсивности света на экране. Опыт проводится в вакууме. Дано: 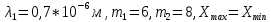 Найти: 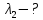 Решение: 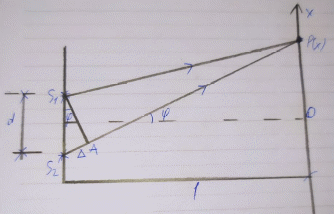 Где 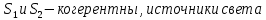 d- Расстояние между ними Расстояние от источника до экрана 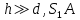 является волновым фронтом. Поэтому разность хода образуется на расстояние является волновым фронтом. Поэтому разность хода образуется на расстояние 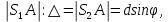 т.к. т.к. 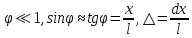 Светлая полоса возникает если « 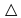 » содержит целое число длины волн: » содержит целое число длины волн: 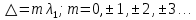 - целое число. - целое число.Тёмная полоса возникает если «∆» содержит нечетное число полудлин волн; 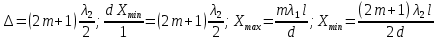 По условию 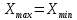 . .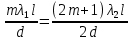 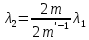 Центральную светлую полосу не будем считать. Тогда m=6. Первый минимум соответствует 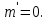 9-й минимум соответствует 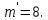 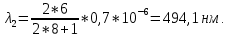 Если интенсивность источников равны 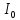 то интенсивность света в точке наблюдения то интенсивность света в точке наблюдения 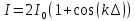 Где, 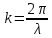 - волновой центр, - волновой центр, 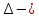 оптическая разность хода. оптическая разность хода.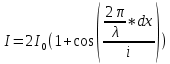 I(x) будет изменятся по закону косинуса вокруг 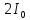
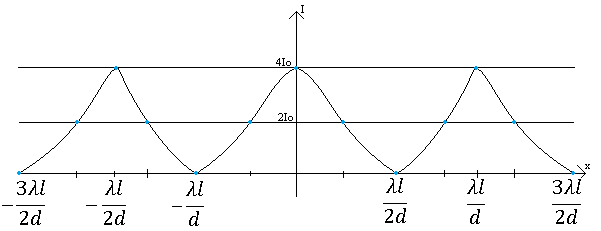 Ответ:  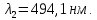  2. Монохроматический свет падает нормально на щель шириной 10 мкм. За щелью находится тонкая линза с оптической силой 4Дптр. В фокальной плоскости линзы расположен экран. Найти длину волны света 𝜆, если расстояние между симметрично расположенными минимумами второго порядка равно 6 см. Приведите рисунок для схемы установки. Изобразите дифракционную картину интенсивности света на экране. Пронумеруйте все дифракционные максимумы, которые могут быть видны на экране. Дано: b=10 мкм; k=2; D=4 Дптр; x=3 см. Найти: λ-? Решение: 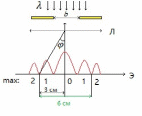 Нам нужно найти длину волны λ. Ее мы можем выразить из условия наблюдения дифракционного минимума: 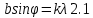 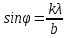 Где k, порядок дифракционного минимума, у нас по условию k=2. Фокусное расстояние линзы определим из ее оптической силы: 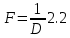 Из формул 2.1 и 2.2 мы можем вывести формулу для расстояния от центра дифракционной картины до минимума второго порядка: 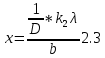 Нам дано расстояние между симметрично расположенными минимумами второго порядка = 6 см, но для 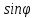 нам нужно расстояние от центра дифракционной картины до минимума второго порядка, которое исходя из рисунка является нашим катетом. нам нужно расстояние от центра дифракционной картины до минимума второго порядка, которое исходя из рисунка является нашим катетом.Отсюда: 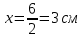 Выразим из 2.3 длину волны λ: 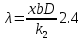 Подставим числовые значения: 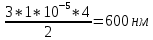 Ответ: длина волны λ = 600 нм. 3. Красная граница фотоэффекта рубидия λ0=0,81 мкм. Определить скорость фотоэлектронов при облучении рубидия монохроматическим светом с длиной волны λ=0,4 мкм. Какую задерживающую разность потенциалов Uз надо приложить к фотоэлементу, чтобы прекратить фототок? На сколько изменится задерживающая разность потенциалов ΔUз при увеличении длины волны падающего света на Δλ=200 нм? Изобразите на рисунке вольтамперную характеристику фотоэффекта (ВАХ); покажите на ВАХ ток насыщения и задерживающий потенциал. Дано: 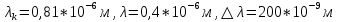 Найти: 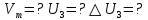 Решение: По закону Эйнштейна для фотоэффекта: 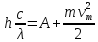 где h - постоянная планка, с – скорость света в вакууме, 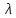 – длина волны, – длина волны,m – масса электрона, 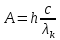 – работа выхода; – работа выхода;Производим замену переменных и запишем формулу: 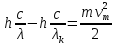 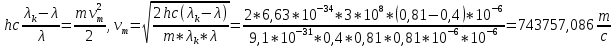 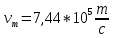 По теореме о кинетической энергии, изменение кинетической энергии равно работе электрических сил: 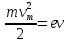 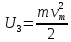 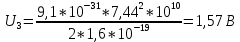 При увеличении длины волны на 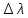 формула Эйнштейна будет таким: формула Эйнштейна будет таким: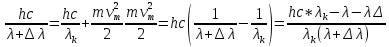 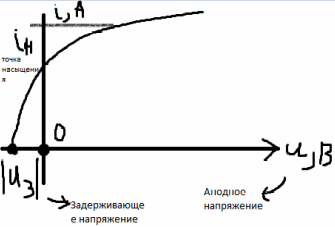 Зависимость силы фототока от анодного напряжения, ( 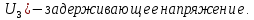 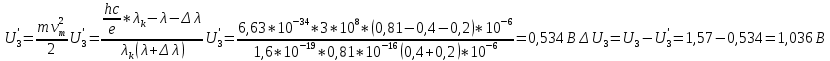 Ответ: 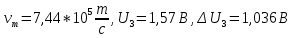 . . 4. Температура абсолютно черного тела увеличилась в 1,5 раза, в результате чего длина волны 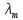 , на которую приходится максимум энергии излучения, изменилась на , на которую приходится максимум энергии излучения, изменилась на 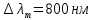 . Определить начальную . Определить начальную 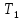 и конечную и конечную 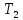 температуру тела. Во сколько раз в результате нагревания изменилась тепловая мощность, излучаемая телом? Рисунком поясните график распределения энергии в спектре излучения абсолютно чёрного тела, укажите для данных температур положение температуру тела. Во сколько раз в результате нагревания изменилась тепловая мощность, излучаемая телом? Рисунком поясните график распределения энергии в спектре излучения абсолютно чёрного тела, укажите для данных температур положение 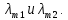 Дано: 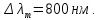 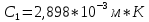 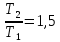 Найти: 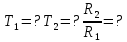 Решение: 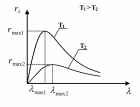 Воспользуемся законом смещения Вина: длина волны, на которую приходится максимум излучательной способности а.ч.т. 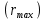 обратно пропорционален абсолютной температуре этого тела. Для любого а.ч.т. постоянная обратно пропорционален абсолютной температуре этого тела. Для любого а.ч.т. постоянная 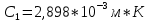 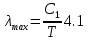 По условию задачи температура абсолютно черного тела увеличилась в 1.5 раза: 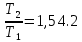 Следовательно: 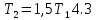 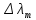 определяется как разница между определяется как разница между 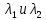 : :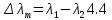 Выразим 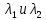 : :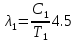 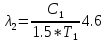 Подставим 4.5 и 4.6 в 4.4: 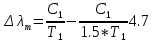 Выразим температуру первого тела 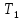 , для этого для начала приведем , для этого для начала приведем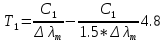 Подставим наши данные: 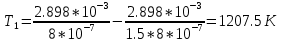 Зная 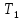 , мы можем найти , мы можем найти 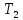 , подставив значение , подставив значение 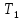 в 4.3: в 4.3: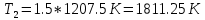 Согласно закону Стефана – Больцмана, энергетическая светимость R абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры. 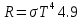 Где 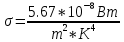 – постоянная Стефана-Больцмана. – постоянная Стефана-Больцмана.Определим, во сколько раз в результате нагревания изменилась тепловая мощность, излучаемая телом. Для этого определим отношение 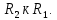 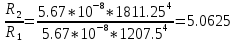 Ответ: 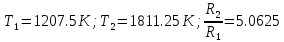 5. Свободный электрон, имея кинетическую энергию 15 эВ, неупруго столкнулся с атомом водорода, находящимся в основном состоянии, и отскочил от него, потеряв часть энергии. Энергия электрона после столкновения оказалась 2.91 эВ. Определить длины волн, которые может излучить атом водорода после столкновения с электроном. Изобразите на рисунке энергетическую диаграмму атома водорода, покажите на ней все переходы между уровнями, которые могут произойти после столкновения. Дано: T=15 эВ, 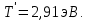 Найти: 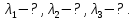 Решение: Энергия электрона в атоме водорода определяется формулой 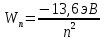 Где -13,6 эВ – энергия основного состояния, n – главное квантовое число. После получения дополнительной энергии 12,09 эВ электрон с основного состояния (h=1) перейдёт в состоянии с «n»: 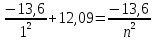 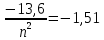 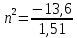 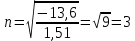 n=3, то электрон перейдёт в состояние с n=3. 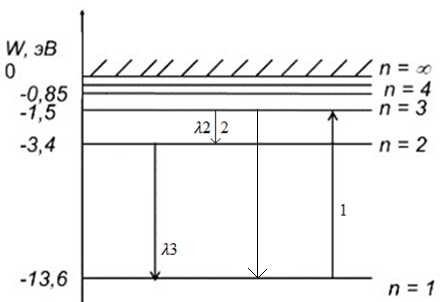 По формуле Бора соответствующее излучение имеет длину волны: 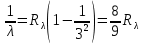 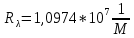 Постоянная Ридберга: 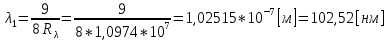 После столкновения может произойти переход: 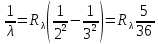 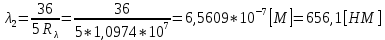 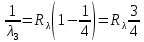 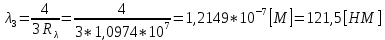 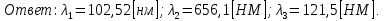 6. При увеличении энергии электрона на 300 эВ его дебройлевская длина волны изменилась в 2 раза. Найти первоначальную длину волны электрона. В этой задаче нет векторных величин. Длина волны де Бройля определяется по формуле: λ=hm*v λ0= 2λ v=2v0 Ek=m*v22=4m*v022=m*v022+300 m*v022=300эВ3=100 эВ λ0= hm*v0=h2E kom= 6.62*10-842*300*1.6*10-16*9.1*10-3=6.62*10-8493.5*10-25=0.07*10-9 м Ответ: : λ0= 0.07*10-9 м. 7. Образец германия с собственной проводимостью при температуре 300 К имеет удельное сопротивление 𝜌 = 0,5 Ом ⋅ м. Подвижность электронов 𝜇𝑛 =0,38 м2 Вс, подвижность дырок 𝜇𝑝 =0,19 м2 Вс, 𝜀 =16. 1. Определить концентрацию собственных носителей заряда. Начертить энергетическую диаграмму, указав положение свободных и связанных электронов, положение дырок. 2. Определить ширину запрещённой зоны Δ𝑊, считая, что в условии задачи плотность состояний в зоне проводимости и в валентной зоне 𝑁𝑐 = 𝑁𝑣 = 2,5 ⋅ 1025м −3 . 3. Найти величину плотности дрейфового тока через образец, если напряжённость поля Е=200 В/м. Удельная проводимость полупроводника: σ=e(pi*μp+ni*μn) e-заряд электрона p-концентрация дырок n-концентрация электронов Удельная проводимость и удельное сопротивление связаны следующей формулой: σ=1ρ Так как полупроводник с собственной проводимостью, то pi=ni Тогда σ=eniμp+μn=1ρ pi=ni=1eρμp+μn=11,6*10-19*0,5*(0,19+0,38)=2,2*1019м-3 Энергетическая диаграмма Концентрация собственных носителей заряда и плотности состояний связаны следующей формулой: ni=Nc*Nv*e-ΔW2kT Прологарифмируем формулу: ln(ni)=ln(Nc*Nv*e-ΔW2kT) ln(ni)=ln(Nc*Nv+ln(e-ΔW2kT) ln(ni)=ln(Nc*Nv)-ΔW2kT ΔW2kT= ln(Nc*Nv-ln(ni) ΔW2kT=lnNc*Nvni ΔW=2kT*lnNc*Nvni k-постоянная Больцмана ΔW=2*1,38*10-23*300*ln2,5*1025*2,5*10252,2*1019=1,15*10-19 Дж Удельная проводимость и плотность дрейфового тока связаны следующей формулой: σ=JдрE Jдр= σ*E=1ρ*E=Eρ=2000,5=1000 Aм2 Ответ: pi=ni=2,2*1019м-3 ΔW=1,15*10-19 Дж Jдр=1000 Aм2 |