1-33_Радиоавтоматика. Контрольная работа 1 по дисциплине Радиоавтоматика (Учебное пособие Радиоавтоматика, авторы В. П. Пушкарев, Д. Ю. Пелявин., 2004г.)
 Скачать 0.59 Mb. Скачать 0.59 Mb.
|
|
Министерство образования Российской Федерации Томский межвузовский центр дистанционного образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра радиоэлектроники и защиты информации (РЗИ) КОНТРОЛЬНАЯ РАБОТА № 1 по дисциплине «Радиоавтоматика» (Учебное пособие «Радиоавтоматика», авторы В.П. Пушкарев, Д.Ю. Пелявин., 2004г.) Тема работы: Исследование типовых радиотехнических звеньев и структурные преобразования систем радиоавтоматики. Вариант 33 Выполнил: студент ТМЦДО 2005г Содержание Задание №1…………………………………………………………3Задание №2…………………………………………………………6 Задание №3………………………………………..………………..9 Задание №4 ……………………….………………..………………12 Задание №1Д 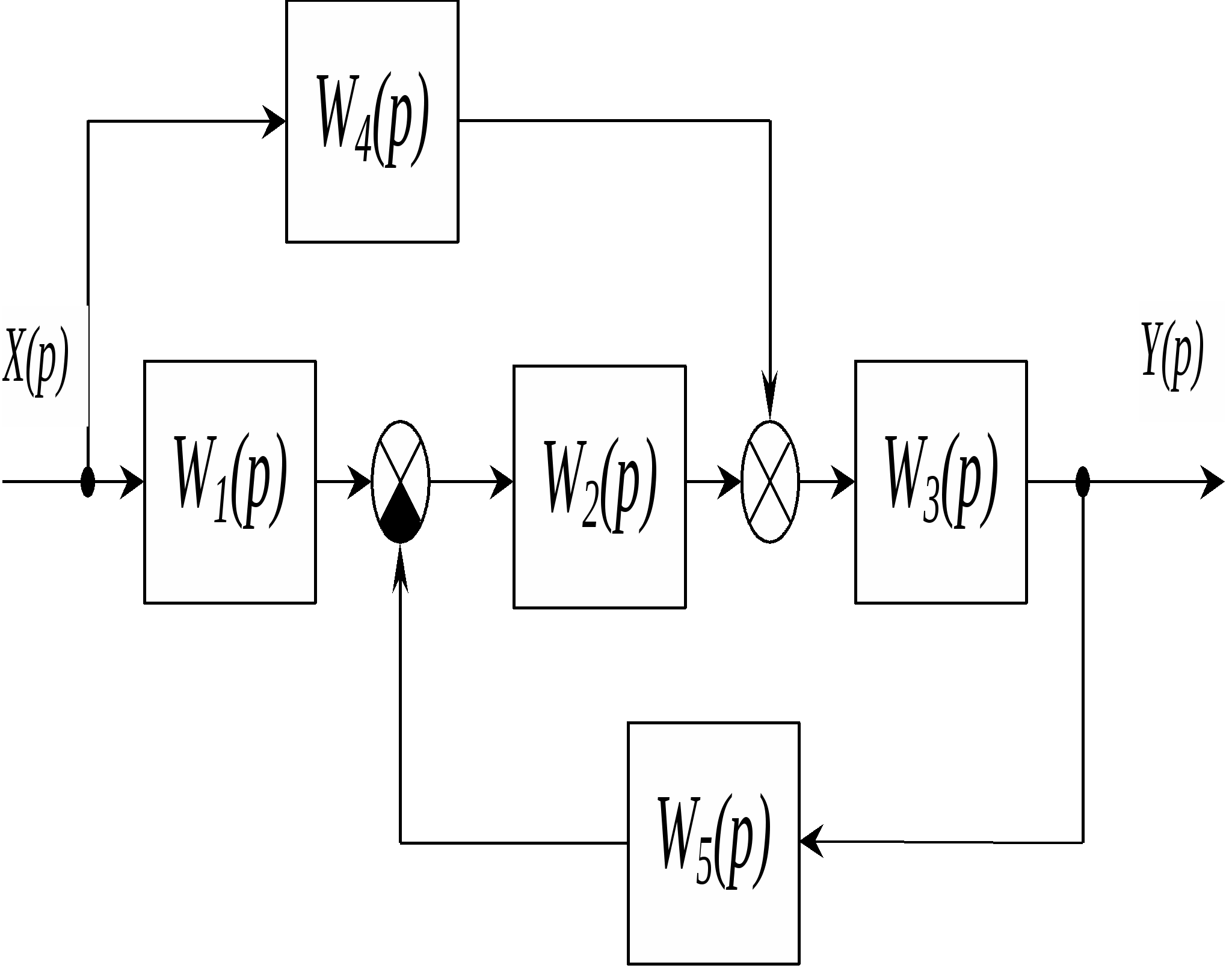 ля выполнения задания необходимо преобразовать структурную схему системы радиоавтоматики и получить передаточную функцию системы в общем виде. Структурная схема исследуемой системы показана на рисунке 1.1. Вид типовых радиотехнических звеньев исследуемой системы выбирается из таблицы 1.1, параметры звеньев из таблицы 1.2. Рисунок 1.1 Структурная схема системы Таблица 1.1 Вид типовых радиотехнических звеньев
Таблица 1.2 Параметры элементов схемы: (W1, W2, W3).
Передаточную функцию системы радиоавтоматики необходимо выразить в виде отношения полиномов Решение. Последовательность преобразования структурной схемы (рис. 1.1), на основе правил структурных преобразований, представляется следующим алгоритмом: перенос сумматора через звено с передаточной функцией W2(p) (рис. 1.2, а); свертывание последовательного соединения звеньев W2(p) и W3(p), свертывание параллельного соединения звеньев W1(p) и W4(p)/ W2(p), свертывание встречно-параллельного соединения звеньев W5(p) и W2(p)* W3(p) (рис. 1.2, б); свертывание последовательного соединения полученных звеньев. 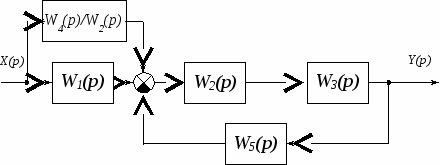 а) 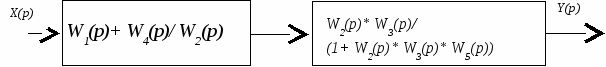 б)Рисунок 1.2 Преобразование структурной схемы системы После структурных преобразований системы РА определим передаточную функцию для системы с обратной связью и представим в виде аналитического выражения: Далее подставим значения звеньев структурной схемы из таблицы 1.1 и получим: 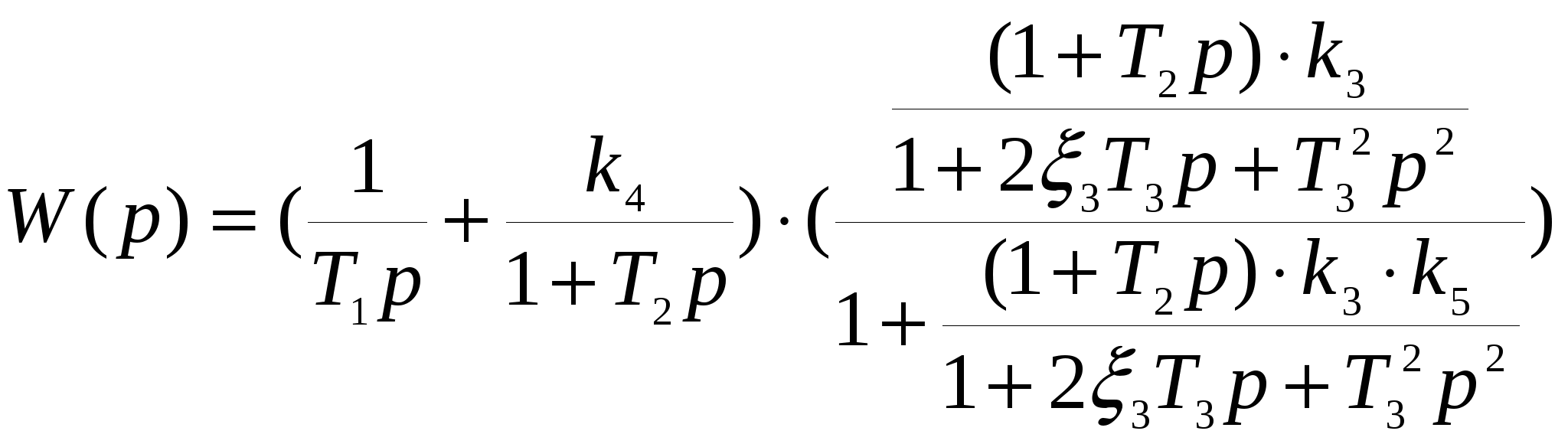 И после преобразований получим: |
Передаточная функция | k | T | T1 | T2 | T3 |
| | 15 | 0.05 | 0.5 | 5 | 0.5 |
Решение.
Заданная передаточная функция представляется в виде произведения типовых звеньев:
Коэффициент передачи системы в децибелах по формуле
k[дБ]=20 lg k и сопрягающие частоты звеньев, входящих в систему по формуле:
Таблица 2.2
| Коэффициенты | K [раз] | T | T1 | T2 | T3 |
| 15 | 0,05 | 0,5 | 5 | 0,5 | |
| Постоянные времени | k [дБ] | ω | ω1 | ω2 | ω3 |
| 23,5 | 20 | 2 | 0,2 | 2 |
В логарифмическом масштабе построим графики входящих в систему «типовых» звеньев. Диапазон частот графика выберем из условия: минимальная частота равна не более одной десятой самой меньшей сопрягающей частоты, а максимальная частота в десять или более раз больше максимальной: от ω2/10 = 0,02 до ω*10 = 200 Герц. Построим оси и отметим сопрягающие частоты звеньев:
Р
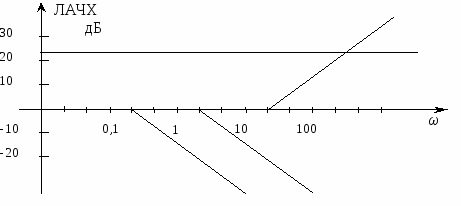
исунок 2.1 Логарифмические характеристики типовых радиотехнических звеньев, входящих в исследуемую систему
В нашей системе присутствует одно дифференцирующее звено первого порядка и три инерционных звена.
П
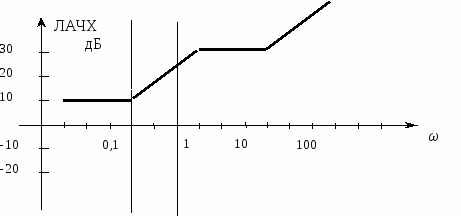
остроим АЧХ всех звеньев системы на одном графике, рисунок 2.1, затем «сложим координаты» всех графиков в децибелах, чтобы получилась одна кривая (рисунок 2.2).
Рисунок 2.2 Суммарная логарифмическая характеристика
исследуемой системы
А
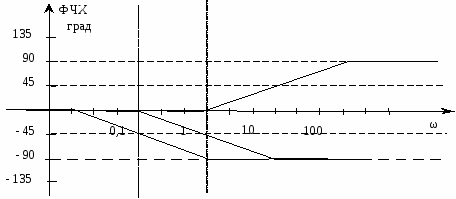
налогично поступаем при построении ФЧХ системы (рисунок 2.3 и 2.4).
Рисунок 2.3 Фазовые характеристики входящих в исследуемую
систему типовых звеньев
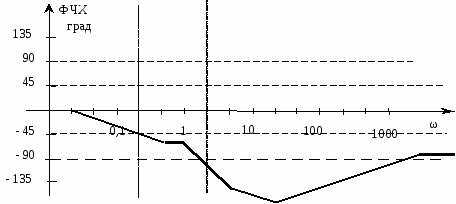
Рисунок 2.4 Суммарная фазовая характеристика исследуемой системы
Ответ на второе задание (точки перегиба АЧХ и ФЧХ):
АЧХ : 10 дБ, 0.2 Гц; 30 дБ, 2 Гц; 30 дБ, 20 Гц.
ФЧХ: 0о, 0.02 Гц, –45о, 0.5 Гц, 0о, 1 Гц, –90о, 5 Гц, –45о, 20 Гц, +45о, 1200 Гц, 0о.
Задание №3
Исследовать на устойчивость и определить запасы устойчивости, по заданному в таблице 3.1 параметру, замкнутой системы управления по заданной передаточной функции разомкнутой системы РА, которая находится в таблице 2.1, а параметры и критерий устойчивости приведены в таблице 3.1.
Таблица 3.1
| k | T | T1 | T2 | T3 | ξ | Критерий | Параметр |
| 15 | 0.05 | 0.5 | 5 | 0.5 | 0.5 | Гурвица | T |
Результат необходимо привести в смешанном виде – текст (устойчива – неустойчива) и число запасов устойчивости по заданному параметру (для критерия Гурвица).
Решение.
Передаточная функция разомкнутой системы РА:
Числитель и знаменатель передаточной функции
отсюда:
a0=k;
a1=kT;
a2=0;
a3=0.
и аналогично для знаменателя:
B(p)=T1T2T3p3+(T1T2+T1T3+T2T3)p2+(T1+T2+T3)p+1
b0=1;
b1= T1+T2+T3;
b2= T1T2+T1T3+T2T3;
b3= T1T2T3.
Из таблицы 3.1, подставим коэффициент передачи и постоянные времени:
a0=15;
a1=0.75;
a2=0;
a3=0.
b0=1;
b1= 6;
b2= 5.25;
b3= 1.25.
Запишем разомкнутую передаточную функцию:
Для исследования устойчивости системы согласно критерию Гурвица замкнем систему, для этого воспользуемся формулой для замкнутой системы:
D(p)=(a3+b3)p3+(a2+b2)p2+(a1+b1)p+a0+b0
Подставив полученные ранее коэффициенты, получим:
D(p)=(0+1.25)p3+(0+5.25)p2+(0.75+6)p+15+1,
D(p)=1.25p3+5.25p2+6.75p+16
з
 атем заполним «матрицу Гурвица», порядок которой совпадает с порядком системы (в нашем случае третий), где
атем заполним «матрицу Гурвица», порядок которой совпадает с порядком системы (в нашем случае третий), где D(p)=c3 p3+c2 p2+c1 p+c0
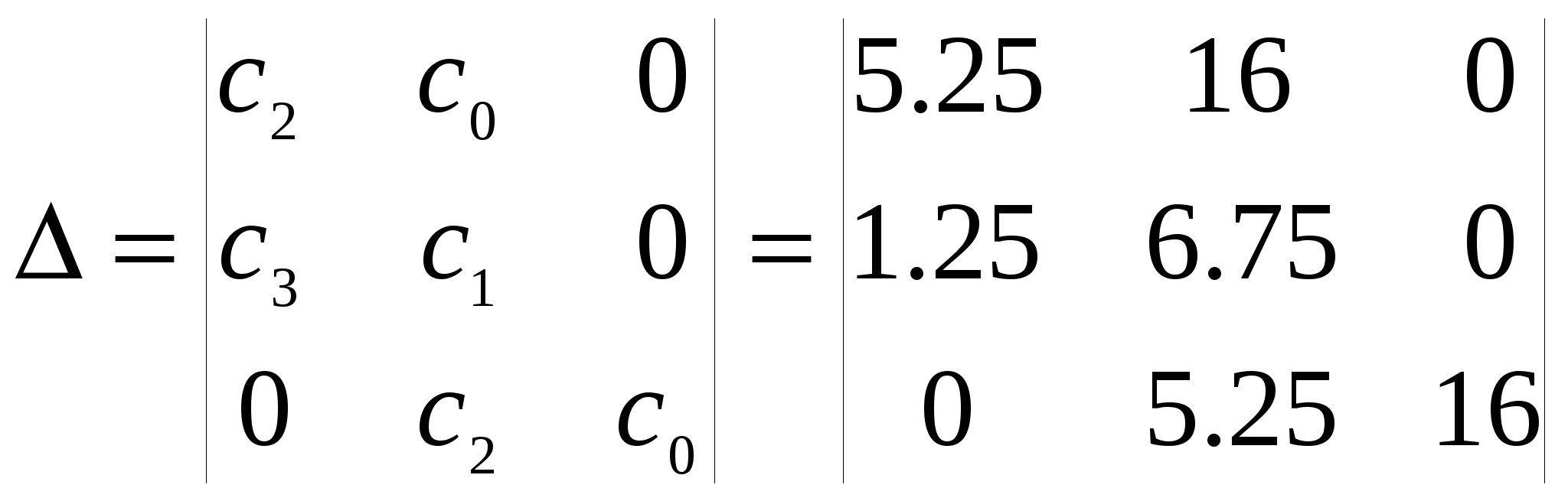
Для определения устойчивости, согласно критерию Гурвица, необходимо, чтобы все элементы матрицы имели один знак и все главные миноры (определители) матрицы были положительны.
Все определители положительны, следовательно, система устойчива.
Найдем запасы устойчивости по постоянной времени Т, для этого в характеристическое уравнение не надо подставлять значение этого параметра, тогда:
a1=15T;
Остальные коэффициенты не изменятся, значит:
D(p)=1.25p3+5.25p2+(15Т+6)p +16
заполним «матрицу Гурвица»:
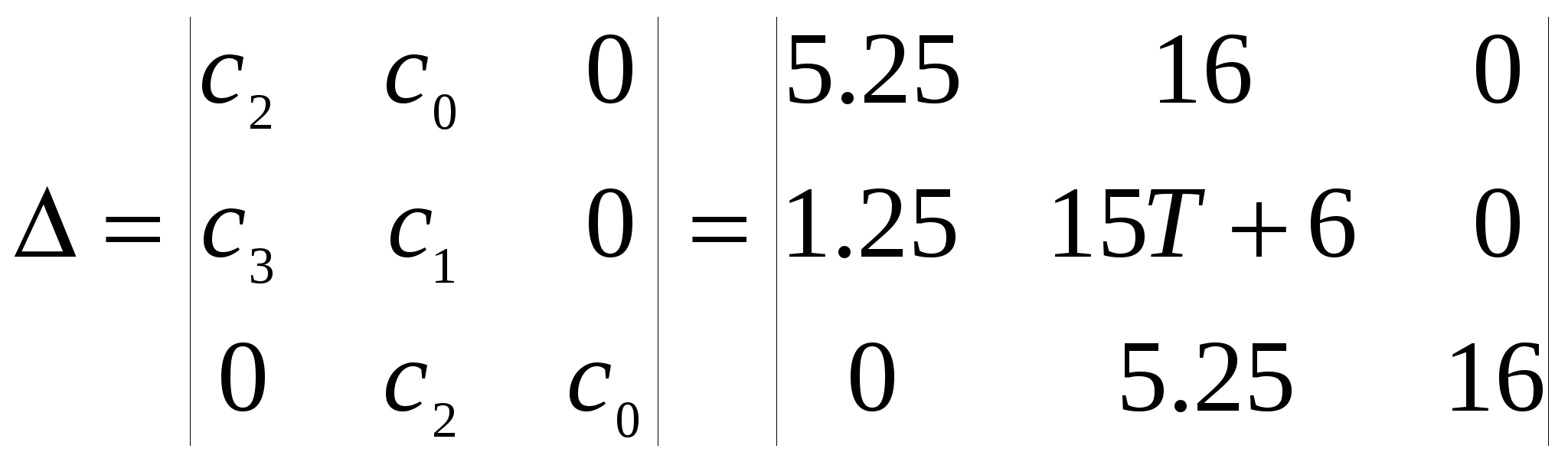
тогда главные определители матрицы:
T> - 0.146.
T> - 0.146.
Начальные неравенства справедливы при T> - 0.146.
Ответ: система устойчива, запас устойчивости по постоянной времени Т, простирается от –0.146 до бесконечности (–0.146, ∞).
Задание №4
Определить время переходного процесса по переходной характеристике системы (рисунок 4.1).
Данные: Δh=1, Δt=0.3, δ=10%.
Р
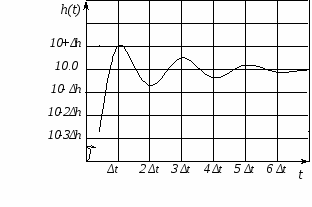
исунок 4.1 График переходного процесса
Решение.
Длительность переходного процесса tп определяется как интервал времени от момента подачи единичного сигнала на вход исследуемой системы до того момента, когда отклонение выходного сигнала от установившегося значения не будет превышать величину заданной ошибки системы δ.
Установившееся значение по данному графику будет на уровне значения 10.0, соответственно отклонение выходного сигнала от установившегося значения на величину ошибки системы δ=10% равно 10.01.0, или 10.0 Δh. Этому значению, по графику, соответствует длительность переходного процесса Δt=0.3 с.
Ответ: 03.

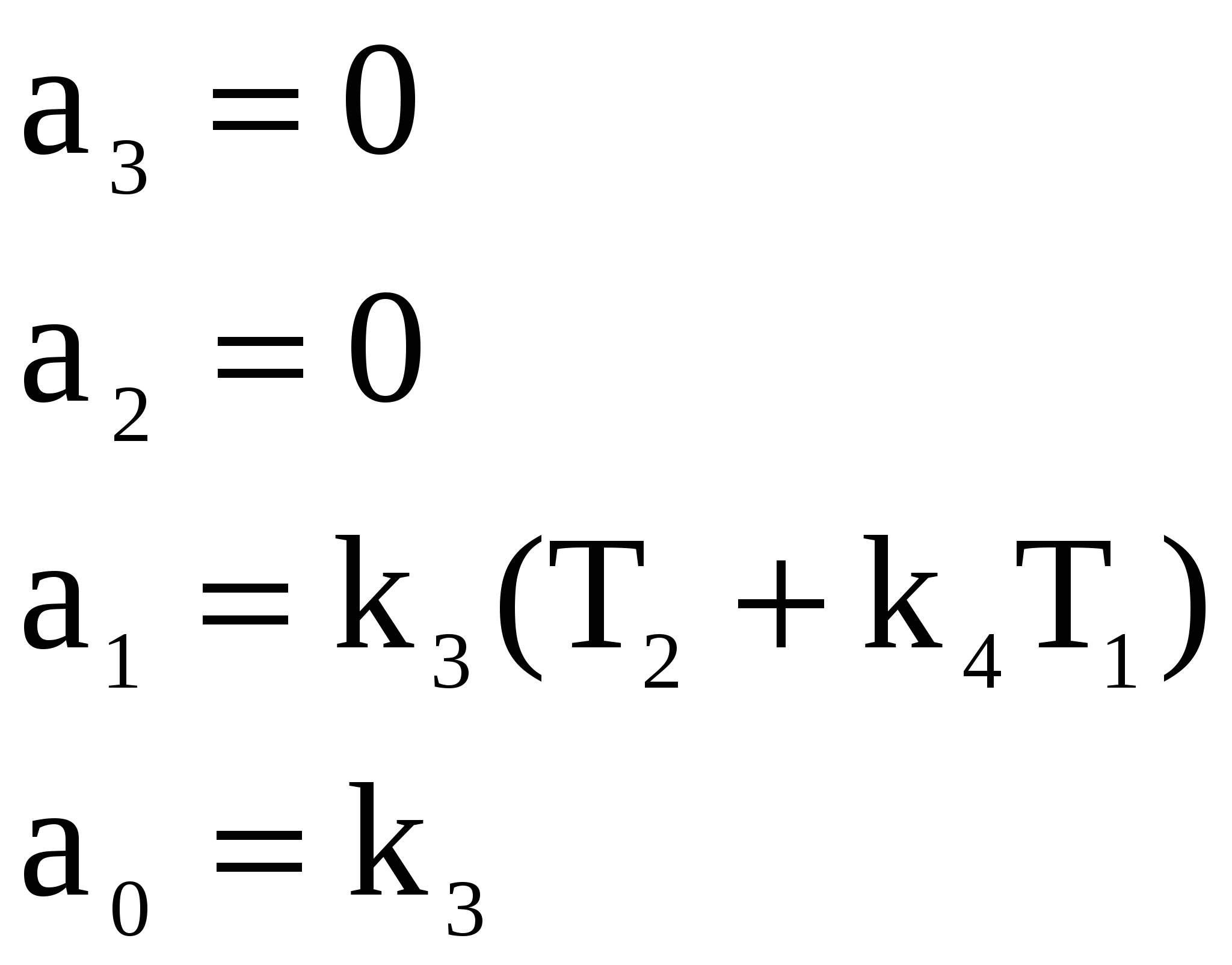 и
и 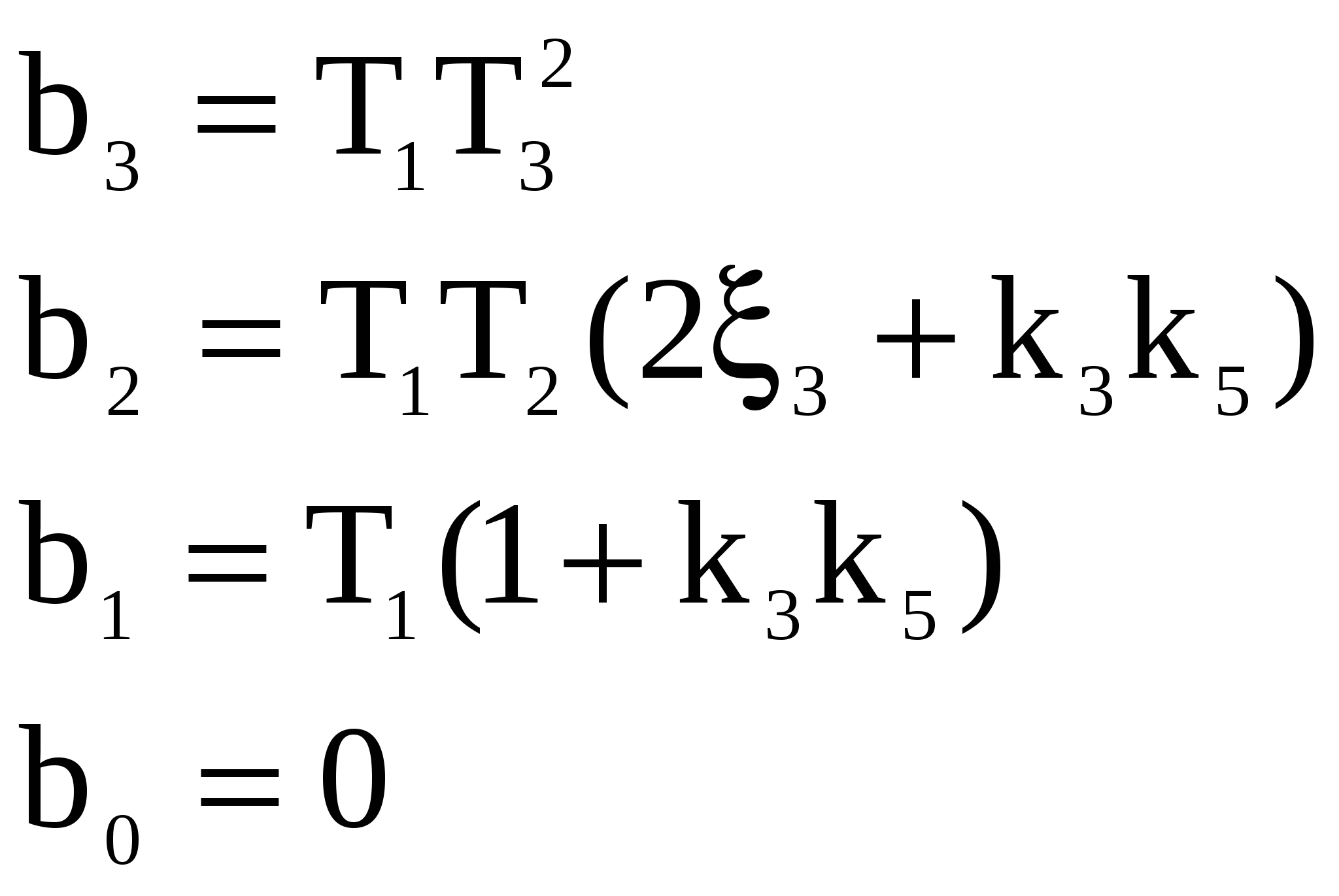
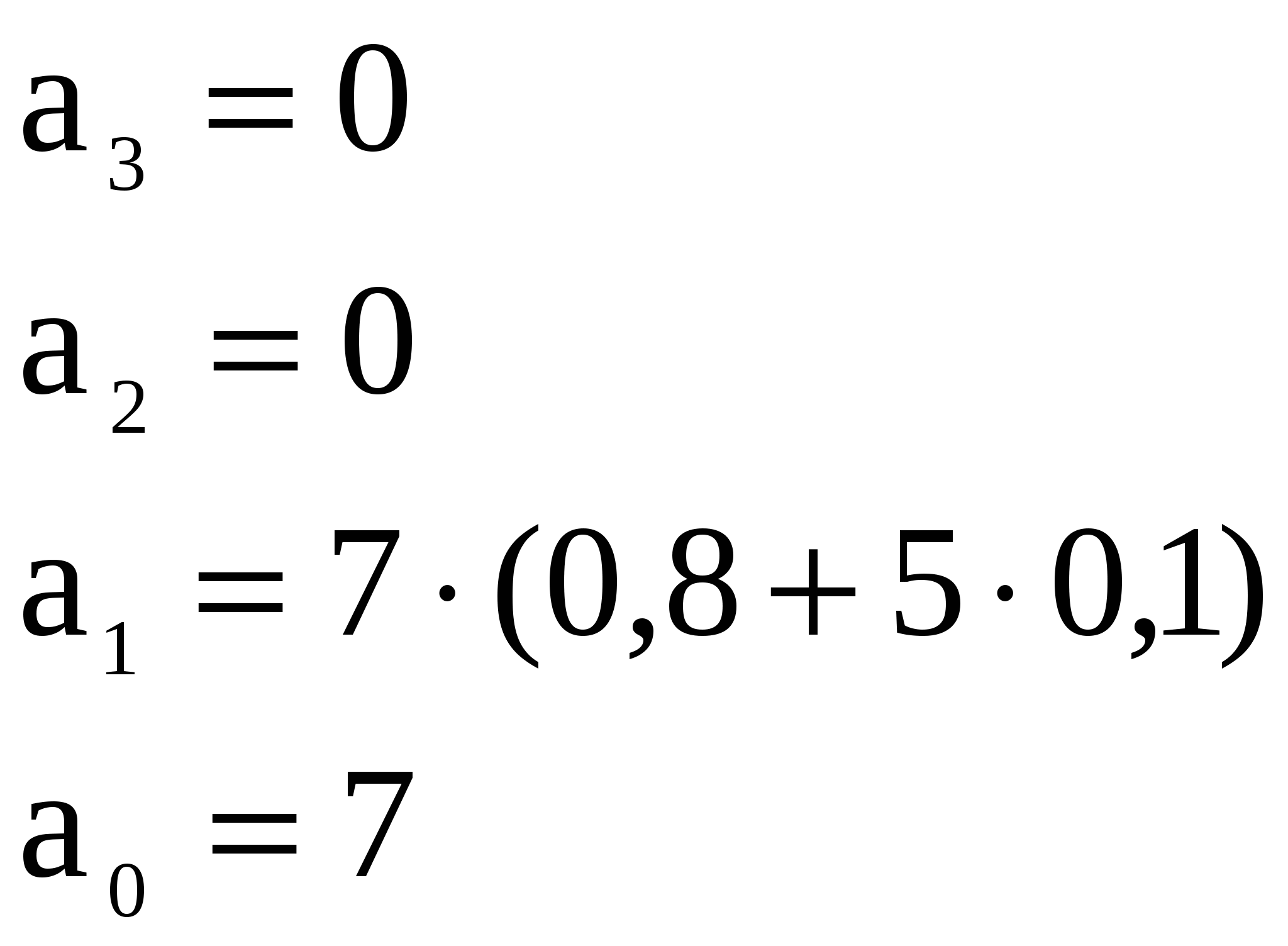 и
и