ТУСУР Контрольная работа по математике №2 вар5. Текстовая контрольная работа № 2. Контрольная работа 2 Вариант 5 Студент группы " " 2022 г
 Скачать 89.79 Kb. Скачать 89.79 Kb.
|
Министерство науки и высшего образования Российской ФедерацииФедеральное государственное бюджетное образовательное учреждениевысшего образованияТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТСИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)Кафедра автоматизированных систем управления (АСУ) Линейная алгебра Аналитическая геометрия Контрольная работа №2 Вариант 5
1(Д01.РП). Составьте общее уравнение прямой, проходящей через точку M(1, 4) параллельно прямой 2x + 3y + 5 = 0. Решение: Уравнение прямой Ax+By+C=0 поэтому в качестве вектора нормали принимаем вектор N=(2,3). Уравнение: 2x+3y-14=0. Ответ: 2x+3y-14=0. 2 (3А2.РП). Найдите координаты проекции точки M(3, 6) на прямую x + 2y − 10 = 0. Решение: Точка G проекция точки М на данную прямую, её можно найти, как точку на пересечении прямых x+2y-10=0 и МG, которая перпендикулярна к данной и проходящей через точку М. Прямая МG параллельна вектору 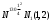 нормали прямой х+2у-10=0. В качестве вектора нормали прямой МР можно принять вектор нормали прямой х+2у-10=0. В качестве вектора нормали прямой МР можно принять вектор 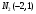 , а потому уравнение прямой МР имеет вид -2x+y-(-6+6)=0 или 2x+y=0. Для отыскания координат точки Р мы получили систему: , а потому уравнение прямой МР имеет вид -2x+y-(-6+6)=0 или 2x+y=0. Для отыскания координат точки Р мы получили систему: x+2y-10=0 2x-y=0 Решим систему: X=10-2y, x=10-2y, x=10-2y, x=2. Ответ: (2,4). 3. (103.БЛ). Запишите общее уравнение плоскости, проходящей через три заданные точки M1(−6, 1,−5), M2(7,−2,−1), M3(10,−7, 1). Решение: Данная плоскость параллельна векторам 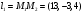 и и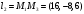 . Поэтому в качестве вектора нормали можно принять вектор . Поэтому в качестве вектора нормали можно принять вектор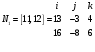 Разложим этот определитель по элементам первой строки: N= |-3 4| |13 4| |13 -3| |-8 6| * i - |-16 6|* j +|16 -8|* k=14i-14j-56k. N=(14, -14, -56) или N=(1, -1, -4). Запишем уравнение плоскости х-у-4z+c=0. Для определения C используем условие, что плоскость проходит через точку 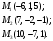 Найдём значение в этих точках: М1= 6+1-20 = -13; М2= -7-2-4 = -13; М3= -10-7+4 = -13. Уравнение х-у-4z-13=0 является искомым. Ответ: х-у-4z+13=0. 4 (203). Известно, что прямая L параллельна вектору l = (0, 6, 8). Найдите длину отрезка этой прямой между плоскостями x + y + z − 3 = 0 и x + y + z − 24 = 0. Решение: Запишем систему: 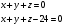 Тогда: 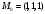 Значит: 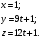 Теперь найдём длину отрезка прямой между плоскостями. 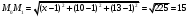 Ответ:15. 5(3С2). Некоторая прямая проходит через точку P(2, 2, 1), пересекает ось ординат в точке Q(0, y₀, 0) и пересекает прямую 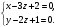 Найдите y₀. Найдите y₀.Решение: Составим уравнение прямой, проходящей через точки Р и Q: 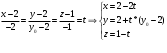 Найденные x, у, z подставляем в систему: 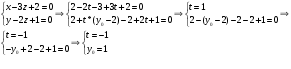 y₀=1 Ответ:1. 6(7АД). Плоскость содержит прямую 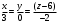 и параллельна прямой x−3 = y−3 = −2(z−6). Найдите квадрат расстояния от второй прямой до плоскости. и параллельна прямой x−3 = y−3 = −2(z−6). Найдите квадрат расстояния от второй прямой до плоскости.Решение: Из уравнения первой прямой находим, что она проходит через точку М (0; 0; 6) с направляющим вектором 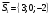 Из уравнения второй прямой находим, что она имеет направляющий вектор 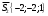 Уравнение искомой плоскости находим, как уравнение, проходящее через точку (0;0;6) с вектором нормали 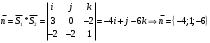 Тогда: -4(x-0)+1*(y-0)-6*(z-6)=0 -4x+y-6z+36=0 Ответ: -4x+y-6z+36=0. 7(C04.РП). Докажите, что уравнение x² + y² + 6x − 10y − 15 = 0 определяет на плоскости XOY окружность. Найдите её центр и радиус R. В ответе сначала указать x0, y0 координаты центра, затем R. Решение: Выделим полные квадраты. (x+3)²+(y-5)²-9-25-15=0; (x+3)²+(y-5)²=49; Тогда координаты центра (x₀, y₀) = (- 3; 5), R=7 Ответ: -3, 5, 7. 8. Дана кривая 4x 2 − y 2 − 24x + 4y + 28 = 0. 8.1. Докажите, что эта кривая — гипербола. 8.2(325.Б7). Найдите координаты её центра симметрии. 8.3(Д06.РП). Найдите действительную и мнимую полуоси. 8.4(267.БЛ). Запишите уравнение фокальной оси. 8.5. Постройте данную гиперболу. Решение: Выделим полные квадраты из уравнения. 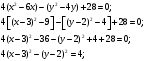 Тогда уравнение примет вид: 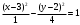 гипербола. гипербола. 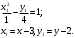 Из найденных уравнений видно, что центр симметрии находится в точке (3,2). Мнимая полуось b=2.Действительная полуось a=1. Уравнение фокальной оси у = 2. 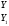 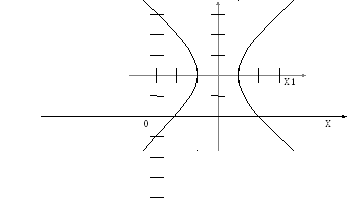 9. Дана кривая y² + 6x + 6y + 15 = 0. 9.1. Докажите, что данная кривая — парабола. 9.2(058.РП). Найдите координаты её вершины. 9.3(2П9). Найдите значения её параметра p. 9.4(289.РП). Запишите уравнение её оси симметрии. 9.5. Постройте данную параболу. Решение: 1.Выделим полные квадраты в уравнении. y²+6y+6x+15=0; (y+3)²-9+6x+15=0; (y+3)²+6x+6=0;  (y+3)²=-6(x+1) - каноническое уравнение параболы. (y+3)²=-6(x+1) - каноническое уравнение параболы.Координаты вершины хº= -1, уº= -3. Найдём значение параметра р: р=-3. Запишем уравнение оси симметрии. у=-3.  10. Дана кривая 5x² + 5y²+ 6xy − 16x − 16y = 16. 10.1. Докажите, что эта кривая — эллипс. 10.2(822.РП). Найдите координаты центра его симметрии. 10.3(470.Б7). Найдите его большую и малую полуоси. 10.4(941.РП). Запишите уравнение фокальной оси. 10.5. Постройте данную кривую. Решение: 1.Приведём уравнение к квадратичной форме: В=5х²+6ху+5у²; Запишем матрицу 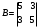 Запишем характеристическое уравнение этой матрицы. 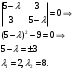 Корни этого уравнения являются собственными числами. Так как λ¹, λ²>0, корни имеют один знак и они не равны, то кривая- эллипс. Для λ¹=2 найдём собственный вектор: 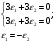 Пусть 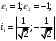 Для 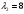 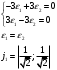 От старого базиса (i, j) перейдём к новому базису (i¹, j¹) 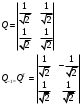 Старые координаты (х, у) связанны с новыми (х¹, у¹) соотношениями  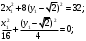 a=4 - большая полуось, b=2 - малая полуось. Произведём преобразование параллельного переноса системы координат в новое начало О¹ 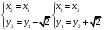 В системе координат (О¹, i, j) эллипс имеет уравнение 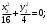 Оси О¹х², О¹у² направлены по прямым х-у =0, х+у-2=0. Координаты точки О¹, являющиеся центром симметрии эллипса, находим, решая систему: х=у х + у=2 О(1;1). | |||||||||||||||||||||
