Найти частное решение дифференциального уравнения первого порядка. Конт раб 3. Контрольная работа 3 Дифференциальные уравнения Задача Найти частное решение дифференциального уравнения первого порядка
 Скачать 59.53 Kb. Скачать 59.53 Kb.
|
|
Контрольная работа № 3 Дифференциальные уравнения Задача 1. Найти частное решение дифференциального уравнения первого порядка. 7. y'ctgx + y=2 y(0)= -1 Решение Решим уравнение ctg(x) 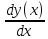 + y(x) = 2 так, чтобы y(0) = -1 + y(x) = 2 так, чтобы y(0) = -1Решим 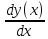 : :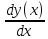 = -(y(x) – 2) tg(x) = -(y(x) – 2) tg(x)Упростим: 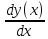 = (-y(x) + 2) tg(x) = (-y(x) + 2) tg(x)Разделим обе стороны –y(x) + 2: 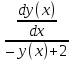 = tg(x) = tg(x)Проинтегрируем обе части 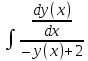 dx = dx =  -log(-y(x)+2) = -log(cos(x)) + 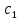 , где , где 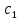 произвольная постоянная произвольная постояннаяРешим y(x): y(x) = - 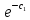 cos(x) + 2 cos(x) + 2Упростим произвольную константу: y(x) = 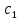 cos(x) + 2 cos(x) + 2Решим 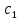 используя начальные условия: используя начальные условия:Заменим y(0) = -1 на y(x) = cos(x) 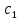 + 2: + 2: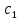 + 2 = -1 + 2 = -1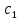 = -3 = -3Заменим 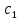 = -3 на y(x) = cos(x) = -3 на y(x) = cos(x)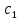 + 2: + 2:y(x) = -3 cos(x) + 2 Задача 2. Найти общее решение дифференциального уравнения высшего порядка, допускающее понижение порядка. 7. y= 2sin5x + 3 Решение Решим  = 2sin5x + 3 = 2sin5x + 3 = = 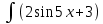 dx = 3x - dx = 3x -  cos5x + cos5x + 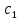 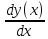 = =  dx = dx =  - - 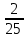 sin5x + sin5x + 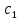 x + + x + + 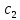 y(x) =  dx = dx = 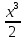 + +  cos5x + cos5x + 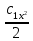 + +  + +  Ответ: y(x) = 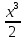 + +  cos5x + cos5x + 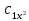 + +  + +  Задача 3. Найти частное решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами со специальной правой частью. 7. y'' + 3y' + 2y = 2 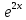 , y(0) = 1, y'(0) = -1 , y(0) = 1, y'(0) = -1Решение Решим  + 3 + 3 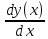 + 2y(x) = 2 + 2y(x) = 2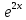 так, чтобы y(0) = 1 и y'(0) = -1 так, чтобы y(0) = 1 и y'(0) = -1Общее решение будет суммой дополнительного решения и частного решения. Найдем дополнительное решение:  + 3 + 3 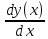 + 2y(x) = 0 + 2y(x) = 0Подставим y(x) = 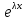 в дифференциальное уравнение: в дифференциальное уравнение: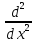 ( ( + 3 + 3  + 2 + 2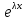 = 0 = 0Заменим 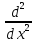 ( ( = =  и и  ( (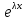 ) = ) =  : : + 3 + 3 + 2 + 2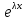 = 0 = 0Исключим 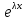 : :( 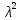 + 3 + 3 + 2) + 2)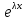 = 0 = 0Поскольку 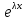 ≠ 0 для любой конечной ≠ 0 для любой конечной  , нули должны происходить от многочлена: , нули должны происходить от многочлена: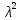 + 3 + 3 + 2 = 0 + 2 = 0(  + 1)( + 1)( + 2) = 0 + 2) = 0Решение для   = -2 или = -2 или  = -1 = -1Корень  = -2 дает = -2 дает  (x) = (x) =  , где , где 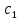 - произвольная постоянная. - произвольная постоянная.Корень  = -1 дает = -1 дает 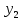 (x) = (x) =  Общее решение это сумма выше перечисленных решений: y(x) =  (x) + (x) + 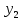 (x) = (x) =  + +  Определим частное решение  + 3 + 3 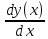 + 2y(x) = 2 + 2y(x) = 2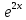 методом неопределенных коэффициентов методом неопределенных коэффициентов (x) = (x) =  Найдем неизвестную константу  : : = =  ( ( ) = 2 ) = 2  = = 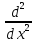 ( ( ) = 4 ) = 4  Подставим частное решение  (x) в дифференциальное уравнение: (x) в дифференциальное уравнение: + 3 + 3 + 2 + 2 (x) = 2 (x) = 2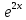 4  + 3(2 + 3(2 ) + 2( ) + 2( ) = 2 ) = 2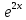 Упростим: 12  = 2 = 2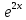 Приравняем коэффициенты 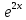 в обеих частях уравнения: в обеих частях уравнения:12  = 2 = 2 = =  Заменим  на на  (x) = (x) =  : : (x) = (x) =  y(x) =  (x) + (x) +  (x) = (x) =  + +  + +  Решим неизвестную константу, используя начальные условия 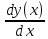 = =  ( (  + +  + +  ) = ) = 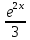 - 2 - 2 - -  Заменим y(0) = 1 на y(x) =  + +  + +  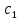 + + 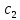 + +  = 1 = 1Заменим y'(0) = -1 на 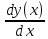 = = 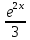 - 2 - 2 - -  -2 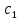 - - 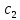 + +  = -1 = -1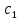 = = 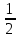 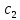 = =  Заменим 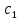 = = 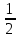 и и 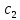 = =  на y(x) = на y(x) =  + +  + +  y(x) =  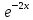 ( (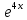 + +  + 3) + 3)Ответ: y(x) =  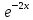 ( (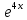 + +  + 3) + 3)Задача 4. Изменить порядок интегрирования в двойном интеграле. Сделать чертѐж области интегрирования   Построим область интегрирования ограниченную кривыми 0≤y≤4, 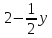 ≤x≤ ≤x≤ , где , где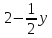 - парабола с вершиной в точке O(0;0) и ветками вверх; - парабола с вершиной в точке O(0;0) и ветками вверх; - прямая, которая проходит через начало координат O(0;0). - прямая, которая проходит через начало координат O(0;0). x= 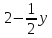 - -  x= 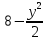 Найдем точки перечения: x= 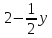 = =   = 0 ; = 0 ; 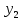 = 4 = 4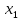 = 0; = 0; 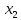 = 32 - = 32 -  Расставим пределы в заданной области: D: 0≤ x ≤ 32 -  , , 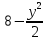 ≤ y ≤ ≤ y ≤  Выполняем изменение порядка интегрирования   = = 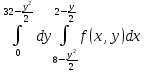 |
