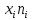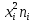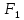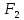Эконометрика кр. эконометрика кр. Контрольная работа по дисциплине Эконометрика
 Скачать 33.78 Kb. Скачать 33.78 Kb.
|
|
Федеральное государственное автономное образовательное учреждение высшего образования «Российский университет транспорта (МИИТ)» (РУТ (МИИТ) Российская открытая академия транспорта Кафедра «Высшая математика и естественные науки» КОНТРОЛЬНАЯ РАБОТА по дисциплине: Эконометрика Вариант № 8
Москва 2023 г. Задача 1.Дано статистическое распределение выборки, где 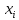 – результаты измерений, – результаты измерений, 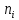 – частоты. Найти: а) выборочную среднюю; б) выборочную дисперсию; в) исправленную выборочную дисперсию; г) выборочное среднее квадратическое отклонение; д) исправленное среднее квадратическое отклонение. Построить гистограмму частот. – частоты. Найти: а) выборочную среднюю; б) выборочную дисперсию; в) исправленную выборочную дисперсию; г) выборочное среднее квадратическое отклонение; д) исправленное среднее квадратическое отклонение. Построить гистограмму частот.
Решение.Промежуточные расчеты приведем в таблице:
а) Выборочная средняя: 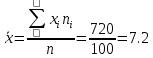 б) Выборочная дисперсия: 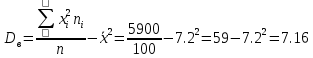 в) Исправленная выборочная дисперсия: 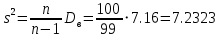 г) Выборочное среднее квадратическое отклонение: 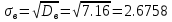 д) Исправленное среднее квадратическое отклонение: 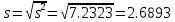 Построим гистограмму частот. 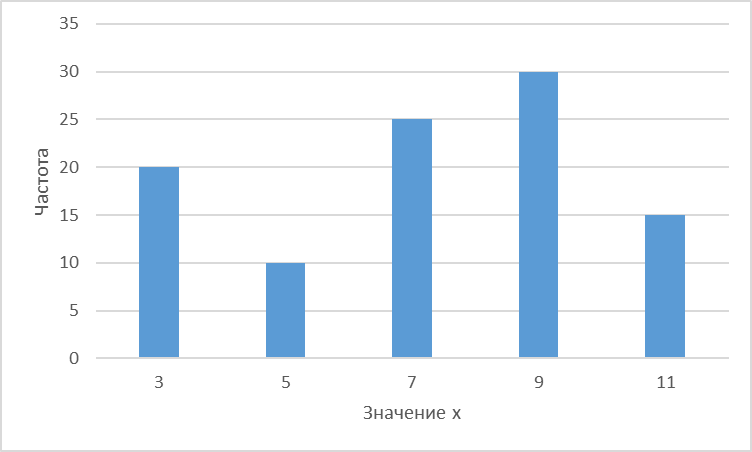 Ответ.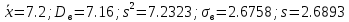 . .Задача 2.Ежемесячный объем выпуска продукции завода является случайной величиной, распределенной по показательному закону. Имеются данные об объеме выпуска в течение шести месяцев. Методом моментов найти точечную оценку параметра распределения.
Решение.Найдем методом моментов точечную оценку параметра 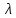 показательного распределения. Приравняем начальные эмпирический и теоретический моменты: показательного распределения. Приравняем начальные эмпирический и теоретический моменты: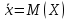 Так как для показательного распределения 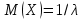 , уравнение примет вид , уравнение примет вид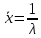 Решая уравнение относительно неизвестного параметра, получим оценку методом моментов: 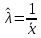 По заданной выборке вычислим значение полученной оценки: 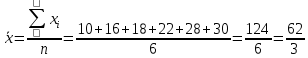 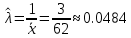 Ответ.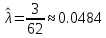 . .Задача 3.Найти доверительный интервал для оценки математического ожидания 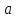 нормального распределения с надежностью 0,95, зная выборочную среднюю нормального распределения с надежностью 0,95, зная выборочную среднюю 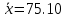 , объем выборки , объем выборки 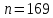 и среднее квадратическое отклонение и среднее квадратическое отклонение 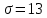 . В ходе решения задачи использовать Приложение 1. . В ходе решения задачи использовать Приложение 1.Решение.При известном генеральном среднем квадратическом отклонении доверительный интервал для оценки математического ожидания 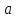 нормального распределения имеет вид нормального распределения имеет вид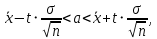 где 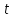 находится из таблицы значений функции Лапласа (Приложение 1) по равенству находится из таблицы значений функции Лапласа (Приложение 1) по равенству 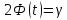 , , 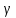 – заданная надежность. – заданная надежность. 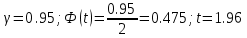 Получим: 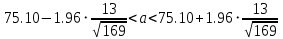 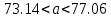 Ответ.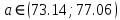 . .Задача 4.Для проверки эффективности новой технологии отобраны две группы рабочих численностью 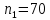 и и 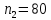 человек. В первой группе, где применялась новая технология, выборочная средняя выработки составила человек. В первой группе, где применялась новая технология, выборочная средняя выработки составила 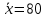 изделий, во второй - изделий, во второй - 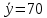 изделий. Установлено, что дисперсии выработки в группах равны соответственно изделий. Установлено, что дисперсии выработки в группах равны соответственно 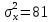 и и 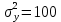 . .Требуется на уровне значимости 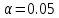 выяснить влияние новой технологии на среднюю производительность. выяснить влияние новой технологии на среднюю производительность.Решение.Судя по обозначениям, заданы генеральные дисперсии. Проверим гипотезу 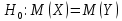 при альтернативной гипотезе при альтернативной гипотезе 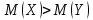 . .Вычислим наблюдаемое значение критерия: 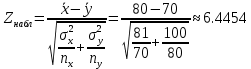 По таблице значений функции Лапласа (Приложение 1) по уровню значимости 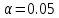 найдем критическую точку правосторонней критической области: найдем критическую точку правосторонней критической области: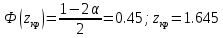 Так как 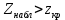 , нулевую гипотезу следует отвергнуть. На заданном уровне значимости можно утверждать, что новая технология статистически значимо повышает среднюю производительность. , нулевую гипотезу следует отвергнуть. На заданном уровне значимости можно утверждать, что новая технология статистически значимо повышает среднюю производительность. Ответ. На заданном уровне значимости можно утверждать, что новая технология статистически значимо повышает среднюю производительность. Задача 5.Для проверки влияния технологии на качество однотипной продукции проведена выборочная проверка процента брака за пять месяцев на трех производственных участках. Результаты проверки представлены в таблице (матрице наблюдений). Методом однофакторного дисперсионного анализа при уровне значимости 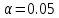 проверить нулевую гипотезу о существенном влиянии технологии на качество продукции. В ходе решения задачи использовать Приложение 2. проверить нулевую гипотезу о существенном влиянии технологии на качество продукции. В ходе решения задачи использовать Приложение 2.
Решение.На уровне значимости 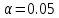 проверим нулевую гипотезу о равенстве групповых средних при допущении, что групповые генеральные дисперсии хотя и неизвестны, но одинаковы. проверим нулевую гипотезу о равенстве групповых средних при допущении, что групповые генеральные дисперсии хотя и неизвестны, но одинаковы. Найдем групповые средние: 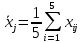 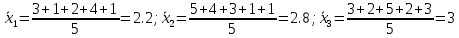 Общая средняя: 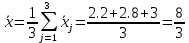 Найдем общую сумму квадратов отклонений наблюдаемых значений признака от общей средней: 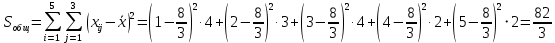 Найдем факторную сумму квадратов отклонений групповых средних от общей средней (характеризует рассеяние «между группами»): 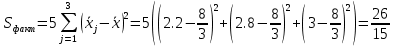 Найдем остаточную сумму квадратов отклонений наблюдаемых значений группы от своей групповой средней (характеризует рассеяние «внутри групп») 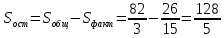 Найдем факторную и остаточную дисперсии: 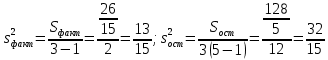 Сравним факторную и остаточную дисперсии с помощью критерия Фишера-Снедекора. Наблюдаемое значение критерия: 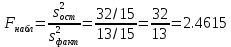 В таблице критических точек распределения Фишера-Снедекора (Приложение 2) по уровню значимости 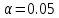 и числам степеней свободы и числам степеней свободы 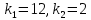 найдем критическую точку: найдем критическую точку: 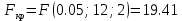 . .Так как 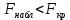 , нет оснований отвергнуть нулевую гипотезу о равенстве групповых средних. Другими словами, групповые средние различаются статистически незначимо, то есть влияние технологии на качество продукции несущественно. , нет оснований отвергнуть нулевую гипотезу о равенстве групповых средних. Другими словами, групповые средние различаются статистически незначимо, то есть влияние технологии на качество продукции несущественно.Ответ. На заданном уровне значимости можно утверждать, что влияние технологии на качество продукции несущественно. Задача 6.Выборочная зависимость между величиной основных производственных фондов 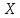 и суточной выработкой продукции и суточной выработкой продукции 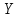 по данным пяти независимых наблюдений представлена в таблице. по данным пяти независимых наблюдений представлена в таблице.Требуется составить выборочное уравнение линейной парной регрессии 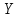 на на 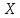 , вычислить коэффициент корреляции , вычислить коэффициент корреляции 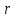 между между 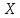 и и 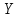 , на уровне значимости , на уровне значимости 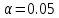 проверить значимость коэффициента корреляции и уравнения регрессии. проверить значимость коэффициента корреляции и уравнения регрессии.
Решение.Найдем выборочные характеристики:
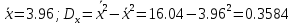 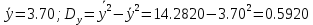 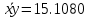 Составим уравнение регрессии 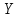 на на 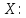 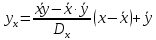 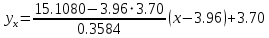 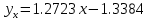 Вычислим коэффициент корреляции 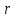 между между 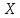 и и 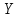 : :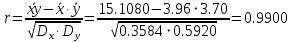 Проверим значимость коэффициента корреляции, то есть проверим гипотезу 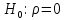 при альтернативной гипотезе при альтернативной гипотезе 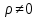 . .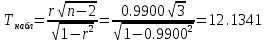 По таблице критических точек распределения Стьюдента по уровню значимости 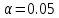 и числу степеней свободы и числу степеней свободы 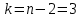 найдем критическую точку двусторонней критической области: найдем критическую точку двусторонней критической области: 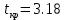 . Так как . Так как 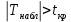 , нулевую гипотезу следует отвергнуть, то есть выборочный коэффициент корреляции статистически значим. , нулевую гипотезу следует отвергнуть, то есть выборочный коэффициент корреляции статистически значим.Проверим значимость уравнения регрессии в целом. В случае линейной парной регрессии наблюдаемое значение критерия: 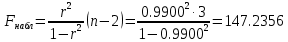 По таблице критических точек распределения Фишера-Снедекора (Приложение 2) по 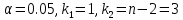 найдем найдем 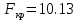 . Так как . Так как 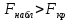 , то на заданном уровне значимости можно утверждать, что полученное уравнение регрессии статистически значимо. , то на заданном уровне значимости можно утверждать, что полученное уравнение регрессии статистически значимо.Ответ. 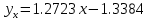 ; выборочное уравнение регрессии статистически значимо; ; выборочное уравнение регрессии статистически значимо; 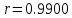 ; выборочный коэффициент корреляции статистически значим. ; выборочный коэффициент корреляции статистически значим.Задача 7.В таблице приведены данные, отражающие спрос на некоторый товар за семилетний период (усл. ед.). Найти уравнение тренда для временного ряда, полагая тренд линейным.
Решение.Искомое уравнение тренда имеет вид 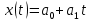 , где коэффициенты , где коэффициенты 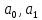 находятся из системы уравнений находятся из системы уравнений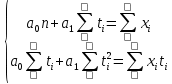 Найдем суммы: 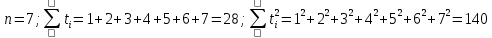 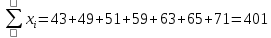 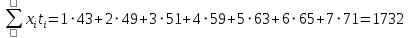 Составим систему: 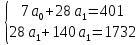 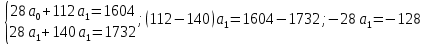 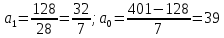 Итак, искомое уравнение тренда: 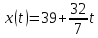 Ответ. 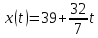 . . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||