метрология. Работа. Контрольная работа проверка согласия опытного распределения с теортическим по дисциплине Метрология

• Название: Контрольная работа проверка согласия опытного распределения с теортическим по дисциплине Метрология
• Анкор: метрология
• Дата: 21.01.2023
• Размер: 50.66 Kb.
• Имя файла: Работа.docx
• Тип: Контрольная работа; #897828

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ

КАФЕДРА №6

ОЦЕНКА

ПРЕПОДАВАТЕЛЬ

доц., канд. техн. наук				Скорнякова Е.А.
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

КОНТРОЛЬНАЯ РАБОТА

ПРОВЕРКА СОГЛАСИЯ ОПЫТНОГО РАСПРЕДЕЛЕНИЯ С ТЕОРТИЧЕСКИМ

по дисциплине: «Метрология»

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №
	номер группы		подпись, дата		инициалы, фамилия
Студенческий билет №

Санкт-Петербург 2023

Оглавление

1. Перечень применяемых НД 3

2. Цель работы 3

3. Постановка задачи 3

4. Номер и исходные данные варианта 4

5. Результаты выполнения действий по п.4 методических указаний 4

Выводы 7

1. Перечень применяемых НД

1. Р 50.1.033-2001. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть I. Критерии типа «хи-квадрат».

2. Р 50.1.037-2002. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть II. Непараметрические критерии.

3. Р 50.1.072-2010. Статистические методы. Примеры применения. Часть 1. Группировка данных.

4. Р 50.1.082-2012. Статистические методы. Примеры применения. Часть 4. Простые статистические методы анализа данных.

5. Р 50.1.086-2013. Статистические методы. Примеры применения. Часть 6. Анализ выборочных оценок среднего и СКО.

2. Цель работы

Цель – ознакомление и приобретение первичных навыков по применению параметрических методов проверки согласия опытного распределения измеренных значений величины с теоретическим.

3. Постановка задачи

Проверить соответствие опытного распределения измеренных значений величины у, определяемой по уравнению: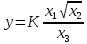

(1)

теоретическому при заданных значениях входных величин x₁, x₂, x₃ и известных параметрах и законах их распределений.

4. Номер и исходные данные варианта

Вариант 12

№ варианта

Константа, K

x1

x2

x3

Параметры распределения

Параметры распределения

Параметры распределения

M(x)=а

D(x)

σ

M(x)=a

D(x)

σ

M(x)

b

σ

Нормальное

Нормальное

Равномерное

12

0,0776

1,66

=σ2

0,17

15,66

=σ2

0,57

0,045

0,050

=(b-с)/121/2

5. Результаты выполнения действий по п.4 методических указаний

Создадим с помощью генератора случайных чисел три массива для х₁, х₂, х₃ из 300 чисел каждый, поместив их в соседние столбцы таблицы Excel.

В следующем столбце поместим результаты расчетов по формуле (1) для выходной величины у.

В следующем столбце расположим числа массива значений у в порядке возрастания.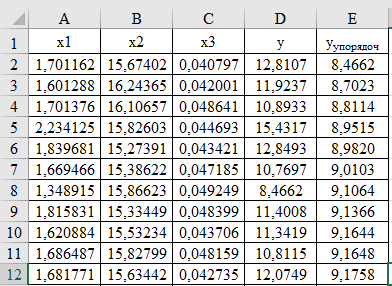



Рис. 1 Фрагмент таблицы
Вычислим параметры массива значений у (описательная статистика в Excel) – среднее арифметическое (математическое ожидание М(х) или параметр сдвига θ₀) и СКО распределения (σ или параметр масштаба θ₁).

Среднее	СКО	max	min
11,4139	1,3316	15,4317	8,4662

Определим оптимальное число интервалов группирования по рекомендациям из таблицы 1 методических указаний для n = 300 возьмем k = 8.

Определим значения граничных точек асимптотически оптимального группирования t_i, инвариантных к параметрам распределения, по таблице А.28 (приложение А).

8

-2,1954

-1,4552

-0,7863

0

0,7863

1,4552

2,1954

Определим значения границ интервалов x_i по формуле: t_i=(x_i – θ₀)/θ₁.

8,4904

9,4761

10,3668

11,4139

12,4610

13,3517

14,3374

Определим теоретические вероятности попадания наблюдений в интервалы по табл. А.29 (приложение А).

0,0141

0,0587

0,1431

0,2841

0,2841

0,1431

0,0587

0,0141

По упорядоченной выборке у определим число точек n_i, попадающих в интервалы группирования.

№ интервала	Левая граница	Правая граница	Число попаданий
1	8,0000	8,4904	1
2	8,4904	9,4761	18
3	9,4761	10,3668	54
4	10,3668	11,4139	87
5	11,4139	12,4610	77
6	12,4610	13,3517	40
7	13,3517	14,3374	16
8	14,3374	15,5000	7
Сумма			300

По формуле (1) вычислим статистику критерия согласия χ² Пирсона Sχ².

№ интервала	Левая граница	Правая граница	Число попаданий	Относительное число попаданий	Теоретическая частота	(ni/N-Pi)2/Pi
1	8,0000	8,4904	1	0,0033	0,0141	0,00822
2	8,4904	9,4761	18	0,0600	0,0587	0,00003
3	9,4761	10,3668	54	0,1800	0,1431	0,00952
4	10,3668	11,4139	87	0,2900	0,2841	0,00012
5	11,4139	12,4610	77	0,2567	0,2841	0,00265
6	12,4610	13,3517	40	0,1333	0,1431	0,00067
7	13,3517	14,3374	16	0,0533	0,0587	0,00049
8	14,3374	15,5000	7	0,0233	0,0141	0,00605
Сумма			300	1	1	0,02774

Sχ² = 0,02774*300 = 8,322
Сравним вычисленную статистику с критическими значениями теоретического распределения χ_r², с числом степеней свободы r = k–m–1 (табл. приложения Б 1). В нашем случае: r = k–3 = 8 -3 = 5

Исходя из выполнения неравенства: P{S_χ² > S_α} > α определим значение уровня значимости α, при котором гипотеза Н₀ о соответствии опытного распределения теоретическому принимается.

P{S_χ² > 8,322} = 0,139

При значениях уровня значимости α > 0,139 гипотеза H₀ будет отклонена.

Построить гистограмму и график теоретического распределения.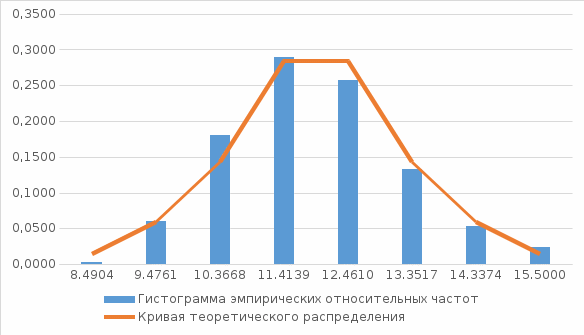



Рис. 2 Гистограмма и график теоретического распределения

Выводы

В результате проверки согласия опытного распределения измеренных значений величины с теоретическим было получены параметры распределения измеренных значений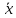

= 11,414 σ=1,332

Рассчитана статистика критерия согласия χ² Пирсона Sχ² = 8,322.

Проверена гипотеза Н₀ о соответствии опытного распределения теоретическому нормальному распределению с параметрами 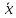, σ.

При значениях уровня значимости α ≤ 0,139 гипотеза H₀ принимается.

При значениях уровня значимости α > 0,139 гипотеза H₀ будет отклонена.