КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие параметры сигнала могут быть измерены с помощью осциллографа?
2. Какая связь существует между временным и частотным представлением сигналов (если такая связь существует)?
3. Какие параметры сигнала могут быть измерены с помощью анализатора спектра?
4. Что представляет собой спектр периодического сигнала? Укажите основные признаки.
5. Из каких компонент состоит спектр периодической последовательности прямоугольных импульсов?
6. В каких соотношениях между собой находятся спектр сигнала и частотная характеристика линии связи? Что происходит при нарушении этого
соотношения?
7. Что такое оценка сигнала? Укажите основные параметры оценки сигнала.
8. Как связаны мощность сигнала и мощность оценки сигнала? Приведите количественные соотношения.
9. Что такое эффективная длительность сигнала? Как можно определить
эффективную длительность сигнала?
10. Что такое пороговая длительность сигнала? Как можно определить
пороговую длительность сигнала?
11. Что такое эффективная ширина спектра сигнала? Как можно определить эффективную ширину спектра сигнала?
12. Как с помощью маркеров на временной диаграмме можно определить
частоту (амплитуду) гармонического колебания?
13. Как на графике АЧХ спектра определить ширину спектра сигнала по
пороговому критерию?
14. Что такое прямое преобразование Фурье? Приведите необходимые
пояснения.
15. Что такое прямое преобразование Фурье? Приведите необходимые
пояснения.
16. Что понимается под ортогональной системой базисных функций?
Дайте пояснения по каждому признаку.
17. Какая ортогональная система базисных функций называется полной?
Укажите признаки полноты.
18. Какая система базисных функций называется ортонормированной?
Укажите условия нормировки.
Какие параметры сигнала могут быть измерены с помощью осциллографа?
Осциллограф – прибор, показывающий форму напряжения во времени. Также он позволяет измерять ряд параметров сигнала, такие как напряжение, ток, частота, угол сдвига фаз. Но главная польза от осциллографа – возможность наблюдения формы сигнала. Во многих случаях именно форма сигнала позволяет определить, что именно происходит в цепи.
В основе всех видов измерений современного осциллографа лежат два вида измерений – это амплитудные и временные. Так же цифровые осциллографы способны осуществлять безразмерные виды измерений, например подсчет числа целых периодов сигнала, числа точек дискретизации, числа пиков гистограммы и пр. Амплитудные измерения предназначены для измерений параметров амплитуды входного сигнала (или же результатов математической обработки) – это такие как, непосредственно, амплитуда, нижнее значение, верхнее значение, пиков значение, выбросы, среднеквадратическое значение и многие другие. Временные измерения предназначены для измерений параметров сигнала нормированных по времени – это частота, период, длительность, фазовые сдвиги, время нарастания и спада, параметры джиттера и многие другие. Так же современные ЦЗО (цифровые запоминающие осциллограф) имеют некоторые производные виды измерений от амплитуды и времени, например измерение площади сигнала, что применительно к импульсному сигналу определяет его энергию, измерение числа периодов сигнала на заданном участке или измерение числа точек дискретизации образующих форму сигнала на всем экране или на заданном участке. В ЦЗО так же присутствуют специализированные виды измерений, предназначенные для измерения параметров специфических устройств или режимов, например измерение параметров мощности электрического сигнала, измерение параметров систем последовательной передачи данных, измерение параметров дисковых или оптических приводов, измерения джиттера и многие другие. Но и даже эти специализированные виды измерений базируются на основных результатах измерения амплитудно-временных параметров сигнала.
2. Какая связь существует между временным и частотным представлением сигналов (если такая связь существует)?
Электрические сигналы можно исследовать во временной области с помощью осциллографа и в частотной области с помощью анализатора спектра. Эти два режима отображения сигналов связаны друг с другом преобразованием Фурье (обозначается как F), поэтому каждый сигнал во временной области имеет характерный частотный спектр. Согласно теореме Фурье любой сигнал, являющийся периодическим во временной области, может быть получен из суммы синусоидальных и косинусоидальных сигналов разной частоты и амплитуды. Такая сумма называется рядом Фурье. Спектральный анализ - один из методов обработки сигналов, который позволяет охарактеризовать частотный состав измеряемого сигнала. Преобразование Фурье является математической основой, которая связывает временной или пространственный сигнал (или же некоторую модель этого сигнала) с его представлением в частотной области
3. Какие параметры сигнала могут быть измерены с помощью анализатора спектра?
Анализатор спектра – это устройство, позволяющее измерить и визуализировать спектр сигнала. Сам спектр сигнала представляет собой набор синусоидальных волн в определенный момент времени и отображает распределение энергии сигнала по частотам. Анализатор спектра выдает частотно-амплитудную характеристику сигнала.
Назначение
Анализатор спектра подает сигнал в частотной форме. Таким образом, становится возможным проанализировать сигнал с точки зрения его частоты, амплитуды и уровней.
Этот прибор является важным инструментом при разработке, обслуживании и эксплуатации радиоаппаратуры, мобильного и телекоммуникационного оборудования, а также самых разных систем связи. Кроме того, анализаторы спектра применяются для редактирования и реставрирования звука.
Типы измерений Чаще всего с помощью анализаторов спектра измеряют частоту, мощность, модуляцию, искажения и шум. Знание спектрального состава сигнала очень важно, особенно в системах с полосой частот ограниченной ширины. Переданная мощность также является важным измеряемым параметром. Слишком малая мощность означает, что сигнал не сможет достичь точки назначения. Слишком большая мощность может быстро истощить заряд батарей, создать искажения и чрезмерно повысить рабочую температуру системы. Измерение качества модуляции может быть важным для того, чтобы обеспечить нормальную работу системы и быть уверенным в том, что информация передается корректно. Измерения коэффициента модуляции, амплитуды боковых полос (частот), качества модуляции и заполнения полосы частот – это примеры самых распространенных измерений при аналоговой модуляции. В случае цифровой модуляции измеряются модуль вектора погрешности, дисбаланс IQ, зависимость неопределенности фазы от времени и ряд других параметров. Более подробно об этих видах измерений рассказано в документе Agilent Application Note 150-15, Vector Signal Analysis Basics. В сфере коммуникаций и связи измерение искажений очень важно как для приемников, так и для передатчиков. Излишние гармонические искажения на выходе передатчика могут создавать помехи на других коммуникационных частотах. В блоках предусилителей приемника не должно быть интермодуляции, чтобы избежать перекрестного наложения сигнала. Хороший пример – интермодуляция несущих сигналов кабельного телевидения, которые при распространении по распределительной системе вносят искажения в другие каналы этого же кабеля. Распространенными измерениями искажений являются измерения интермодуляции, гармоник и паразитного излучения. Часто бывает нужно измерить и шум как сигнал. Любая активная цепь или устройство будет генерировать шум. Измерения коэффициента шума и отношения сигнал/шум (С/Ш) являются важными для описания показателей устройства и его вклада в общие показатели системы.
4. Что представляет собой спектр периодического сигнала? Укажите основные признаки.
В теории и практике радиотехники и радиоэлектроники часто встречаются процессы, которые могут рассматриваться как периодические. Периодическим сигналом (током или напряжением) называют такой вид воздействия, когда форма сигнала повторяется через некоторый интервал времени T, который называется периодом. Периодический сигнал описывает бесконечно повторяющийся во времени физический процесс и является полезной абстракцией, используемой при решении практических задач. Простейшей формой периодического сигнала является гармонический сигнал или синусоида, которая характеризуется амплитудой, периодом и начальной фазой. Под гармоническим анализом понимают разложение периодического сигнала на сумму гармоник с частотами, кратными основной частоте повторения периодической последовательности. 3. Суммирование гармоник с определенными амплитудами и начальными фазами позволяет восстановить периодический сигнал с любой заданной точностью. 4. Под спектральными характеристиками периодического сигнала понимают распределение амплитуд (и начальных фаз) по частотам, их называют спектрами амплитуд и фаз соответственно. 5. Временное и спектральное представления однозначно описывают периодический сигнал в двух разных плоскостях: мгновенное значение – время и амплитуда – частота (начальная фаза – частота). 6. Временное представление периодического сигнала, как правило, аналоговая функция времени. Спектральное представление периодического сигнала – дискретная затухающая функция частоты. 7. Экспериментальное исследование временного представления осуществляется с помощью осциллографа, поэтому s t( ) называют осциллограммой. Экспериментальное исследование спектрального представления выполняется с помощью анализатора спектра и называется спектрограммой. 8. Форма периодического сигнала определяет поведение спектра амплитуд и распределение начальных фаз гармоник. Если начальные фазы гармоник 0 либо π, то периодический сигнал обладает четной симметрией относительно начала координат. Если начальные фазы гармоник ±π 2, то периодический сигнал обладает нечетной симметрией относительно начала координат. Если спектр амплитуд затухает медленно, то периодический сигнал имеет разрывы. Если в спектре амплитуд «исчезают» некоторые гармоники (или огибающая спектра амплитуд пульсирует), то это признак импульсного характера периодического сигнала. 9. Мощность периодического сигнала сложной формы равна сумме мощностей отдельных гармонических составляющих. Среднеквадратическое значение погрешности представления периодического сигнала конечной суммой гармоник равно разности мощностей сигнала и оценки.
5. Из каких компонент состоит спектр периодической последовательности прямоугольных импульсов? (стр 53 в учебнике)
Рассмотрим периодическую последовательность прямоугольных импульсов, изображенную на рис. 5. Данный сигнал характеризуется длительностью импульса, его амплитудой и периодом.

ачало отсчета выберем в середине импульса. Тогда сигнал разлагается только по косинусам. Частоты гармоник равны n/T , где n - любое целое число. Амплитуды гармоник согласно (1.2.) будут равны:
 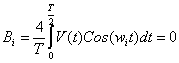
так как V(t)=Е при 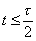 , где , где 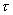 - длительности импульса и V(t)=0 при - длительности импульса и V(t)=0 при 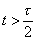 , то , то
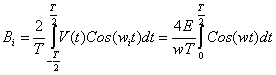
Эту формулу удобно записать в виде:
 (2.1.) (2.1.)
Формула (1.5.) дает зависимость амплитуды n-ой гармоники от периода и длительности в виде непрерывной функции (функция 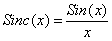 ). Эту функцию называют огибающей спектра. Следует иметь ввиду, что физический смысл она имеет только на частотах, где существуют соответствующие гармоники. На рис. 6 приведен спектр периодической последовательности прямоугольных импульсов. ). Эту функцию называют огибающей спектра. Следует иметь ввиду, что физический смысл она имеет только на частотах, где существуют соответствующие гармоники. На рис. 6 приведен спектр периодической последовательности прямоугольных импульсов.

Рис.6. Спектр периодической последовательности
прямоугольных импульсов.
При построении огибающей имеем ввиду, что 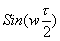 - является - является
осцилирующей функцией частоты, а знаменатель монотонно возрастает с ростом частоты. Поэтому получается квазиосцилирующая функция с постепенным убыванием. При частоте стремящейся к нулю, к нулю стремятся одновременно и числитель и знаменатель, их отношение стремится к единице (первый классический предел). Нулевые значения огибающей возникают в точках где 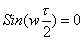 т. е. т. е.
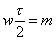
, где m – целое число (кроме m=0). Переходя от циклической частоты к частоте в Гц, получаем:
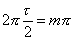 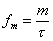 (2.2.) (2.2.)
Эти значения отмечены на рис. 6.
Огибающая ограничивает на графике амплитуды гармоник. Форма огибающей определяется формой и длительностью импульса, а частоты гармоник только его периодом /2/. Это утверждение, полученное для прямоугольных импульсов справедливо и для других периодических сигналов.
6. В каких соотношениях между собой находятся спектр сигнала и частотная характеристика линии связи? Что происходит при нарушении этого соотношения?
. Обычно частотные характеристики называют частотными спектрами, или спектрами, сигнала. Принято и другое название – спектральные характеристики
С помощью спектральных характеристик оценивают внутренний состав (спектр) сигнала. Для этого сигнал x(t) представляют в форме обобщенного ряда Фурье, раскладывая его по системе базисных функций Тk(t)

где Ск — постоянные коэффициенты, отражающие вклад функции Ч^(?) в формирование значений сигнала на рассматриваемом промежутке времени.
Возможность представления сложного сигнала x(t) в виде суммы простых сигналов 'РДО оказывается особенно важной для линейных динамических систем. В таких системах выполняется принцип суперпозиции, т.е. их реакция на сумму воздействий (сигналов) равна сумме реакций на каждое из воздействий в отдельности. Поэтому, зная реакцию линейной системы на простой сигнал, можно, суммируя результаты, определить ее реакцию на любой другой сложный сигнал.
Выбор функций Уk(t) подчиняют требованиям максимальной точности приближения сигнала х(t) рядом (7.21) при минимальном числе членов этого ряда и, по возможности, снижению вычислительных трудностей, возникающих при определении коэффициентов ряда Ск.
В качестве базисных функций наиболее широкое применение получили вещественные тригонометрические функции
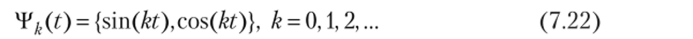
и комплексные экспоненциальные функции
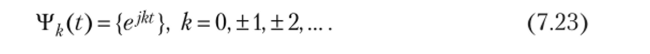
На них строится классический спектральный анализ сигналов. Вместе с тем возможно применение других систем базисных функций (функций Тейлора, Уолша, Лагерра, Эрмита, Лежандра, Чебышева, Котельникова и др. 121), что в ряде случаев позволяет, учитывая специфику приближаемой функции x(t), сократить число членов ряда (7.21) при сохранении заданной погрешности приближения.
В последние годы появилась новая, весьма перспективная система базисных функций, называемых вейвлетами. В отличие от гармонических функций, они способны, изменяя свою форму и свойства, адаптироваться к локальным особенностям приближаемого сигнала. В результате становится возможным простое представление сложных сигналов (в том числе с локальными скачками и разрывами) наборами вейвлетов того или иного типа [2].
При использовании тригонометрических базисных функций (7.22), ряд (7.21) приобретает форму классического тригонометрического ряда Фурье
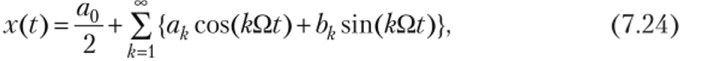
где Q = 2п/Т — частота основной гармоники ряда (Г — период сигнала); к = 1, 2, 3,... — целое число; ak, bk — действительные числа (коэффициенты Фурье), вычисляемые но формулам

В этих формулах, как и прежде (см. (7.20)), t0 — произвольное число, которое можно выбирать из соображений удобства вычисления интегралов (7.25), так как значения этих интегралов от величины t0 не зависят; xT(t) — базовый импульс сигнала (см. рис. 7.3, в).
Коэффициент а0 определяет удвоенное среднее (за период) значение сигнала, остальные коэффициенты ak> bk {k = 1, 2, 3, ...) — вклад к-й гармоники ряда Фурье (7.24) в формирование мгновенных значений сигнала х(?).
Тригонометрический ряд Фурье (7.24) можно записать в двух других формах: в форме разложения по синусам
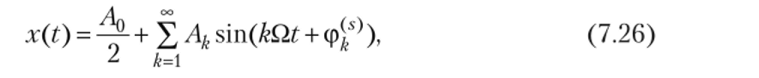
и в форме разложения по косинусам 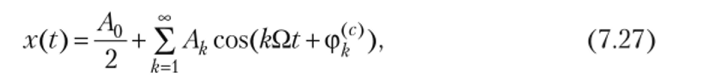
где Л0/2 = а0/2 — постоянная составляющая сигнала; Ak — амплитуда k-и гармоники ряда, вычисляемая по формуле

Начальные фазы этих гармоник вычисляются из соотношений
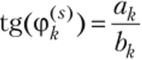
или

Совокупность амплитуд гармонических составляющих периодического сигнала {Ак}°?={ называется амплитудным спектром этого сигнала. Совокупность начальных фаз этих составляющих {ф/^}^=1 — фазовым спектром сигнала.
Используя 5-функцию Дирака 8(?), оба спектра можно представить решетчатыми функциями частоты

т.с. амплитудный и фазовый спектры периодического сигнала являются дискретными спектрами. Это отличает периодический сигнал от других сигналов, обладающих сплошными спектрами.
Таким образом, периодический сигнал можно представить в виде суммы гармоник (7.24). При этом частота каждой гармонической составляющей ряда Фурье кратна частоте основной гармоники ?2, зависящей от периода сигнала Т.
Чем больше таких гармоник, тем меньше погрешность приближения функции x(t) конечной суммой ряда Фурье (7.24). Исключением являются точки разрыва непрерывности функции x(i). В окрестности таких точек проявляется так называемое явление Гиббса |2|. Согласно этому явлению в окрестностях точек разрыва конечные суммы ряда Фурье
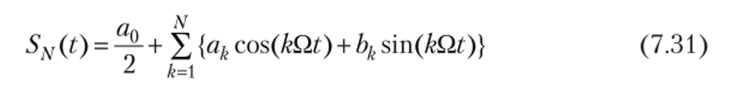
образуют осциллирующие «хвосты», высота которых не уменьшается с ростом числа учитываемых гармоник ряда Фурье N — она составляет примерно 9% от величины скачка функции x{t) в точке разрыва.
Для вычисления амплитуды и начальной фазы &-й гармоники периодического сигнала можно вместо формул (7.28) и (7.29) использовать формулы 
где Хт = Хт(р) = L{xT(t)} индекс Тпеременной х — изображение по Лапласу базового импульса сигнала, определяемое по формуле (см. приложение 2)

i — мнимая единица; & = 0,1,2,... — положительное целое число. Использование этих формул исключает необходимость вычисления интегралов (7.25), что значительно упрощает расчеты. Покажем пример такого расчета.
Пример 7.1

Определить амплитудный спектр периодического сигнала Решение
На рис. 7.3, а, показан график такого сигнала. Видно, что сигнал имеет период Т = я. Следовательно, частота основной гармоники соответствующего ряда Фурье (7.24) равна Q = 2п/Т = 2 с-1. Принимая t0 = 0, xT(t) = sin? (для 0 < t < я), но формулам (7.25) вычислим коэффициенты Фурье:
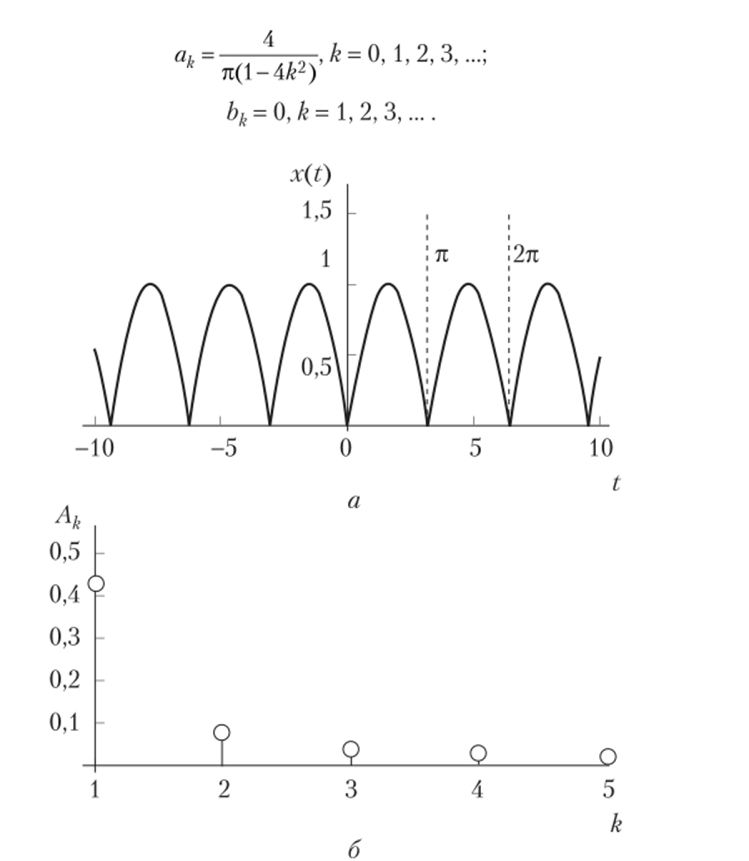
Рис. 73. Результаты спектрального анализа сигнала ,r(l) = |sin(f)|:
а — форма сигнала; б — амплитудный спектр сигнала
Следовательно, А0/2 = 2/п, Ak = 4/я(4&2 - 1), щ = л, где k = 1,2, 3,т.е. разложение функции |sin(?)| в тригонометрический ряд Фурье имеет вид
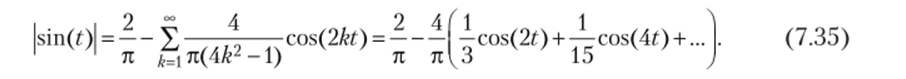
Примечание: здесь принято ф/, = л (а нс ук = 0) из-за использования знака «минус» перед суммой гармоник ряда.
На рис. 7.3, б показан амплитудный спектр рассматриваемого сигнала. Значение амплитуды ?-й гармоники ряда Ак представлено вертикальным отрезком соответствующей длины, в основании которого указан номер гармоники.
Следует иметь в виду, что амплитуды Ак некоторых гармоник ряда Фурье могут быть равны нулю. Кроме того, необязательным является монотонное уменьшение амплитуд этих гармоник с ростом номера гармоники, как это имеет место на рис. 7.3, б.
Однако во всех случаях должно выполняться условие lim Ак = 0, вытекающее из тре-
к—
бования сходимости ряда Фурье.
Решим задачу с использованием формул (7.32). Для этого сначала найдем изображение по Лапласу базового импульса сигнала xT(t)
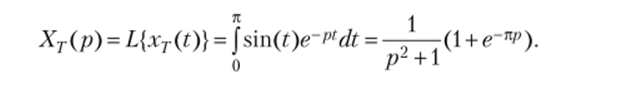
Подставляя сюда p = ikQ = 2ik (где i — мнимая единица, k = 1, 2, 3,...), получим 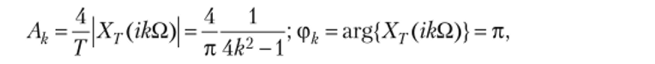 что совпадает с прежними результатами. что совпадает с прежними результатами.
В технических приложениях часто пользуются комплексной формой записи ряда Фурье

В этом случае в качестве базисных функций используются комплексные экспоненциальные функции (7.23). Поэтому коэффициенты Сп ряда (7.36) становятся комплексными. Они вычисляются по формуле

где, как и в формуле (7.6), индексная переменная п может быть как положительным, так и отрицательным целым числом.
При использовании комплексной формы ряда Фурье (7.36) спектром амплитуд периодического сигнала x(t) называют множество абсолютных величин комплексных коэффициентов Фурье Сп

а спектром фаз — множество главных аргументов этих коэффициентов

Множество величин {С%}^>=_<х> называется спектром мощности периодического сигнала, а множество комплексных чисел {Сп — спектральной последовательностью периодического сигнала. Именно эти три характеристики (спектр амплитуд, спектр фаз и спектр мощности) относятся к основным спектральным характеристикам периодического сигнала.
В отличие от амплитудного и фазового спектров периодического сигнала, представленного в форме тригонометрического ряда Фурье (7.24), спектры того же сигнала, построенные с использованием комплексных коэффициентов Фурье (7.37), оказываются двухсторонними. Это является следствием наличия в (7.36) «отрицательных частот» пО. (для отрицательных значений п). Последние, разумеется, не существуют в реальности. Они только отражают используемое при формировании комплексного ряда Фурье представление экспоненциальной гармонической функции ет в виде единичного вектора, вращающегося по часовой стрелке с угловой скоростью со.
Если существует изображение по Лапласу базового импульса периодического сигнала ХТ(р) = L{xT(t)}, то спектр амплитуд и спектр фаз периодического сигнала можно вычислять по формулам 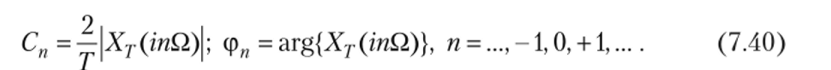
Известны и успешно применяются на практике алгоритмы так называемого быстрого преобразования Фурье, благодаря которым удается настолько снизить время вычисления коэффициентов Фурье, что спектры сигналов при их обработке получают практически в режиме реального времени [2].
В заключение отметим три наиболее важных свойства спектральных характеристик периодического сигнала.
1. Если x(t) — четная функция, то мнимые составляющие всех комплексных коэффициентов Фурье Im{Cw} равны нулю и, напротив, если эта функция нечетная, то вещественные составляющие всех комплексных коэффициентов Фурье Re{C„} равны нулю.
2. В точке разрыва первого рода t = tr функции x(t) сумма ряда Фурье S(t) равна полусумме предельных значений функции при приближении аргумента к точке разрыва t = tr слева и справа, т.е.
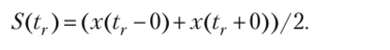
Примечание: если значения функции х{€) на концах +Г) базового импульса xT(t) не равны между собой, то при периодическом продолжении импульса эти точки становятся точками разрыва первого рода.
3. Мощности периодического сигнала во временной и частотной областях равны между собой, т.е.

Это соотношение выражает теорему Парсеваля.
Наличие в формуле (7.36) «отрицательных частот» nQ. (для гг < 0) иногда отмечают как недостаток комплексной формы ряда Фурье. Однако именно эта форма позволяет естественным образом распространить результаты спектрального анализа периодических детерминированных сигналов на сигналы, описываемые непериодическими функциями времени.
7. Что такое оценка сигнала? Укажите основные параметры оценки сигнала.
9. Что такое эффективная длительность сигнала? Как можно определить эффективную длительность сигнала?
Эффективная длительность сигнала определяется как интервал времени, внутри которого сосредоточена заданная часть (например 90 %) полной энергии сигнала.
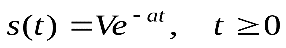
Знание длительности сигнала позволяет решать задачи эффективного использования времени, предоставляемого для передачи сообщений.
Для описания одного и того же сигнала в зависимости от решаемых задач могут быть использованы различные математические представления:
-временное представление,
-спектральное (частотное) представление.
Временное представление – это описание сигнала с помощью функций времени. Оно определяет свойство и параметры сигнала во временной области (форму, длительность сигнала, энергию, мощность).
Однако при практическом применении сигналов важно знать их свойства не только во временной, но и в частотной области. В этом случае при анализе и расчетах сигналы представляются своими частотными характеристиками, что облегчает решение многих практических задач обработки сигнала. Обычно частотные характеристики называют частотными спектрами, или спектрами, сигнала. Принято и другое название – спектральные характеристики. Определение спектра сигнала составляет задачу спектрального анализа. В основе спектрального анализа лежит разложение сигнала на спектральные составляющие. Математические методы спектрального анализа различаются для периодических и непериодических сигналов.
10. Что такое пороговая длительность сигнала? Как можно определить
пороговую длительность сигнала?
11. Что такое эффективная ширина спектра сигнала? Как можно определить эффективную ширину спектра сигнала?
Знание ширины спектра позволяет решать задачи эффективного использования диапазона радиочастот.
Второй наиболее важной характеристикой с точки зрения транспортировки сигнала по каналу связи является ширина спектра сигнала ΔFS, Гц, или эффективная ширина спектра сигнала ΔFSE, Гц. Эффективной шириной спектра сигнала (шириной спектра сигнала) называется диапазон частот, в пределах которой сконцентрировано 90...99% энергии сигнала. Этот параметр даёт представление о скорости изменения сигнала внутри интервала его существования. Эффективная ширина спектра сигнала рассчитывается по формуле

Обычно как сигнал, так и его спектр, не бывают строго ограничены по времени или по частоте. Поэтому необходимо определить понятия длительность сигнала и ширина его спектра. При этом обычно используют два подхода:
энергетический;
информационный.
При энергетическом подходе длительность сигнала или ширину его спектра определяют по заданной доле от полной энергии сигнала. Так, например, для сигнала в виде прямоугольного импульса длительностью t спектральная плотность имеет бесконечно широкий спектр, однако анализ показывает, что первый лепесток спектра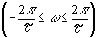 содержит 90% от полной энергии импульса, а сумма первого и второго содержит 90% от полной энергии импульса, а сумма первого и второго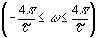 уже 95%. Аналогично можно рассуждать и о длительности бесконечно длящегося сигнала с конечной энергией. уже 95%. Аналогично можно рассуждать и о длительности бесконечно длящегося сигнала с конечной энергией.
При информационном подходе важное значение имеет форма сигнала: чем шире взята за основу условная ширина его спектра, тем ближе по форме к исходному может быть воспроизведенный по ограниченному спектру сигнал. Иногда ширину спектра определяют по уровню 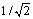 от максимального значения. Для колоколообразных импульсов принята величина е-1/2=0,606 от максимума. Ширина спектра и длительность сигнала взаимосвязаны. Для выявления этой связи определяют так называемые эффективные длительность и ширину спектра, которые вычисляют с помощью следующих соотношений: от максимального значения. Для колоколообразных импульсов принята величина е-1/2=0,606 от максимума. Ширина спектра и длительность сигнала взаимосвязаны. Для выявления этой связи определяют так называемые эффективные длительность и ширину спектра, которые вычисляют с помощью следующих соотношений:
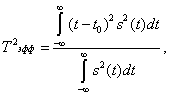
где 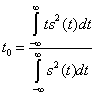 середина импульса; середина импульса;

Полная длительность сигнала равна 2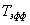 , а полная ширина спектра , включая и отрицательные частоты, 2 , а полная ширина спектра , включая и отрицательные частоты, 2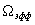 , Произведение длительности на полосу равно: , Произведение длительности на полосу равно:

Произведение 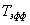 * *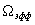 зависит от формы сигнала, но не может быть меньше 0.5(только для импульсов гауссовой формы это произведение равно 0.5). Не для всех сигналов данные интегралы имеют смысл(сходятся). Для определения зависит от формы сигнала, но не может быть меньше 0.5(только для импульсов гауссовой формы это произведение равно 0.5). Не для всех сигналов данные интегралы имеют смысл(сходятся). Для определения 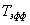 и и 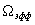 необходимо, чтобы функция s(t) убывала бы быстрее, чем 1/t, а функция S( w ) быстрее, чем 1/ w . необходимо, чтобы функция s(t) убывала бы быстрее, чем 1/t, а функция S( w ) быстрее, чем 1/ w .
Для сигналов, не удовлетворяющих этим условиям, и применяют энергетический, либо информационный критерий, но следует помнить, что с уменьшением длительности сигнала ширина его спектра увеличивается, т.е. произведение длительности на ширину спектра для данного типа сигнала величина постоянная.
12. Как с помощью маркеров на временной диаграмме можно определить
частоту (амплитуду) гармонического колебания
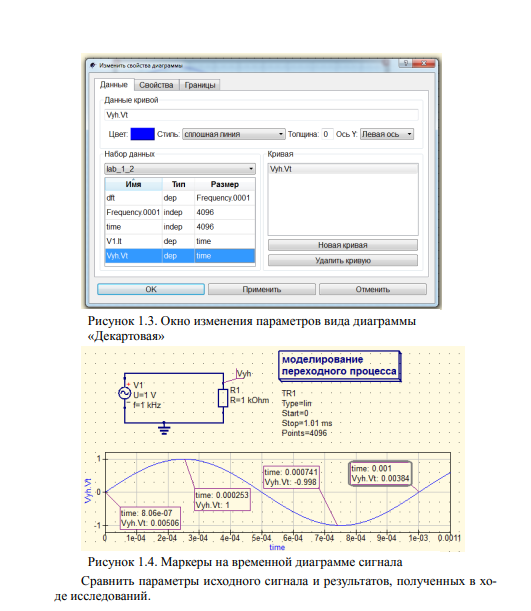
Измерение временных и амплитудных параметров Для измерения временных и амплитудных параметров сигнала в пакете QUCS используют маркеры. Вставить маркер в любую точку диаграммы можно через вкладку «Вставка»>> «Установить маркер на диаграмме», либо кнопкой «Маркер (М1)» на панели инструментов. Так, на рисунке 1.4 маркеры установлены в точках перехода диаграммы через нулевой уровень и точках графика, достигающих экстремума. По значениям этих точек можно определить, например, амплитуду и период повторения сигнала (либо его частоту).
13. Как на графике АЧХ спектра определить ширину спектра сигнала по
пороговому критерию?
Для определения ширины спектра в качестве порога используем уровень, равный 10% от величины наибольшей гармоники. Для повышения точности измерений целесообразно растянуть график АЧХ спектра по вертикали.
14. Что такое прямое преобразование Фурье? Приведите необходимые
пояснения.
15. Что такое обратное преобразование Фурье? Приведите необходимые
пояснения.
Преобразование Фурье - это математическая операция, которая преобразует функцию от времени в частотные компоненты. Обратное преобразование Фурье (inverse Fourier transform - IFT) преобразует частотные компоненты во временные компоненты.



16. Что понимается под ортогональной системой базисных функций?
Дайте пояснения по каждому признаку.
Одним из наиболее удобных способов описания исследуемого сигнала является его аналитическое представление с помощью системы некоторых взаимосвязанных функций времени, которую называют базисно.
ОРТОГОНАЛЬНЫЕ ФУНКЦИИ. Пусть в некотором линейном пространстве функции определено скалярное произведение. Две функции этого пространства  и и 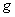 ортогональны, если их скалярное произведение равно нулю. Например, четная функция ортогональны, если их скалярное произведение равно нулю. Например, четная функция  и нечетная и нечетная 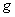 ортогональны на отрезке ортогональны на отрезке  относительно скалярного произведения относительно скалярного произведения
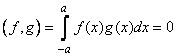 . .
Свойство ортогональности функций (в данном случае сигналов) обязательно связано с интервалом их определения (рис. 2.4). Например, гармонические сигналы 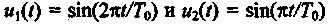 ортогональны на любом интервале времени, длительность которого равна целому числу полупериодов ортогональны на любом интервале времени, длительность которого равна целому числу полупериодов (рис. 2.4, а). Следовательно, в первом периоде сигналы (рис. 2.4, а). Следовательно, в первом периоде сигналы ортогональны на интервале ортогональны на интервале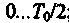 ; однако на интервале ; однако на интервале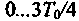 они уже неортогональны. На рис. 2.4,б сигналы ортогональны вследствие разновременности их появления. они уже неортогональны. На рис. 2.4,б сигналы ортогональны вследствие разновременности их появления.
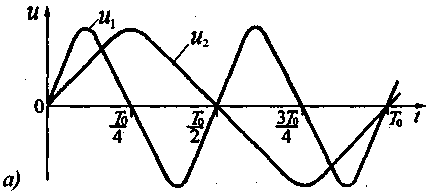

+Рис. 2.4. Ортогональные сигналы: а — ортогональность на интервале; б— ортогональность из-за разновременности появления
17. Какая ортогональная система базисных функций называется полной?
Укажите признаки полноты.
Если система ортогональных функций полная, то к ней нельзя добавить ни
одной новой функции, которая была бы ортогональна одновременно ко всем дру-
гим функциям данной системы.
18. Какая система базисных функций называется ортонормированной? Укажите условия нормировки.
Представление сигнала простыми моделями существенно упрощается, если выбрана система базисных функций простыми моделями существенно упрощается, если выбрана система базисных функций , обладающих свойством ортонормированности (ортогональности и нормированности). В математике такую систему базисных функций называют ортонормированным базисом. , обладающих свойством ортонормированности (ортогональности и нормированности). В математике такую систему базисных функций называют ортонормированным базисом.
ОРТОНОРМИРОВАННАЯ СИСТЕМА ФУНКЦИЙ
ОРТОНОРМИРОВАННАЯ СИСТЕМА ФУНКЦИЙ относительно некоторого скалярного
произведения — система функций  такая, что скалярный квадрат каждой функции семейства равен единице, а скалярные произведения любых двух различных функций системы равны нулю. Например, система функций: такая, что скалярный квадрат каждой функции семейства равен единице, а скалярные произведения любых двух различных функций системы равны нулю. Например, система функций:
 , где , где  , ,
образует О. с. ф. относительно скалярного произведения:
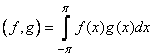 . .
Одной из главных задач теории О. с. ф. является задача о разложении функции в ряд по О. с. ф.:
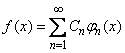 (*) (*)
Предполагая возможность почленного интегрирования, получаем формулу для коэффициентов 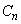 (скалярное произведение в данном случае записывается: (скалярное произведение в данном случае записывается:
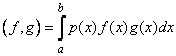 , ,
где 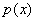 — некоторая функция — «вес»): — некоторая функция — «вес»):
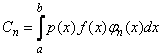 . .
Если 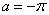 , , 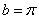 , , 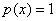 , то разложение (*) — обычное разложение функции , то разложение (*) — обычное разложение функции  в Фурье ряд. в Фурье ряд.
Теория О. с. ф. находит свое основное применение в решении краевых задач уравнений математической физики. |
 Скачать 0.69 Mb.
Скачать 0.69 Mb.

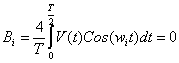
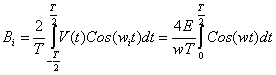
 (2.1.)
(2.1.)

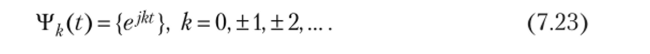
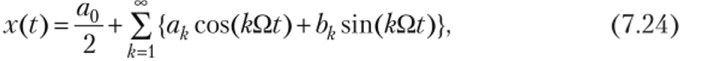

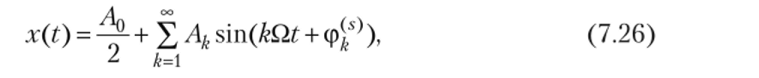
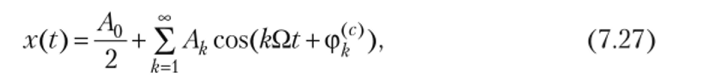

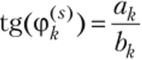


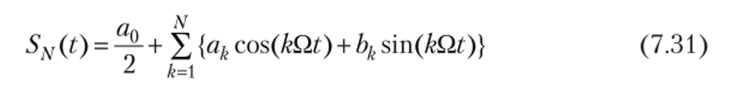




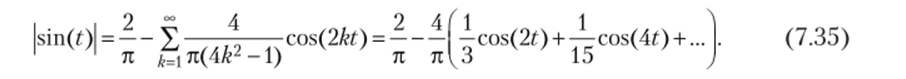
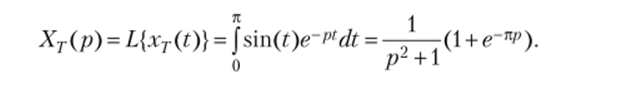
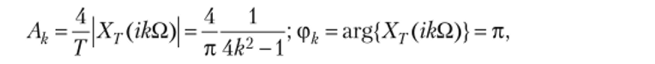 что совпадает с прежними результатами.
что совпадает с прежними результатами.


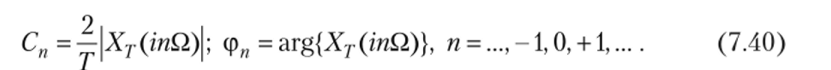
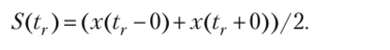

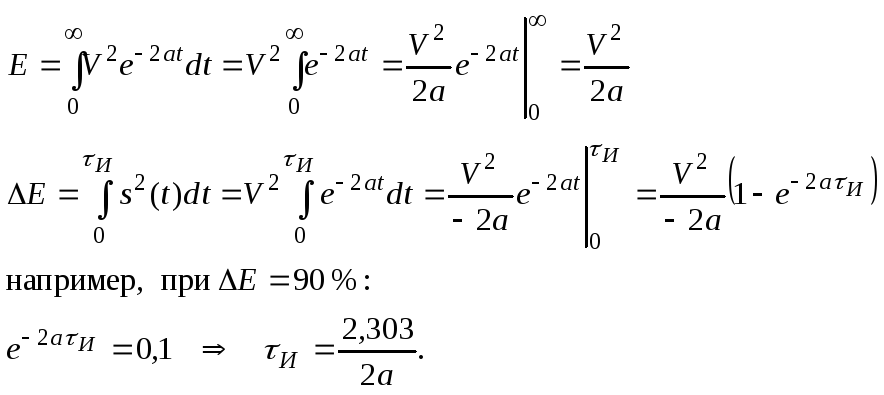

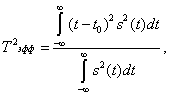
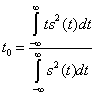 середина импульса;
середина импульса;





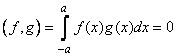 .
.

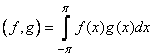 .
.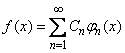 (*)
(*)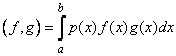 ,
,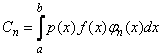 .
.