Изучение многоканальной замкнутой системы. Изучение многоканальной замкнутой системы ЛР. Краткие сведения об объекте моделирования
 Скачать 215.52 Kb. Скачать 215.52 Kb.
|
|
Цель работы Изучение многоканальной замкнутой системы массового обслуживания с неограниченным временем ожидания требований в системе. Входной поток требований – простейший. Он наиболее полно соответствует реалиям жизни и характеризуется следующими особенностями: поступление требований в систему на обслуживание происходит по одному, то есть вероятность прибытия двух и более требований одновременно очень мала и ею можно пренебречь (поток требований ординарный); вероятность поступления последующих требований не зависит от вероятностей поступления предыдущих – поток требований без последействия; поток требований стационарный. Краткие сведения об объекте моделирования Функционирование многоканальной замкнутой системы массового обслуживания можно описать через все возможные ее состояния и интенсивности перехода из одного в другое. Основными параметрами функционирования СМО являются вероятности состояния системы, то есть вероятности наличия 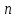 требований (покупателей, рабочих, заданий, машин, неполадок) в системе – требований (покупателей, рабочих, заданий, машин, неполадок) в системе – 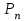 . Так, вероятность . Так, вероятность 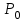 характеризует состояние, когда в системе нет требований и все каналы обслуживания простаивают, характеризует состояние, когда в системе нет требований и все каналы обслуживания простаивают, 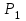 – в системе находится только одно требование и т. д. – в системе находится только одно требование и т. д.Важным параметром функционирования системы массового обслуживания является также среднее число требований, находящихся в системе 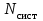 (то есть в очереди и на обслуживании), и средняя длина очереди (то есть в очереди и на обслуживании), и средняя длина очереди 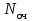 . . Исходными параметрами, характеризующими СМО, являются: число каналов обслуживания N (касс, компьютеров, кранов, ремонтных бригад), число требований m (покупателей, рабочих, заданий, машин, неполадок), интенсивность поступления одного требования на обслуживание 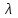 , интенсивность обслуживания требований , интенсивность обслуживания требований 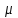 . .Интенсивность поступления на обслуживание одного требования определяется как величина, обратная времени возвращения требования, – 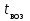 : :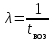 . .Интенсивность обслуживания требований определяется как величина, обратная времени обслуживания одного требования, – 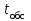 . .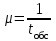 . .Представим все возможные состояния системы массового обслуживания в виде размеченного графа состояний (рис. 2.1). Каждый прямоугольник графа определяет одно из возможных состояний, количественно оцениваемое вероятностью 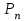 (наличие в системе (наличие в системе 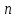 требований). Стрелочки указывают, в какое состояние система может перейти и с какой интенсивностью. При этом в многоканальной СМО необходимо различать два случая: требований). Стрелочки указывают, в какое состояние система может перейти и с какой интенсивностью. При этом в многоканальной СМО необходимо различать два случая:- число требований 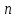 , поступивших в систему, меньше числа каналов обслуживания N, то есть все они находятся на обслуживании 0 n < N; , поступивших в систему, меньше числа каналов обслуживания N, то есть все они находятся на обслуживании 0 n < N;- число требований 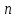 , поступивших в систему, больше или равно числу каналов обслуживания N, то есть N требований обслуживаются, а остальные , поступивших в систему, больше или равно числу каналов обслуживания N, то есть N требований обслуживаются, а остальные 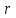 ожидают в очереди ( ожидают в очереди (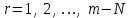 ). ).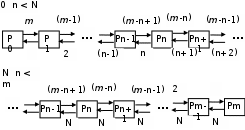 Рис. 1. Размеченный граф состояний многоканальной замкнутой СМО Первый прямоугольник с вероятностью 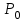 определяет состояние системы массового обслуживания, при котором все каналы простаивают из-за отсутствия требований в ней. Из этого положения СМО может перейти только в состояние определяет состояние системы массового обслуживания, при котором все каналы простаивают из-за отсутствия требований в ней. Из этого положения СМО может перейти только в состояние 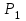 , и тогда в ней появится одно требование, потому что входной поток требований – ординарный. С интенсивностью m система может перейти также из состояния , и тогда в ней появится одно требование, потому что входной поток требований – ординарный. С интенсивностью m система может перейти также из состояния 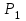 , в состояние , в состояние 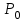 ; когда в системе находилось одно требование, оно было обслужено раньше, чем появилось новое. Из состояния ; когда в системе находилось одно требование, оно было обслужено раньше, чем появилось новое. Из состояния 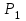 система массового обслуживания может перейти с интенсивностью система массового обслуживания может перейти с интенсивностью 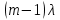 в состояние в состояние 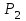 ; тогда в системе появятся два требования. С интенсивностью ; тогда в системе появятся два требования. С интенсивностью 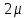 система может перейти также из состояния система может перейти также из состояния 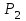 в состояние в состояние 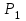 ; когда в системе находилось два требования, но одно из них было обслужено раньше, чем появилось новое, и т. д. ; когда в системе находилось два требования, но одно из них было обслужено раньше, чем появилось новое, и т. д.Вначале рассмотрим установившийся режим работы системы массового обслуживания, когда основные вероятностные характеристики ее постоянны во времени, например в течение часа. В этом случае интенсивности входных и выходных потоков для каждого состояния будут сбалансированы. Для случая, когда число требований 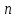 , поступивших в систему, меньше числа каналов обслуживания N, – 0 n < N: , поступивших в систему, меньше числа каналов обслуживания N, – 0 n < N: 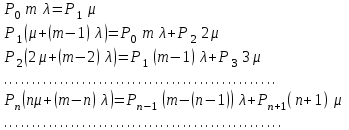 Для случая, когда число требований 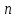 , поступивших в систему, больше или равно числу каналов обслуживания N, – N n m: , поступивших в систему, больше или равно числу каналов обслуживания N, – N n m: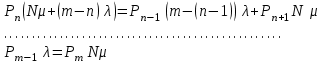 Обозначим величину 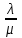 как и раньше, через как и раньше, через 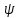 и назовем ее коэффициентом загрузки. и назовем ее коэффициентом загрузки.Рассмотрим вначале первый случай, когда число требований, находящихся в системе, меньше числа каналов обслуживания – 0 n < N. Из первого уравнения можно найти значение 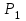 : :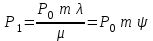 . .Из второго уравнения найдем значение 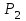 : :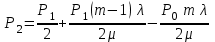 Но 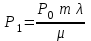 – из первого уравнения, следовательно, первый и третий члены сокращаются: – из первого уравнения, следовательно, первый и третий члены сокращаются: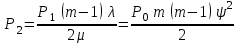 . .Из третьего уравнения найдем значение 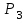 : :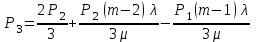 Но 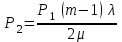 , следовательно, первый и третий члены сокращаются: , следовательно, первый и третий члены сокращаются: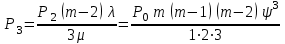 и т. д. и т. д.Аналогичные выражения можно получить и для других состояний. Анализируя полученные результаты, вычисляем рекуррентное выражение для определения вероятности состояния системы, когда число требований, находящихся в системе 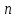 , меньше числа каналов обслуживания N: , меньше числа каналов обслуживания N: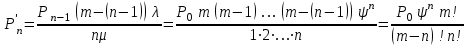 . .Рассмотрим теперь второй случай, когда число требований, находящихся в системе, больше или равно числу каналов обслуживания – N n m. В этой ситуации рекуррентное выражение для определения вероятности состояния системы будет записано в таком виде: 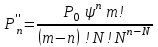 . .Используя очевидное равенство 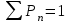 от n = 0 до m, получим: от n = 0 до m, получим: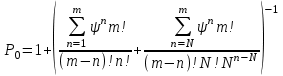 Теперь рассмотрим неустановившийся режим работы СМО, когда ее основные вероятностные характеристики зависят от времени. В этом случае интенсивности входных и выходных потоков для каждого состояния будут сбалансированы, но уже с учетом производных вероятностей. Таким образом, мы будем иметь систему обыкновенных дифференциальных уравнений, описывающих функционирование одноканальной замкнутой системы при неустановившемся режиме. Для составления системы обыкновенных дифференциальных уравнений, описывающей функционирование СМО с пуассоновским потоком, существует мнемоническое правило: производная 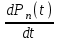 вероятности пребывания системы в состоянии n равна алгебраической сумме нескольких членов; вероятности пребывания системы в состоянии n равна алгебраической сумме нескольких членов;число членов этой суммы равно количеству стрелок на графе состояний системы, соединяющих состояние n с другими; если стрелка направлена в рассматриваемое состояние n, то член берется со знаком «плюс»; если стрелка направлена из рассматриваемого состояния n, то член берется со знаком «минус»; каждый член суммы равен произведению вероятности того состояния, из которого направлена стрелка, на интенсивность потока событий, переводящего систему по данной стрелке. В соответствии с размеченным графом состояний (рис. 1) эта система обыкновенных дифференциальных уравнений будет выглядеть так: • для случая, когда число требований n, поступивших в систему, меньше числа каналов обслуживания N, – 0 n < N: 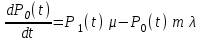 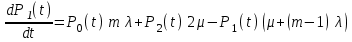 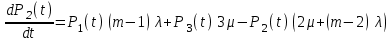 …………………………………………………………. 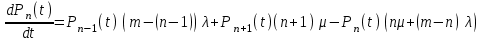 • для случая, когда число требований n, поступивших в систему, больше или равно числу каналов обслуживания N, – N n m: 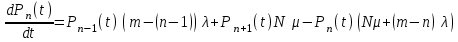 ………………………………………………………… 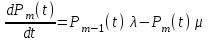 Как можно заметить, требуется большая вычислительная работа для определения основных параметров функционирования комплекта машин. Можно пойти, как и в предыдущей задаче, несколькими путями: предварительный расчет 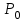 для различного числа каналов обслуживания и для разнообразных значений коэффициента использования у (табл. 1); для различного числа каналов обслуживания и для разнообразных значений коэффициента использования у (табл. 1);использование системы Mathcad. Обоими путями воспользуемся далее в ходе работы. Табл. 1 – Значения коэффициента использования y
Выполнение работы  Вначале рассмотрим установившийся режим работы системы массового обслуживания, когда основные вероятностные характеристики ее постоянны во времени. Вначале рассмотрим установившийся режим работы системы массового обслуживания, когда основные вероятностные характеристики ее постоянны во времени.Рис. 2. Определение параметров функционирования многоканальной замкнутой СМО в системе Mathcad. Теперь рассмотрим неустановившийся режим работы СМО, когда ее основные вероятностные характеристики зависят от времени. В этом случае интенсивности входных и выходных потоков для каждого состояния будут сбалансированы, но уже с учетом производных вероятностей. Таким образом, мы будем иметь систему обыкновенных дифференциальных уравнений, описывающих функционирование одноканальной замкнутой системы при неустановившемся режиме. На рис. 3 представлены начальные исходные данные и система дифференциальных уравнений, описывающая функционирование многоканальной замкнутой СМО при неустановившемся режиме работы. На рис. 4 дано представление системы дифференциальных уравнений в виде, доступном для решения ее в Mathcad. По существу, здесь показаны правые части системы уравнений в виде вектора-столбца. Каждый его элемент определяет значение правой части соответствующего дифференциального уравнения на любом шаге интегрирования (решения).  Там же даны начальные значения искомых параметров в виде вектора-столбца. В нижней части рисунка определены начальное и конечное время интегрирования и число шагов решения системы дифференциальных уравнений. Там же даны начальные значения искомых параметров в виде вектора-столбца. В нижней части рисунка определены начальное и конечное время интегрирования и число шагов решения системы дифференциальных уравнений. Рис. 3 - Описание функционирования многоканальной замкнутой СМО при неустановившемся режиме Рис. 3 - Описание функционирования многоканальной замкнутой СМО при неустановившемся режимеРис. 4 - Представление совокупности дифференциальных уравнений в виде, доступном для решения ее в системе Mathcad На рис. 5 приводится решение системы дифференциальных уравнений многоканальной замкнутой СМО с использованием встроенной функции rkfixed(P,to,t1,n,D), реализующей метод Рунге-Кутта с фиксированным шагом. 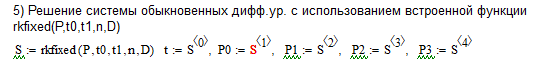 Рис. 5. Решение системы дифференциальных уравнений многоканальной Рис. 5. Решение системы дифференциальных уравнений многоканальной замкнутой СМО 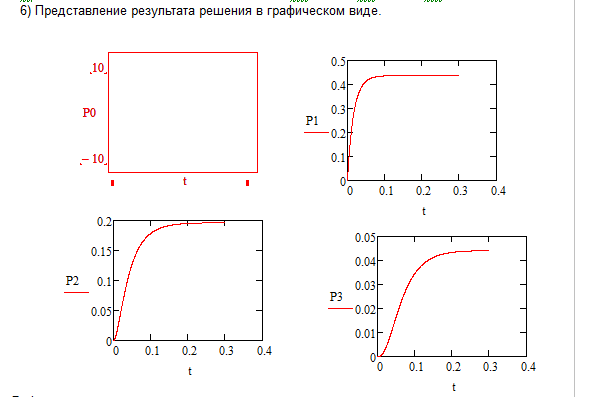 На рис. 6 приведено графическое решение системы дифференциальных уравнений для остальных четырех искомых параметров. На рис. 6 приведено графическое решение системы дифференциальных уравнений для остальных четырех искомых параметров.Рис. 6. Результаты решения системы дифференциальных уравнений многоканальной замкнутой СМО Выводы: Другими словами, на рис. 6 представлено поведение искомых параметров 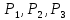 – вероятности наличия в системе одного, двух, и трех требований соответственно в зависимости от времени протекания процесса. – вероятности наличия в системе одного, двух, и трех требований соответственно в зависимости от времени протекания процесса.Анализируя графическое решение системы обыкновенных дифференциальных уравнений, описывающей функционирование заданной многоканальной замкнутой СМО, можно заметить, что примерно через 0,2 часа она переходит в установившийся режим работы. При этом значения вероятностей состояний режима paботы системы при решении совокупности обыкновенных дифференциальных уравнений практически полностью соответствуют решению системы алгебраических уравнений для установившегося режима работы: 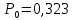 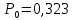 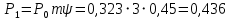 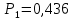 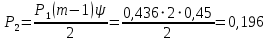 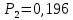 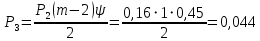 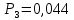 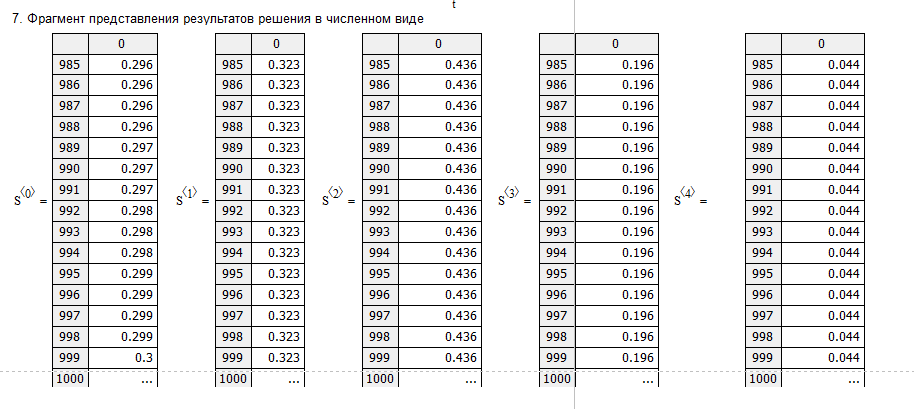 На рис. 7 представлен фрагмент результатов решения системы обыкновенных дифференциальных уравнений в численном виде. На рис. 7 представлен фрагмент результатов решения системы обыкновенных дифференциальных уравнений в численном виде.Рис. 7. Фрагмент результатов решения системы обыкновенных дифференциальных уравнений в численном виде для многоканальной замкнутой СМО |