Курсовая работа по дисциплине Геодезия Теодолитная съёмка
 Скачать 7.48 Mb. Скачать 7.48 Mb.
|
|
КУРСОВАЯ РАБОТА по дисциплине Геодезия «Теодолитная съёмка» Содержание Введение . Сущность теодолитной съёмки . Полевые работы при теодолитной съёмке .1 Проложение теодолитных ходов и привязка их к пунктам опорной геодезической сети .2 Съёмка ситуации местности . Камеральные работы при теодолитной съёмке .1Обработка результатов полевых измерений .2 Прямая и обратная геодезические задачи .3 Вычисление координат вершин теодолитного хода .4 Построение плана теодолитной съёмки Заключение Список использованной литературы Введение Геодезия - наука об определении формы и размеров Земли, об измерениях на земной поверхности, вычислительной обработке их для построения карт, планов, профилей и для решения инженерных, экономических и других задач. Геодезия (в переводе с греч. «землеразделение») возникла в глубокой древности и развивалась с ростом потребностей человека в жилье, делении земельных массивов, изучении природных богатств и их освоении. Научными задачами геодезии являются: − установление систем координат; − определение формы и размеров Земли и ее внешнего гравитационного поля и их изменений во времени; − проведение геодинамических исследований (определение горизонтальных и вертикальных деформаций земной коры, движений земных полюсов, перемещений береговых линий морей и океанов и др.). Научно-технические задачи геодезии в обобщенном виде заключаются в следующем: − определение положения точек в выбранной системе координат; − составление карт и планов местности разного назначения; − обеспечение топографо-геодезическими данными нужд обороны страны; − выполнение геодезических измерений для целей проектирования и строительства, землепользования, кадастра, исследования природных ресурсов и др. . Сущность теодолитной съемки Теодолитной съёмкой называется горизонтальная или контурная съёмка местности, которая выполняется с помощью теодолита. Теодолитом измеряются горизонтальные углы и углы наклона. Линии измеряются стальной лентой и дальномерами различных конструкций. По результатам теодолитной съёмки может быть составлении план без изображении рельефа. Для получения плана с изображением рельефа необходимо произвести нивелирование поверхности, на которой выполнялась теодолитная съёмка. Сочетание теодолитной съёмки и нивелирования поверхности целесообразно применять для получения плана строительного участка. Процесс теодолитной съёмки складывается из следующих видов работ: проложение теодолитных ходов, привязка их к пунктам геодезической сети, съёмка ситуации. . Полевые работы при теодолитной съёмке .1 Проложение теодолитных ходов и привязка их к пунктам опорной геодезической сети Плановым обоснованием теодолитной съемки служат теодолитные ходы, которые прокладываются в виде замкнутых полигонов и разомкнутых ходов. При съемке населенного пункта или участка для строительства обычно на границе прокладывается замкнутый полигон. Для обеспечения съемки ситуации и для контроля измерений внутри полигона может быть проложен диагональный ход, например, 5 -7 - 8 - 2 (рис. 1, а). Разомкнутый теодолитный ход должен быть вытянутым, т. е. с углами поворота, по возможности, близкими к 180°, и прокладываться, как правило, между пунктами триангуляции или полигонометрии (рис. 1, б). Проложение теодолитных ходов начинается с закрепления на местности колышками или деревянными столбами вершин углов поворота. Точки углов поворота теодолитных ходов выбирают так, чтобы стороны между соседними точками было удобно измерять, а длины их были бы не более 350 м и не менее 20 м. Линии измеряют дважды, в прямом и обратном направлениях, с относительными ошибками не более 1:3000, 1:2000 и 1: 1500 в зависимости от условий местности, на которой измеряются линии. Длина теодолитного хода допускается при съемке масштаба 1:5000 - 4 км; 1: 2000 - 2 км; 1:1000 - 1 км. Углы поворота в теодолитных ходах измеряют обычно вправо по ходу лежащие. Измерения выполняются при двух положениях вертикального круга и за окончательный результат принимается среднее из двух измерений, если разница из этих измерений не превышает двойной точности прибора. Углы наклона линий измеряют с помощью вертикального круга теодолита. Результаты угловых и линейных измерений записывают в журнал установленной формы. Пример записи измерения углов и линий в замкнутом полигоне с диагональным ходом показан в табл. 1. Средние значения горизонтальных проложений линий показаны на рис. 2. Для получения исходных координат и дирекционного угла теодолитного хода его нужно привязать к пунктам триангуляции или полигонометрии, координаты которых известны. Если ход проходит через пункт А опорной сети (рис. 3,а), то привязка заключается в измерении примычных углов в этой точке для передачи дирекционного угла на линию теодолитного хода, например, 3 - 4. Если теодолитный ход не проходит через пункт опорной сети, то в этом случае от одного из пунктов хода прокладывают наиболее короткий теодолитный ход до пункта опорной сети, и измеряют в этом ходе углы и линии для передачи координат и дирекционного угла, например, на пункт 8 и дирекционного угла на линию 8 - 9 (рис. 3, б).  Рис.1. Схемы теодолитных ходов: а- замкнутого; б- разомкнутого. 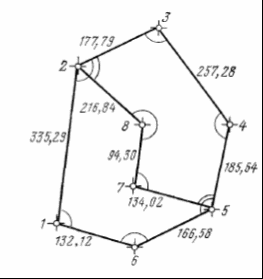 Рис.2. Схема измерения углов и линий основного (замкнутого) и диагонального теодолитных ходов. 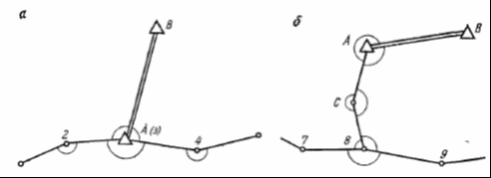 Рис.3. Схемы привязки теодолитных ходов к пунктам геодезической сети. теодолитный съемка геодезический камеральный Таблица.1 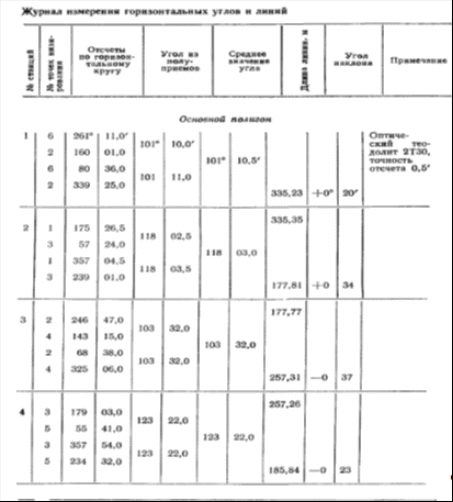   2.2 Съёмка ситуации местности Для съемки ситуации применяются различные способы, изложенные ниже. .Способ перпендикуляров. Этот способ применяется при съемке ситуации и местных предметов, имеющих правильные геометрические формы, например, зданий, а также криволинейных контуров, например, рек, дорог и других, вытянутых в длину контуров. 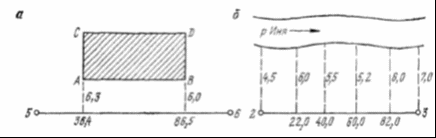 Рис.4. Схемы съёмки ситуации способом перпендикуляров.  Рис.5. Двухзеркальный экер: а - внешний вид экера; б - ход лучей в экере.  Рис.6. Способы съёмки ситуации: а - угловых засечек; б - линейных засечек. Перпендикуляры опускают из снимаемых точек здания или точек контура местности на стороны теодолитного хода. Например, положение точек А и В (рис. 4, а) определится длиной перпендикуляров и расстоянием от точки 5 теодолитного хода до этих перпендикуляров. Положение точек С и D получают по данным обмера здания рулеткой. На рис. 4,6 показана запись измерений при съемке берега реки способом перпендикуляров. Длина перпендикуляров допускается при съемке в масштабе 1:5000 - 10 м; 1:2000 - 8 м; 1:1000 - 6 м; 1:500 - 4 м. При такой длине перпендикуляры от снимаемых характерных точек опускаются на линию на глаз, более длинные - с помощью эккера. Двухзеркальный эккер (рис. 5, а) - простейший прибор, у которого два зеркала установлены под углом 45°. Зеркала прикреплены с внутренней стороны к корпусу, имеющему ручку с крючком, на котором подвешивается отвес. Над зеркалами в корпусе вырезаны окошечки. Луч из точки В (рис. 5, б), падающий на зеркало М под углом а, отражается и падает на другое зеркало N под углом β и, отразившись от этого зеркала, попадает в глаз наблюдателя по направлению СС′. Это направление пересекает линию АВ под углом 90°. Чтобы восставить перпендикуляр в точке С к линии АВ, держат эккер по отвесу в данной точке С так, чтобы зеркало М было обращено к вехе В. Затем, смотря в другое зеркало N и в окошечко над ним, выставляют веху В' по направлению изображения вехи В в этом зеркале. При опускании перпендикуляра из точки В' на АВ перемещаются с эккером по линии АВ до тех пор, пока изображение вехи В закроет веху В'. Эккер исправен, если угол между зеркалами установлен правильно, т. е. 45°. Поверка этого условия выполняется так: к прямой АВ в точке С восставляют эккером перпендикуляр по обеим вехам А и В. Если оба перпендикуляра сольются в одно направление, то эккер исправен. В противном случае, действуя исправительными винтами, изменяют положение зеркал, добиваются их совпадения. При применении эккера длины перпендикуляров допускаются до 80 м при съемке в масштабе 1:5000, до 60 м при съемке в масштабе 1:2000, до 40 м при съемке в масштабе 1:1000 и до 20 м при съемке в масштабе 1:500. . Способ угловых засечек. Этот способ выгодно применять при съемке труднодоступных контуров, например, при съемке противоположного берега реки. В этом случае при точках 2 и 3 (рис. 6, а) теодолитом измеряют одним полуприёмом углы β1, β2, β3 и β4. Засечки точек а и б должны быть под углом не менее 30° и не более 150°.  Рис.7. Способы съёмки ситуации: а - полярный; б - створов. Построением на плане этих углов получим точки а и б на противоположном, относительно линии теодолитного хода, берегу реки. . Способ линейных засечек. Способ применяется при съемке зданий (рис. 6,б). В этом случае положение точки А определяется измерением расстояний 6А, 6М и МА. Эти расстояния измеряются лентой или рулеткой, и они должны быть примерно равными. Для получения на плане точки А надо построить треугольник 6МА. Положение точки В определяется аналогично, но измеряются расстояния 6N, 6Q, NB и QB, причем NQ - часть стороны теодолитного хода 6 - 7. . Способ полярных координат или полярный способ. Суть полярного способа съемки ситуации заключается в том, что точки 1, 2, 3,... (рис. 7, а) определяются в системе полярных координат, т. е. горизонтальными углами β1, β2, β3 образованными начальным направлением 7 - 8 и расстояниями 7 - 1, 7 - 2, 7 - 3 от точки полюса 7 до снимаемых точек. Эти расстояния определяются с помощью нитяного дальномера и не должны превышать при съемке масштаба 1:5000 - 150 м; 1:2000 - 100 м; 1:1000 - 60 м. Углы измеряются одним полуприемом. Чтобы не делать вычислений, поступают так: совмещают нулевой штрих алидады с нулевым штрихом лимба и, вращая лимб, визируют на точку 8. Для съемки точек 1, 2, 3 вращением алидады последовательно визируют на дальномерную рейку, устанавливаемую на эти точки, и записывают отсчеты по лимбу, равные углам β1, β2, β3 и расстояния, взятые по дальномеру. Для контроля визируют вновь на точку 8 и делают отсчет, который не должен отличаться от нуля более 2'. Результаты измерений этим способом записывают в журнал. . Способ створов. Этот способ применяется при съемке точек, расположенных в створе линии теодолитного хода, либо в створе линии, опирающейся на точки теодолитного хода (рис. 7,б). При съемке ситуации составляется абрис. Абрис является схематическим чертежом, на котором показывают все снимаемые точки с соблюдением порядка и взаимного расположения контуров местности между собой и относительно опорных линий. Абрис составляется отдельно для каждой стороны теодолитного хода и снятой ситуации с этой стороны. Абрис ведут карандашом четко и аккуратно с записями всех выполненных при съемке угловых и линейных измерений. . Камеральные работы при теодолитной съёмке .1 Обработка результатов полевых измерений При теодолитной съемке получают геодезический журнал измерений углов, линий и абрис. Эти документы служат основным материалом для построения плана. Поэтому обработку результатов полевых измерений начинают с проверки правильности всех записей и вычислений, сделанных в журнале, а также вычислений поправок за наклон сторон теодолитного хода. Дальнейшая обработка измерений при теодолитной съемке складывается из следующих действий: обработка угловых измерений и вычисление дирекционных углов и румбов сторон, вычисление приращений и координат вершин теодолитного хода, построение плана участка теодолитной съемки. Угловая невязка замкнутого хода. Известно, что теоретическая сумма углов плоского многоугольника равна: где n- число углов многоугольника. Пусть практическая сумма измеренных углов замкнутого многоугольника (рис.4,а) равна ∑βn. Разность между практической суммой измеренных углов и теоретической суммой называется угловой невязкой полигона и обозначается через ƒβ. Для углов, измеренных теодолитом тридцатисекундной точности полным приемом, допустимая предельная невязка суммы углов определяется по формуле, Допустимая невязка распределяется с обратным знаком поровну на все углы с округлением до 0,1'.  Рис.8. Схемы обработки теодолитных ходов: а замкнутого; б - диагононального. Сумма всех поправок в углы должна равняться невязке ƒβ с обратным знаком, а сумма исправленных углов - удовлетворять формуле. Вычисление дирекционных углов и румбов сторон замкнутого хода. Исходный дирекционный угол а1 , например, стороны 1 - 2 хода (рис. 8,а) получают в результате привязки этой стороны к пунктам геодезической опорной сети и определяют для неё истинный или магнитный азимут. По известному дирекционному углу а1 и по исправленным углам β вычисляют дирекционные углы всех сторон замкнутого хода по формулам:  Последняя строка равенств контрольная. По дирекционным углам вычисляют румбы, пользуясь их зависимостью между собой. Угловая невязка разомкнутого теодолитного хода. На рис. 1, б показан разомкнутый ход, проложенный между пунктами В а С опорной сети. Координаты исходных точек А, В и С, D опорной сети и дирекционные углы а0 и ап известны. Для определения дирекционных углов разомкнутого теодолитного хода напишем формулы:  Сложив равенства, получим: Откуда Угловая невязка Допустимость угловой невязки ƒβ в разомкнутом ходе определяются по формуле .2 Прямая и обратная геодезические задачи При вычислительной обработке результатов измерений на местности, при проектировании инженерных сооружений и перенесении их в натуру возникает необходимость решать прямую и обратную геодезические задачи. Прямая геодезическая задача. Даны координаты х1 и у1 точки А начала линии АВ, ее горизонтальное проложение d и дирекционный угол а. Требуется определить координаты х2 и у2 точки В конца этой линии (рис. 9). Из рис. 9 видно, что координаты:  Разности координат конечной и начальной точек линии АВ, т.е. ∆х и ∆у называются приращением координат:   Рис.9. Прямая и обратная геодезические задачи. При помощи румбов приращения координат вычисляют по формулам:  Приращения координат имеют знаки, которые зависят от знака косинуса и синуса дирекционного угла или от названия румба линии:  Вычисление приращений координат выполняют с помощью таблиц натуральных значений sin и cos или с помощью вычислительных машин. Обратная геодезическая задача. Даны координаты х1 и у1 точки А начала линии АВ и координаты х2 и у2 точки В конца этой линии. Требуется определить длину и дирекционный угол или румб этой линии. Из рис.9 следует, что  r- определяет по таблицам натуральных значений тригонометрических функций или с помощью микрокалькулятора «Электроника». Название румба определяют по знакам ∆х и ∆у. Зная румб, можно вычислить дирекционный угол α. Расстояние d можно вычислить по формулам: 3.3 Вычисление координат вершин теодолитного хода Невязки в приращениях координат замкнутого полигона (рис. 8,а). Известно, что сумма проекций замкнутого полигона на любую координатную ось равна нулю, следовательно, теоретически алгебраическая сумма приращений координат должна быть Но так как результаты измерений углов и линий содержат ошибки, вследствие которых практически Величины ƒx и ƒy называются невязками в приращениях координат соответственно по оси абсцисс и по сои ординат. Прежде чем распределять эти невязки, надо убедиться в их допустимости, для чего необходимо вычислить невязку в периметре И определить её допустимость по формуле где P- периметр полигона. Если невязка в периметре допустима, то невязки ƒx и ƒy распределяют с обратным знаком соответственно на все приращения Δx и Δy пропорционально длинам линий с округлением до 0,01 м. Контролем вычисления поправок служит равенство: сумма поправок в приращениях по оси абсцисс и оси ординат должна равняться невязке с обратным знаком. Полученные поправки алгебраически прибавляют к соответствующим приращениям и получают исправленные приращения. Сумма исправленных приращений по каждой оси в замкнутом полигоне должна равняться нулю. После исправления приращений вычисляют координаты всех вершин полигона, пользуясь правилом: координата последующей точки равна координате предыдущей точки плюс соответствующее приращение. Для вычисления этих координат надо иметь исходные координаты, которые получают путем привязки теодолитного хода к опорной геодезической сети либо выбирают произвольно. Контролем вычисления координат является последовательное вычисление координат точек замкнутого полигона, чтобы в результате получить координаты исходной точки. Таблица. 2. Ведомость вычисления координат основного полигона.  Невязки в приращениях разомкнутого хода (см. рис. 1,6) определяются по формулам Координаты начального и конечного пунктов хода известны. Невязка ƒP в периметре вычисляется по формуле а её допустимость по формуле если ход проложен между пунктами теодолитного хода (см. рис. 8,б), то допустимость невязки определяется по формуле Распределение невязок ƒx и ƒy , вычисление исправленных приращений и координат пунктов разомкнутого хода выполняются так же, как и в замкнутом полигоне.  Контролем служит сумма исправленных приращений по оси абсцисс и оси ординат, равная разности соответствующих координат конечной и начальной точек хода. Последовательно вычисляя координаты хода по исходным координатам начального пункта, получаем координаты конечного пункта. Обработку угловых измерений, вычисление дирекционных углов и румбов, вычисление приращений и координат вершин теодолитного хода выполняют в специальной ведомости, которую принято называть ведомостью координат. Пример вычисления координат замкнутого теодолитного хода приведен в табл. 2. В графу 2 ведомости вычисления координат выписываются из журнала полевых измерений (табл. 1) средние значения горизонтальных углов хода, а в графу 6 средние значения длин линий, измеренных в прямом и обратном направлениях. При углах наклона, превышающих 1°, в длины линий вводится поправка за наклон. По формуле находится угловая невязка, которая в приведённом примере ƒβ =-1,2׳, т.е. меньше предельной невязки ƒβ доп =-2,4׳, вычисленной по формуле Следовательно, угловая невязка допустима, она распределяется с обратным знаком поровну на все измеренные углы. Исправленные углы записываются в графу 3. Сумма исправленных углов в замкнутом полигоне равна теоретической сумме, в приведенном примере равна 720°. По исходному дирекционному углу линии 1-2, равному 10°40' (графа 4), вычисляются дирекционные углы всех остальных сторон по формулам:  , т.е. , т.е. . .Последняя строка контрольная. Таблица 3. Ведомость вычислений координат диагонального хода с точки 5 на точку 2 основного полигона.  .4 Построение плана теодолитной съёмки Построение плана теодолитной съемки начинают с построения на чертежной бумаге координатной сетки со сторонами квадратов 10 см. Такую сетку удобно строить при помощи металлической линейки Ф. В. Дробышева ЛД-1 длиной 70,711 см, равной диагонали квадрата со стороной 50 см. 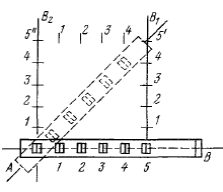 Рис.10. Схема построения координатной сетки при помощи линейки ЛД-1. На этой линейке вдоль ее оси вырезаны шесть окошек, скошенные края которых имеют вид дуг радиусами 10, 20, 30, 40 и 50 см. Для построения координатной сетки линейку ЛД-1 кладут на лист бумаги вблизи ее края (рис. 10) так, чтобы вся координатная сетка разместилась на листе и вдоль продольного скошенного ребра линейки остро отточенным карандашом проводят линию АВ. Затем линейку накладывают на эту линию и карандашом по скошенным краям окошек проводят короткие дуги 1, 2, . . . , 5, пересекающие линию АВ. Перекладывают линейку перпендикулярно к линии АВ, совмещают нуль-пункт линейки с точкой 5 линии АВ и проводят короткие дуги 1', 2', ...,5'. После этого кладут линейку по направлению АВ1 так, как это показано на рис. 10, и по ее скошенному концу проводят дугу. В пересечении этой дуги с дугой 5' получают точку, лежащую на перпендикуляре 5В1 к линии АВ. Аналогично получают перпендикуляр АВ2 и дуги на нем 1", 2", ..., 5". Затем, соединяя прямыми одноименные дуги, получают сетку квадратов. Сетку с малым числом квадратов можно построить при помощи выверенной чертежной линейки, масштабной линейки и циркуля-измерителя. Для этой цели на листе бумаги проводят, приблизительно по диагоналям листа бумаги, две пересекающиеся прямые линии. От точки их пересечения откладывают равные отрезки. Концы отрезков соединяют прямыми линиями и получают прямоугольник. На сторонах этого прямоугольника, пользуясь масштабной линейкой и циркулем-измерителем, откладывают отрезки по 10 см. Соответствующие точки на противоположных сторонах прямоугольника соединяют прямыми, которые образуют координатную сетку. Правильность построения сетки необходимо тщательно проверить. Проверка проводится сравнением длин сторон и диагоналей каждого квадрата при помощи циркуля-измерителя и масштабной линейки отклонение не должно превышать 0,1 мм. После построения и проверки сетки ее подписывают таким образом, чтобы весь участок разместился приблизительно посредине листа. Далее, при помощи масштабной линейки и циркуля-измерителя, строят вершины теодолитных ходов по их координатам. Правильность наложенных на план вершин теодолитного хода проверяется путем сравнения длин сторон хода, измеренных на плане, с их размерами, записанными в координатной ведомости. Составление контурного плана местности выполняется на основе нанесенных на план теодолитных ходов по данным абриса. Способ нанесения контуров на план определяется способом их съемки на местности. Если съемка ситуации проводилась способом перпендикуляров, то на план ее наносят с помощью линейки, треугольника, масштабной линейки и циркуля- измерителя в том же порядке, в каком составлялся абрис. Для нанесения точек, снятых способом угловых засечек, используется транспортир. Точки, снятые способом линейных засечек, на план наносят при помощи циркуля-измерителя и масштабной линейки. Точки, снятые полярным способом, наносят на план при помощи транспортира, циркуля-измерителя и масштабной линейки. Точки, снятые способом створов, наносят на план при помощи циркуля-измерителя и масштабной линейки. Построенный в карандаше план теодолитной съемки вычерчивают в туши, руководствуясь установленными условными знаками. Заключение В ходе написания работы были сделаны следующие выводы. Теодолитной съёмкой называется горизонтальная или контурная съёмка местности, которая выполняется с помощью теодолита. Теодолитом измеряются горизонтальные углы и углы наклона. Линии измеряются стальной лентой и дальномерами различных конструкций. По результатам теодолитной съёмки может быть составлении план без изображении рельефа. Для получения плана с изображением рельефа необходимо произвести нивелирование поверхности, на которой выполнялась теодолитная съёмка. Сочетание теодолитной съёмки и нивелирования поверхности целесообразно применять для получения плана строительного участка. Процесс теодолитной съёмки складывается из следующих видов работ: проложение теодолитных ходов, привязка их к пунктам геодезической сети, съёмка ситуации. Список использованной литературы 1. Кулешов Д.А., Г.Е. Стрельников. Инженерная геодезия для строителей, 1990г. . Ворошилов А.П. Спутниковые системы и электронные тахеометры: Учебное пособие. Челябинск: АКСВЕЛЛ, 2007. 3. Южанинов В.С. Картография с основами топографии. Учеб. - М.: Высшая школа, 2001. . Геодезические работы в землеустройстве / Маслов А.В., Горохов Г.И., Ктиторов Э.М., Юнусов А.Г. - М.: Недра, 1976. . Инженерная геодезия: учеб. пособие. / С.В. Смолич, А.Г. Верхотуров, В.И. Савельева. - Чита: ЧитГУ, 2009. 6. Куштин И.Ф., Куштин В.И. Инженерная геодезия: Учебник. - Ростов на Дону: Феникс, 2002. |
