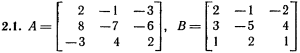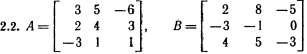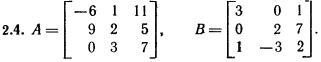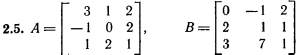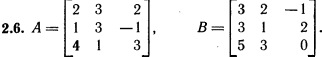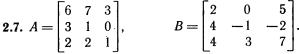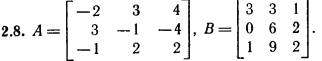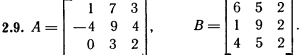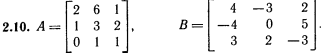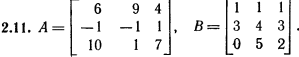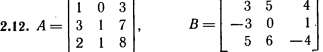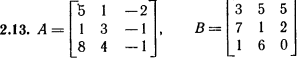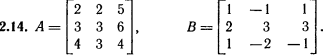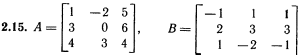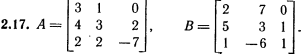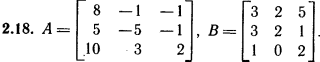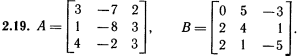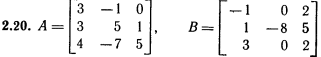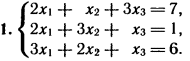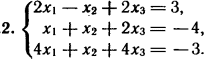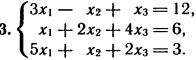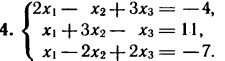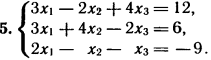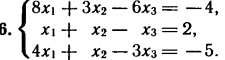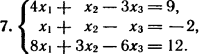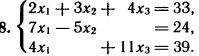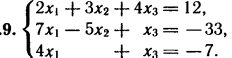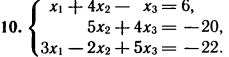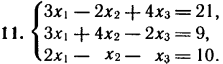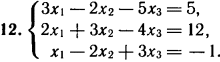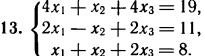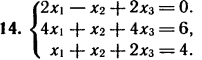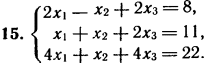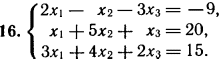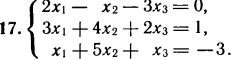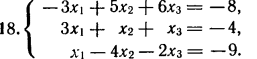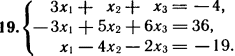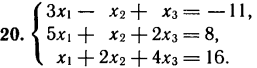Лабаратораня 4. Лаб работа №2 Действия с матрицами. Лабораторная работа Действия над матрицами

• Название: Лабораторная работа Действия над матрицами
• Анкор: Лабаратораня 4
• Дата: 25.09.2022
• Размер: 0.52 Mb.
• Имя файла: Лаб работа №2 Действия с матрицами.doc
• Тип: Лабораторная работа; #696135

Лабораторная работа № 2. Действия над матрицами.

Цель: изучить действия с массивами (матрицами) в Excel. Изучить решение систем линейных алгебраических уравнений методом обратной матрицы в Excel.

Теоретико-практический материал

Работа с массивами
Под массивом в Excel понимается диапазон ячеек, обрабатываемый единообразно.

Под формулой массива понимается единственная формула, связанная со всеми ячейками массива. Для ввода формулы массива следует:

• 
  выделить массив (ячейку или прямоугольный диапазон ячеек), для которого будет применяться формула;
  
• 
  ввести формулу;
  
• 
  нажать комбинацию клавиш 〈Shift〉 + 〈Ctrl〉 + 〈Enter〉 .
  

Пример вычисления суммы двух матриц.

Заполним две группы ячеек размером 3х3 произвольными числами (на рисунке это массивы B2:D4 и F2:H4).

Для того, чтобы результат их суммирования был записан в соответствующих ячейках J2:L4 выполним следующее:

1. 
   выделим ячейки J2:L4;
   
2. 
   в строке формул введем выражение =B2:D4+F2:H4 (вместо ручного ввода диапазона ячеек, например B2:D4, их можно просто выделить курсором на рабочем листе);
   
3. 
   после нажатия комбинации клавиш 〈Shift〉 + 〈Ctrl〉 + 〈Enter〉 формула окажется заключенной в фигурные скобки {=B2:D4+F2:H4}, что является явным признаком формулы массива и осуществится вычисление всех значений новой матрицы.
   

Произведение двух уже имеющихся квадратных матриц А и В 33 можно найти, используя встроенную функцию Excel МУМНОЖ(массив1,массив2) – функция произведения двух массивов.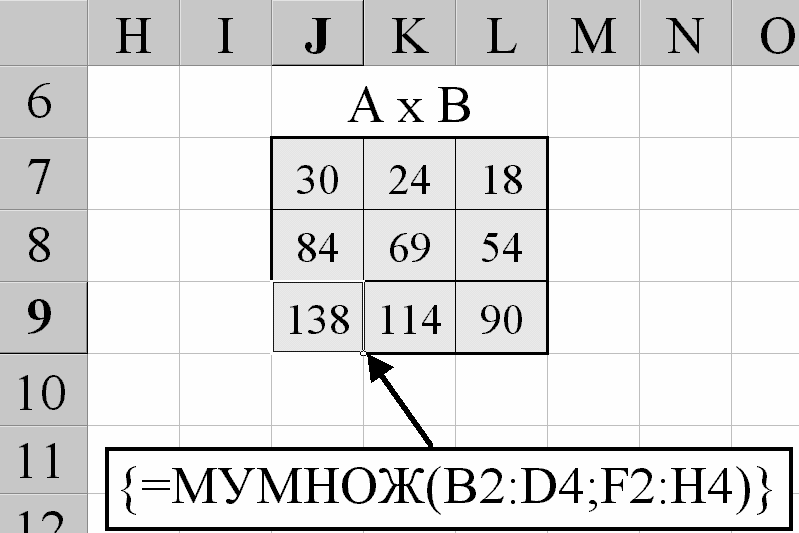


Для этого в любом месте рабочего листа необходимо

1) выделить диапазон ячеек 33 (на рисунке - это диапазон J7:L9), куда будет помещен результат вычислений;

2) вызвать функцию МУМНОЖ и на запрос Мастера Функций последовательно ввести диапазон ячеек для матриц А и В;

3) нажать комбинацию клавиш 〈Shift〉 + 〈Ctrl〉 + 〈Enter〉.
При вычислении произведения двух неквадратных матриц следует помнить, что число столбцов (n) первой матрицы mn должно совпадать с числом строк второй матрицы (nk), а размер матрицы-произведения есть mk, где m – число строк и k - число столбцов.
Вычисление обратной матрицы осуществляется аналогично с применением встроенной функции МОБР, пример вычисления приведен на рисунке. Следует помнить, что обратная матрица определена только для квадратных матриц.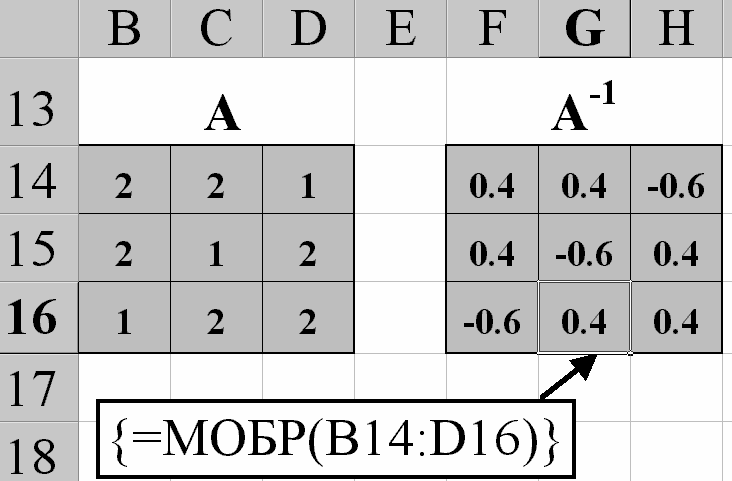

Решение системы линейных алгебраических уравнений методом обратной матрицы.
Рассматриваем систему линейных уравнений, в которой число неизвестных равно числу уравнений и решение может быть записано в матричном виде: X = A^-1 C.

Пусть дана система уравнений
10x₁+ x₂ + x₃ = 12

2 x₁ + 10 x₂ + x₃= 13

2 x₁ + 2 x₂ +10 x₃ = 14.

Она представляется в матричном виде как уравнение A  X = C, где А – матрица коэффициентов, Х – столбец неизвестных, а С – столбец свободных членов за знаком равно.

1. 
   Введите массивы коэффициентов и свободных членов.
   
2. 
   В свободном месте электронной таблицы выделите блок ячеек, совпадающий по размеру с массивом коэффициентов.
   
3. 
   Обратитесь к функции МОБР. На запрос «Мастера функций» введите адрес массива коэффициентов и завершите ввод формулы нажатием комбинации клавиш 〈Shift〉 + 〈Ctrl〉 + 〈Enter〉.
   
4. 
   Выделенные ячейки заполнятся числами. Полученная матрица и есть обратная матрица коэффициентов.
   
5. 
   В свободном месте электронной таблицы выделите блок ячеек, необходимый для размещения решений системы (в примере ячейки H18:H20).
   
6. 
   Обратитесь к функции МУМНОЖ. На запрос «Мастера функций» введите адрес обратной матрицы (F13:H15) и адрес вектора свободных членов (J7:J9), завершите ввод формулы нажатием комбинации клавиш 〈Shift〉 + 〈Ctrl〉 + 〈Enter〉 .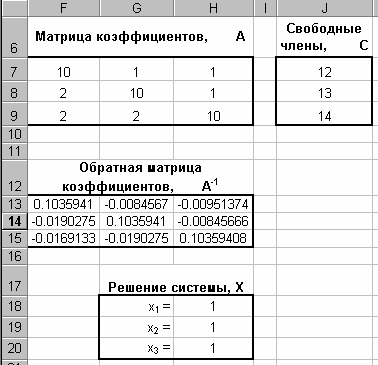
   

7. 
   Полученные значения есть решение системы уравнений.
   

Убедитесь, что функция МОБР может быть вложена как один из аргументов функции МУМНОЖ, что позволяет ввести окончательную формулу решения непосредственно в ячейки H18:H20 без промежуточного вывода обратной матрицы в ячейки F13:H15: {= МУМНОЖ (МОБР (F7:H9);J7:J9)}.

Задание для самостоятельного решения.

1. Вычислите сумму и произведение двух матриц А и В.

	2.

2. Решите систему линейных уравнений методом обратной матрицы.