ирр. Лаба+1-1. Лабораторная работа 13 по физике " Определение момента инерции твёрдых тел методом трифилярного подвеса"
 Скачать 178.5 Kb. Скачать 178.5 Kb.
|
Находим средний результат измерения по формуле: Находим средний период колебаний: n Результаты расчетов заносим в таблицу:
Рассчитаем момент инерции пустой платформы: J0=m·g·h· где h=0,00347 м – высота подъема платформы при повороте на угол a0, определяем с помощью индикатора с точностью до 1,0·10-2мм. g=9,81м/с² ‑ ускорение свободного падения π=3,14; a0=π/2 – угол поворота платформы m=0,417кг – масса платформы J0=0,417·9,81·0,00347·((4,55)²)/(2·(3,14·(3,14/2))²)=0,025кг·м²; нагруженной платформы Jсист по формуле: Jсист=mсист·g·h· диска, кольца и параллелепипеда по формуле: JT=Jсист- J0, кг·м²; Диск Jсист=((0,417+1,103)·9,81·0,0027·(2,37)²)/(2·((3,14·(3,14/2))²)=0,056 кг·м² JT=Jсист-J0=0,056-0,025=0,031 кг·м²; Кольцо Jсист=((0,417+1,103)·9,81·0,0027·(2,97)²)/(2·((3,14·(3,14/2))²)=0,01064 кг·м²; JT=Jсист-J0=0,0073-0,025=0,012 кг·м²; Параллелепипед Jсист=((0,417+0,425)·9,81·0,0028·(2,88)²)/( 2·((3,14·(3,14/2))²)=0,11кг·м² JT=Jсист-J0=0,11-0,025=0,085кг·м²;
Рассчитываем абсолютную и относительную погрешности измерения: tp,N=2,8 tp,=2,0-соответствующие коэффициенты Стьюдента при N=5(доверительная вероятность 95%) =0,01-точность секундомеров Определение момента инерции тел теоретическим путём Пустая платформа:
Параллелепипед:
=(a1+a2+a3+a4+a5)/5=0,1536 м
=(b1+b2+b3+b4+b5)/5=0,122 м Диск:
Кольцо: Rвнеш:
rвнутр:
Обработка результатов эксперимента Статистическая обработка результатов прямых измерений. Определяем абсолютную погрешность Δt измерения времени 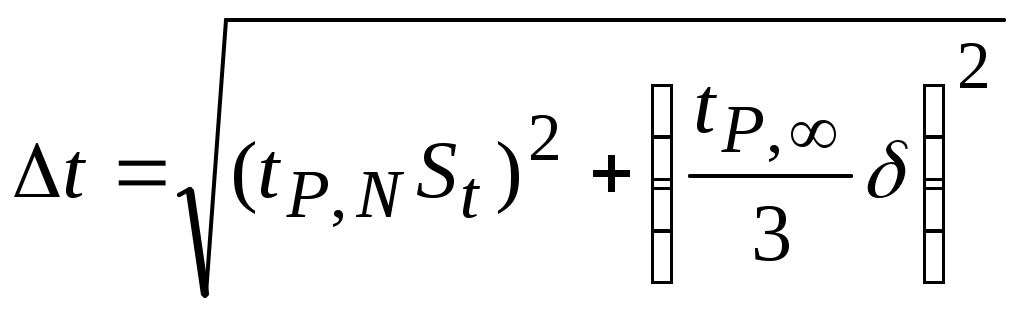 Определяем относительную погрешность εt измерения времени для каждого тела: εt=∆t/<t>, Пустая платформа St =√ ((139,2-136,5)²+(136,2-136,5)²+(134,2-136,5)²)/ 3*(3-1)=0,59; εt=(2,6/136,5)=0,019; εt= 1,9% Диск St=√ ((73,1-71,2)²+(70,4-71,2)²+(70,1-71,2)²)/ 3*(3-1)=0,42; εt=1,8/71,2=0,025 εt= 2,5% Параллелепипед St=√ ((84,6-84,6)²+(87,8-84,6)²+(86,8-84,6)²)/3*(3-1)=0,65; εt=(2,8/84,6)=0,033; εt= 3,3% Кольцо St=√ ((90,7-88,9)²+(88,8-88,9)²+(87,5-88,9)2)/3*(3-1)=0,47; εt=2,1/88,9=0,023; εt=2,3%
4.Статистическая обработка результатов косвенных измерений. Определяем относительную погрешность εT измерения периода колебаний: εT=√εt²+εn², где εn – относительная погрешность измерения числа полных колебаний n εn=∆n/<n>, n1=139,2/30=4.64 n2=136,2/4.64=29.4 n3=134,2/4.64=29.8 ∆n=t*Sn , Sn=√∑(ni-‹n›)2/N*(N-1) Sn=√2*(30-29,4)2+(29,8-29,4)2/3*(3-1)=0,005 ∆n=4,3*0,005=0,02 εn=0,02/29,4=0,0007 Определяем абсолютную погрешность ∆T измерения периода колебаний: ∆T=εT·<T>, с εT=√εt²+εn², Пустая платформа :εT=√(0,019)²+(0,0007)²=0,019; ∆T=0,019*4,55=0,09 с; Диск:εT=√(0,025)²+(0,025)²=0,04; ∆T=0,04*2,37=0,09 с; Кольцо: εT=√(0,023)²+(0,023)²=0,057; ∆T=0,057*2,97=0,17с; Параллелепипед: εT=√(0,023)²+(0,023)²=0,03; ∆T=0,03*2,88=0,09 с; Определяем относительную и абсолютную погрешности полученного экспериментального момента инерции платформы: εm=∆m/m=0,001/0,417=0,0024; εh=∆h/ εJ0=√(0,0024)²+(2*0,019)²+(0,03)²=0,073 ; εJ0=7,3% ∆J0= J0· εJ0, кг·м² ∆J0=0,025·0,073=0,00322кг·м²; Аналогично определяем относительную и абсолютную погрешности момента инерции системы (платформы с телом). εJсист=√εmсист²+εh²+(2*εT)² εh=∆h/ Определяем относительную погрешность измерения высоты подъема нагруженной платформы: ∆h=k*Sh, где k – соответствующий коэффициент Стьюдента; k=2,8 Sh – среднеквадратичное отклонение. Sh=√∑(hi-‹ h ›)2/N’*(N’-1) где N’=5 - количество измерений высоты подъема системы. ∆Jсист= Jсист* εJсист,кг·м² Диск Sh=0,000038 ∆h=k*Sh=2,8*0,000038=0,0001 εh=∆h/ εJсист=√(0,001/(0,417+1,103))²+0,037²+(2*0,025)²=0,16 ∆Jсист=0,031*0,16=0,0049 кг·м² Кольцо εJсист=√(0,001/(0,417+1,103))²+0,037²+(2*0,023)²=0,5 ∆Jсист=0,012*0,5=0,0056 кг·м² Параллелепипед εJсист=√(0,001/(0,417+0,425))2+ 0,042²+(2*0,023)²=0,3 ∆Jсист=0,085*0,3=0,002 кг·м² Определяем относительную и абсолютную погрешности момента инерции тела. ∆Jт=√(∆J0)²+( ∆Jсист)² , кг·м² εJт=∆Jт/Jт Диск ∆Jт=√(0,00322)²+(0,0049)²=0,044 кг·м² εJт=(0,044/0,031)*100%=1,4% Кольцо ∆Jт=√(0,00322)²+(0,0056)²=0,051 кг·м² εJт=(0,051/0,012)*100%=4,25% Параллелепипед ∆Jт=√(0,00322)²+(0,002)²=0,04 1кг·м² εJт=(0,041/0,085)*100%=1,48% Определение абсолютной и относительной погрешности. Параллелепипед εJT(теор)=√(∆m/m)²+[∆(<b>²+<c>²)/(<b>²+<c>²)]² , инстр. Погр=0.01 мм где ∆(²+ ∆b=k*Sb Sb=√∑(bi-<b>)2/N’*(N’-1) Sb=√2*(0,121-0,122)2+(0,123-0,122)2/5*(5-1)=0,00004 ∆b=2,8*0,00004=0,0001 ∆c= k*Sc Sc=√∑(ci-<c>)2/N’*(N’-1) Sc=√2*(0,048-0,049)2/5*(5-1)=0,00003 ∆c=2,8*0,00003=0,00008 ∆(²+ εJT(теор)=(√(0,001/0,425)²+(0,00004/(0,0138+0,002)²)*100%=0,19 % ∆Jпарал. (теор)= εJT(теор)* Jпарал ∆Jпарал. (теор)=0,19*0,00225=0,43 Пустая платформа εJ(теор)=√ (∆m/ m )²+ [ ∆R²/<R>²]² εJ(теор)=(√ (0,001/0,417)²+(0,0001²/0,15012)²)*100%=0,4% ∆Jплатф (теор)= εJT(теор)* Jпл(теор)=0,4%*0,0045=1,8 Диск εJ(теор)=√ (∆m/<m>)²+ [ ∆R² / <R>² ]² εJ(теор)=(√ (0,001/1,103)2+(0,0001²/0,0543²)²)*100%=0,07 % ∆Jдиск (теор)= εJT(теор)* Jдиск(теор)=0,07%*0,0068=0,49 Кольцо εJ(теор)=√ (∆m/<m>)²+ [∆(<r>²+<R>²)/(<r>²+<R>²)]² ∆( ∆( εJ(теор)=(√(0,001/1,103)2+(0,00007)/(0,0013+0,0027)²)*100%=0,03% ∆Jкол (теор)= εJT(теор)* Jкол(теор)=0,03%*0,00157=0,047 Результаты расчетов сведем в таблицу:
Вывод: Мы экспериментально и теоретически определили момент инерции параллелепипеда, кольца и диска. При сравнении практических и теоретических значений мы обнаружили, что практические результаты оказались завышенными, правда в пределах погрешностей. Это объясняется тем, что на платформу с телом, при крутильных колебаниях, действовали неучтенные нами силы трения и сопротивления воздуха. |

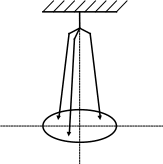 В нашей работе момент инерции тела определяется при помощи трифилярного повеса (рис. 1), который представляет собой круглую платформу, подвешенную на
В нашей работе момент инерции тела определяется при помощи трифилярного повеса (рис. 1), который представляет собой круглую платформу, подвешенную на 
