ЛР 1.1. Определение фокусного расстояния линз. Лабораторная работа 1 Определение фокусных расстояний собирающей и рассеивающей линз по методу Бесселя Владивосток
 Скачать 103 Kb. Скачать 103 Kb.
|
|
Дальневосточный федеральный университет Кафедра общей физики ЛАБОРАТОРНАЯ РАБОТА № 1.1 Определение фокусных расстояний собирающей и рассеивающей линз по методу Бесселя Владивосток Цель работы: изучение свойств собирающих и рассеивающих линз и их систем, ознакомление с методом Бесселя, определение фокусного расстояния линзы. Краткая теория Линзой называется прозрачное для света тело, ограниченное двумя сферическими поверхностями. Основные виды линз представлены на рис.1.  Собирающие (в воздухе): 1 – двояковыпуклая линза, 2 – плоско-выпуклая линза, 3 – вогнуто-выпуклая линза. Рассеивающие (в воздухе): 4 – двояковогнутая линза, 5 – плоско-вогнутая линза, 6 – выпукло-вогнутая линза. Тонкой называется линза, толщина которой намного меньше любого из ее радиусов кривизны. Оптическая система называется центрированной, если центры кривизны всех ее преломляющих поверхностей лежат на одной прямой, называемой главной оптической осью системы. Точка пересечения плоскости линзы с оптической осью называется оптическим центром тонкой линзы. Любая прямая, проходящая через оптический центр линзы и не совпадающая с главной оптической осью, называется побочной оптической осью. Если на собирающую линзу падают лучи, параллельные главной оптической оси, то они, после преломления в линзе, пересекаются в одной точке, лежащей на главной оптической оси и называемой главным фокусом линзы F (рис. 2). У линзы имеется два главных фокуса по обе стороны от нее. Расстояние f от оптического центра до фокуса называется фокусным расстоянием. Если радиусы кривизны поверхностей линзы одинаковы и с обеих сторон от линзы среда одна и та же, то фокусные расстояния линзы одинаковы. 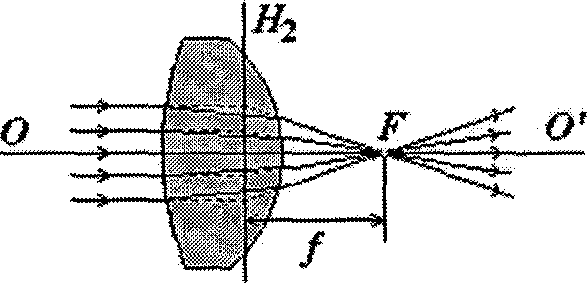 Рис. 2. Ход лучей в собирающей линзе. Если на рассеивающую линзу падают лучи, параллельные главной оптической оси, то в одной точке, также называемой главным фокусом, пересекаются не сами преломленные лучи, а их продолжения (рис.3). Фокус в этом случае называется мнимым, а фокусное расстояние считается отрицательным. У рассеивающей линзы также два главных фокуса по обе стороны от нее.  Рис. 3. Ход лучей в рассеивающей линзе. Плоскость, проходящая через главный фокус линзы перпендикулярно главной оптической оси, называется фокальной плоскостью, а точка пересечения какой-либо побочной оси с фокальной плоскостью называется побочным фокусом. Если на линзу падает пучок лучей, параллельных какой-то побочной оси, то после преломления либо сами лучи, либо их продолжения (в зависимости от вида линзы) пересекаются в соответствующем побочном фокусе. Лучи, идущие через оптический центр тонкой линзы, своего направления практически не меняют. Построение изображения в линзах. Для построения изображения светящейся точки из этой точки надо взять не менее двух лучей, падающих на линзу, и построить ход этих лучей. Как правило, выбираются лучи, параллельные главной оптической оси, проходящие через главный фокус линзы, или идущие через оптический центр линзы. Пересечение этих лучей, либо их продолжений, дает действительное или мнимое изображение точки. Для получения изображения отрезка строят изображения его крайних точек. Если светящийся предмет – небольшой отрезок, перпендикулярный главной оптической оси, то его изображение тоже будет представляться отрезком, перпендикулярным главной оптической оси. Проще всего построить изображение отрезка, одна из двух крайних точек которого лежит на главной оптической оси: в этом случае строится изображение другой его крайней точки и опускается перпендикуляр на главную оптическую ось (рис. 4). Для построения изображений также могут быть использованы побочные оптические оси и побочные фокусы. В зависимости от вида линзы и положения предмета относительно линзы изображение может быть увеличенным или уменьшенным. При построении изображений используют условные изображения тонкой линзы: ↕ - двояковыпуклая линза, ↕ - двояковогнутая линза  Рис. 4а. Построение действительного изображения в тонкой собирающей линзе (предмет находится за фокусом). 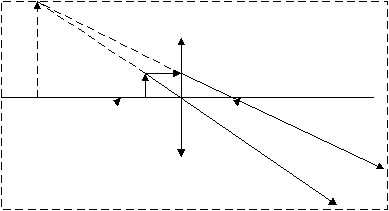 Рис. 4б. Построение мнимого изображения в тонкой собирающей линзе (предмет находится между фокусом и линзой). 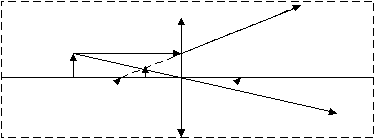 Рис. 4в. Построение мнимого изображения в тонкой рассеивающей линзе (предмет находится за фокусом). Формула линзы. Если обозначить расстояние от предмета до линзы – s, а расстояние от линзы до изображения - s′, то формулу тонкой линзы можно записать в виде: где R1 и R2 – радиусы кривизны сферических поверхностей линзы, n1 – показатель преломления вещества, из которого сделана линза, n2 – показатель преломления среды, в которой находится линза. Величина D, обратная фокусному расстоянию линзы, называется оптической силой линзы и измеряется в диоптриях. У собирающей линзы оптическая сила положительна, у рассеивающей – отрицательна. Другой важный параметр линзы – линейное увеличение Г. Оно показывает, чему равно отношение линейного размера изображения h′ к соответствующему размеру предмета h. Можно показать, что Г=h′/h=s′/s. Недостатки изображения в линзе. Сферическая аберрация приводит к тому, что изображение точки получается неточечным, а в виде небольшого кружка. Этот недостаток связан с тем, что лучи, прошедшие через центральную область линзы и лучи, прошедшие через ее края, собираются не в одной точке. Хроматическая аберрация наблюдается при прохождении через линзу сложного света, содержащего волны разной длины. Показатель преломления зависит от длины волны. Это приводит к тому, что края изображения имеют радужную окраску. Астигматизм – это дефект изображения, связанный с зависимостью фокусного расстояния от угла падения света на линзу. Это приводит к тому, что изображение точки может иметь вид кружка, эллипса, отрезка. Дисторсия – это недостаток изображения, который имеет место, если поперечное увеличение предмета линзой в пределах поля зрения неодинаково. Если увеличение убывает от центра к периферии, имеет место бочкообразная дисторсия, а если наоборот – то подушкообразная дисторсия. Недостатки изображения стремятся устранить или уменьшить путем подбора системы линз. Теория метода. Удобным методом определения фокусного расстояния линзы является метод Бесселя. Он заключается в том, что при достаточно большом расстоянии L между предметом и экраном можно найти два положения линзы, при которых получается четкое изображение предмета – в одном случае увеличенное, в другом – уменьшенное. Эти положения можно найти, решая систему из двух уравнений: s′ + s = L и 1/ s′ + 1/ s = 1/f. Выразив s′ из первого уравнения, и подставив полученное выражение во второе, получим квадратное уравнение, решение которого можно записать: Так как дискриминант этого уравнения должен быть больше нуля: L2 – 4Lf≥0, то L≥4f – только при таком условии можно получить два четких изображения предмета. Из формулы (1) следует, что существует два положения линзы, дающих четкое изображение предмета, симметрично расположенных относительно центра отрезка между предметом и экраном. Расстояние r между этими положениями можно найти из формулы: Если из данной формулы выразить фокусное расстояние линзы, то получим: Фокусное расстояние рассеивающей линзы так определить нельзя, т.к. она не дает действительных изображений предмета. Но если рассеивающую линзу сложить с более сильной собирающей линзой, то получится собирающая система линз. Фокусные расстояния системы и собирающей линзы можно найти по методу Бесселя, а фокусное расстояние рассеивающей линзы определить затем из соотношения: 1/fΣ=1/f+ + 1/f- , откуда следует: Лабораторная установка Лабораторная установка включает в себя оптическую скамью стержневого типа. Линзы в оправах размещаются между стержнями и могут перемещаться вдоль них. Для отсчета расстояния служит рулетка. Для имитации светящегося предмета используется двумерная дифракционная решетка (центральная зона объекта МОЛ-1), освещаемая лазером. Изображении е на экране представляет собой крестообразную фигуру, состоящую из ярких пятен. Внешний вид установки представлен на рис. 5. 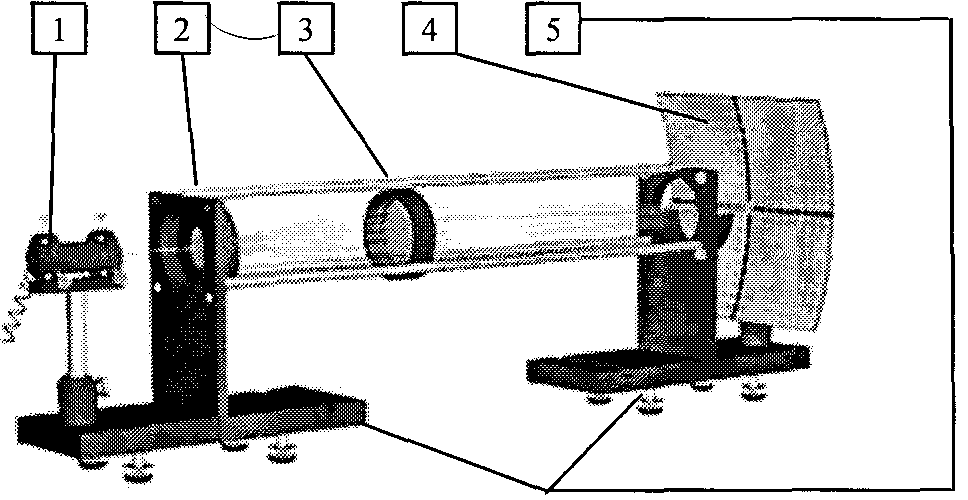 1 – лазер, 2 – дифракционная решетка, 3 – линза, 4 – экран, 5 – оптическая скамья. Рис.5. Установка для определения фокусного расстояния линзы. Порядок выполнения работы
(4). Посчитать погрешность измерения.
Таблица
Контрольные вопросы
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
