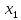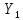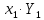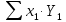Лабораторная работа № 1 Планирование эксперимента. Лабораторная работа 1. Лабораторная работа 1 Планирование эксперимента
 Скачать 32.12 Kb. Скачать 32.12 Kb.
|
|
Лабораторная работа № 1 Планирование эксперимента Цель работы: Научится применять методы планирования эксперимента для повышения эффективности эксперимента. Составить полнофакторный план для своего исследования. Получить уравнение регрессии. Планирование эксперимента (англ. experimental design techniques) — комплекс мероприятий, направленных на эффективную постановку опытов. Основная цель планирования эксперимента — достижение максимальной точности измерений при минимальном количестве проведенных опытов и сохранении статистической достоверности результатов. Методы планирования эксперимента позволяют минимизировать число необходимых испытаний, установить рациональный порядок и условия проведения исследований в зависимости от их вида и требуемой точности результатов. Если же по каким-либо причинам число испытаний уже ограничено, то методы дают оценку точности, с которой в этом случае будут получены результаты. Методы учитывают случайный характер рассеяния свойств испытываемых объектов и характеристик используемого оборудования. Они базируются на методах теории вероятности и математической статистики. Планирование эксперимента включает ряд этапов: 1. Установление цели эксперимента (определение характеристик, свойств и т. п.) и его вида (определительные, контрольные, сравнительные, исследовательские). 2. Уточнение условий проведения эксперимента (имеющееся или доступное оборудование, сроки работ, финансовые ресурсы, численность и кадровый состав работников и т. п.). Выбор вида испытаний (нормальные, ускоренные, сокращенные в условиях лаборатории, на стенде, полигонные, натурные или эксплуатационные). 3. Выявление и выбор входных и выходных параметров на основе сбора и анализа предварительной (априорной) информации. Входные параметры (факторы) могут быть детерминированными, то есть регистрируемыми и управляемыми (зависимыми от наблюдателя), и случайными, то есть регистрируемыми, но неуправляемыми. Наряду с ними на состояние исследуемого объекта могут оказывать влияние нерегистрируемые и неуправляемые параметры, которые вносят систематическую или случайную погрешность в результаты измерений. Это — ошибки измерительного оборудования, изменение свойств исследуемого объекта в период эксперимента, например, из-за старения материала или его износа, воздействие персонала и т. д. 4. Установление потребной точности результатов измерений (выходных параметров), области возможного изменения входных параметров, уточнение видов воздействий. Выбирается вид образцов или исследуемых объектов, учитывая степень их соответствия реальному изделию по состоянию, устройству, форме, размерам и другим характеристикам. На назначение степени точности влияют условия изготовления и эксплуатации объекта, при создании которого будут использоваться эти экспериментальные данные. Условия изготовления, то есть возможности производства, ограничивают наивысшую реально достижимую точность. Условия эксплуатации, то есть условия обеспечения нормальной работы объекта, определяют минимальные требования к точности. Точность экспериментальных данных также существенно зависит от объёма (числа) испытаний — чем испытаний больше, тем (при тех же условиях) выше достоверность результатов. Для ряда случаев (при небольшом числе факторов и известном законе их распределения) можно заранее рассчитать минимально необходимое число испытаний, проведение которых позволит получить результаты с требуемой точностью. 5. Составление плана и проведение эксперимента — количество и порядок испытаний, способ сбора, хранения и документирования данных. Порядок проведения испытаний важен, если входные параметры (факторы) при исследовании одного и того же объекта в течение одного опыта принимают разные значения. Например, при испытании на усталость при ступенчатом изменении уровня нагрузки предел выносливости зависит от последовательности нагружения, так как по-разному идет накопление повреждений, и, следовательно, будет разная величина предела выносливости. В ряде случаев, когда систематически действующие параметры сложно учесть и проконтролировать, их преобразуют в случайные, специально предусматривая случайный порядок проведения испытаний (рандомизация эксперимента). Это позволяет применять к анализу результатов методы математической теории статистики. Порядок испытаний также важен в процессе поисковых исследований: в зависимости от выбранной последовательности действий при экспериментальном поиске оптимального соотношения параметров объекта или какого-то процесса может потребоваться больше или меньше опытов. Эти экспериментальные задачи подобны математическим задачам численного поиска оптимальных решений. Наиболее хорошо разработаны методы одномерного поиска (однофакторные однокритериальные задачи), такие как метод Фибоначчи, метод золотого сечения. 6. Статистическая обработка результатов эксперимента, построение математической модели поведения исследуемых характеристик. Необходимость обработки вызвана тем, что выборочный анализ отдельных данных, вне связи с остальными результатами, или же некорректная их обработка могут не только снизить ценность практических рекомендаций, но и привести к ошибочным выводам. Обработка результатов включает: - определение доверительного интервала среднего значения и дисперсии (или среднего квадратичного отклонения) величин выходных параметров (экспериментальных данных) для заданной статистической надежности; - проверка на отсутствие ошибочных значений (выбросов), с целью исключения сомнительных результатов из дальнейшего анализа. Проводится на соответствие одному из специальных критериев, выбор которого зависит от закона распределения случайной величины и вида выброса; - проверка соответствия опытных данных ранее априорно введенному закону распределения. В зависимости от этого подтверждаются выбранный план эксперимента и методы обработки результатов, уточняется выбор математической модели. Построение математической модели выполняется в случаях, когда должны быть получены количественные характеристики взаимосвязанных входных и выходных исследуемых параметров. Это — задачи аппроксимации, то есть выбора математической зависимости, наилучшим образом соответствующей экспериментальным данным. Для этих целей применяют регрессионные модели, которые основаны на разложении искомой функции в ряд с удержанием одного (линейная зависимость, линия регрессии) или нескольких (нелинейные зависимости) членов разложения (ряды Фурье, Тейлора). Одним из методов подбора линии регрессии является широко распространенный метод наименьших квадратов. Для оценки степени взаимосвязанности факторов или выходных параметров проводят корреляционный анализ результатов испытаний. В качестве меры взаимосвязанности используют коэффициент корреляции: для независимых или нелинейно зависимых случайных величин он равен или близок к нулю, а его близость к единице свидетельствует о полной взаимосвязанности величин и наличии между ними линейной зависимости. При обработке или использовании экспериментальных данных, представленных в табличном виде, возникает потребность получения промежуточных значений. Для этого применяют методы линейной и нелинейной (полиноминальной) интерполяции (определение промежуточных значений) и экстраполяции (определение значений, лежащих вне интервала изменения данных). 7. Объяснение полученных результатов и формулирование рекомендаций по их использованию, уточнению методики проведения эксперимента. Снижение трудоёмкости и сокращение сроков испытаний достигается применением автоматизированных экспериментальных комплексов. Такой комплекс включает испытательные стенды с автоматизированной установкой режимов (позволяет имитировать реальные режимы работы), автоматически обрабатывает результаты, ведет статистический анализ и документирует исследования. Но велика и ответственность инженера в этих исследованиях: четкое поставленные цели испытаний и правильно принятое решение позволяют точно найти слабое место изделия, сократить затраты на доводку и процесс проектирования. Ход работы: 1. Пропишите тему и цели вашего исследования. 2. Выявите основные входные факторы действующие при проведении вашего эксперимента и запишите их в таблицу 1. 3. Определите и запишите в таблицу 1 исходные (зависимые) факторы на которые оказывают влияние входные факторы, заданные в пункте 2. Таблица 1– Параметры полнофакторного эксперимента
4. Определите и запишите в таблицу 2 интервалы и уровни варьирования входных (управляемых) факторов. Таблица 2 – Уровни и интервалы варьирования исследуемых факторов
5. Составить план полнофакторного эксперимента заполнив таблицу 3.
6. Выполнить раcчеты по примеру Верхний уровень по концентрации массы 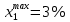 , нижний , нижний 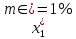 , тогда , тогда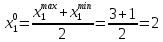 (1.1) (1.1)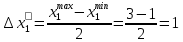 (1.2) (1.2)Верхний уровень по показателю межножевого зазора 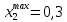 мм, нижний мм, нижний 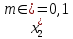 мм, тогда мм, тогда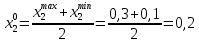 (1.3) (1.3)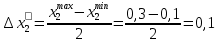 (1.4) (1.4) Линейное уравнение регрессии имеет вид: 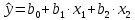 (1.5) (1.5)Любой коэффициент уравнения регрессии 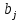 определяется скалярным произведением столбца определяется скалярным произведением столбца 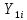 на соответствующий столбец на соответствующий столбец 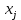 , деленным на число опытов в матрице планирования N: , деленным на число опытов в матрице планирования N: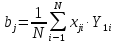 (1.6) (1.6)Для примера рассмотрим нахождение коэффициента 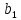 . Расчетные данные представлены в табл. 4. . Расчетные данные представлены в табл. 4.Таблица 4- Расчетные данные для коэффициента 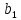
Тогда коэффициент уравнения регрессии 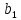 равен: равен: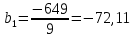 Аналогично для коэффициента 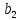 расчетные данные представлены в табл. 5. расчетные данные представлены в табл. 5.Таблица 5 -Расчетные данные для коэффициента 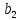
Тогда коэффициент уравнения регрессии 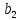 равен: равен: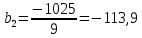 Для вычисления коэффициента 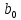 используем формулу: используем формулу: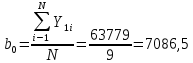 (1.7) (1.7)Таким образом, линейное уравнение регрессии для определения влияния трех факторов (скорости газа, плотность орошения жидкости, зазора между пластинами насадки) имеет вид: 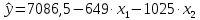 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||