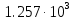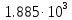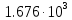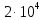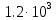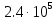ЗОНДИРУЮЩИЕ СИГНАЛЫ. Лабораторная работа 1 Простые зондирующие сигналы
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
|
ЗОНДИРУЮЩИЕ СИГНАЛЫ Лабораторная работа № 1 «Простые зондирующие сигналы » Цель работы: Исследование простого сигнала, спектра и КФ. Установить зависимость ширины спектра от и вида сигнала, а так же КФ от длительности импульса. ТЕОРИЯ Зондирующие сигналы (ЗС) в радиолокации (РЛ) определяют дальность, точность координат, скорость объекта и т.д. К простым зондирующим сигналам относятся импульсные сигналы, которые в свою очередь являются узкополосными. Рассмотрим простые зондирующие сигналы. В качестве примера простого зондирующего сигнала возьмем одиночный импульс (или пачка импульсов). Одиночный импульс (рис. 1,а) записывается следующим выражением вида: 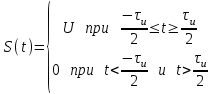 (1.1) (1.1)G(ω) R(τ) S(t)  90 от Ес   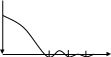   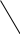  t U  0 f 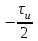 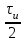 0  -τu/2 τu/2 0 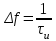 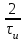 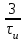 и   a) б) в) Рис 1. Одиночный импульс. Спектр сигнала и его КФ Спектр сигнала (спектральная плотность импульса) (рис. 1,б) определяется по формуле 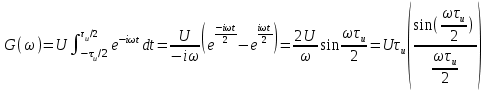 (1.2) (1.2)где 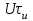 -площадь импульса, определяется при -площадь импульса, определяется при 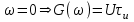 Одиночный импульс имеет сплошной спектр, а для последовательности импульсов дискретный. Спектр сигнала имеет размерность 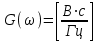 . .Полоса частот (рис. 1.б), где заключено 90% сигнала равна: 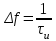 . (1.3) . (1.3)Корреляционная функция 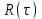 простого сигнал (рис.1,в) лежит в пределах от простого сигнал (рис.1,в) лежит в пределах от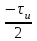 до до 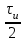 и определяется из формулы: и определяется из формулы: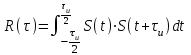 (1.4) (1.4) Корреляционная функция 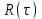 – это энергия сигнала и имеет размерность – это энергия сигнала и имеет размерность 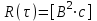 База простого сигнала 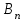 – это произведение полосы частот занимаемой спектром на его длительность: – это произведение полосы частот занимаемой спектром на его длительность: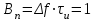 . (I.5) . (I.5)Порядок выполнения работы 1) Изменяя длительность информационного импульса 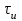 в пределах в пределах1-90 мкс определить ширину спектра сигнала 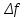 по графику спектральной плотности G() и базу сигнала по графику спектральной плотности G() и базу сигнала 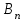 . По полученным результатам составить таблицу 1. . По полученным результатам составить таблицу 1.Таблица 1.
2) Зарисовать: а) вид сигнала; б) спектр сигнала; в) КФ сигнала 3) По полученным данным (таблица 1) в результате выполнения лабораторной работы, определить зависимость ширины и вида спектра G(), а так же КФ R() от длительности импульса и. Вопросы для защиты лабораторной работы №1. Определение зондирующего сигнала. Что такое простые сигналы? Какой вид имеет спектр G() одиночного импульса, а какой последовательности импульсов? Как зависит спектр G() и корреляционная функция R() простого сигнала от длительности импульсов? Физический смысл корреляционной функции R()? В каких пределах лежит корреляционная функция R() простого сигнала? Чему равна полоса частот простого сигнала? Что такое база 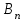 сигнала? сигнала? Чему равна база 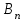 сигнала? сигнала? 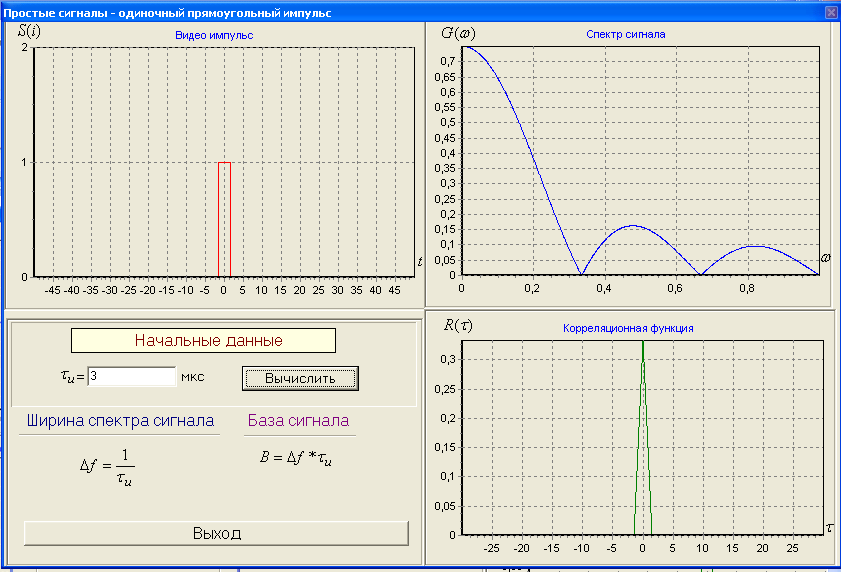 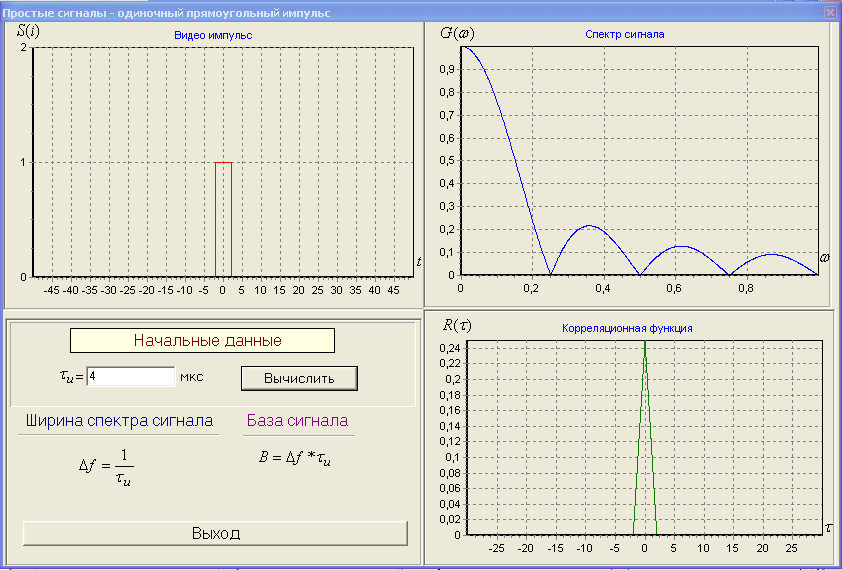 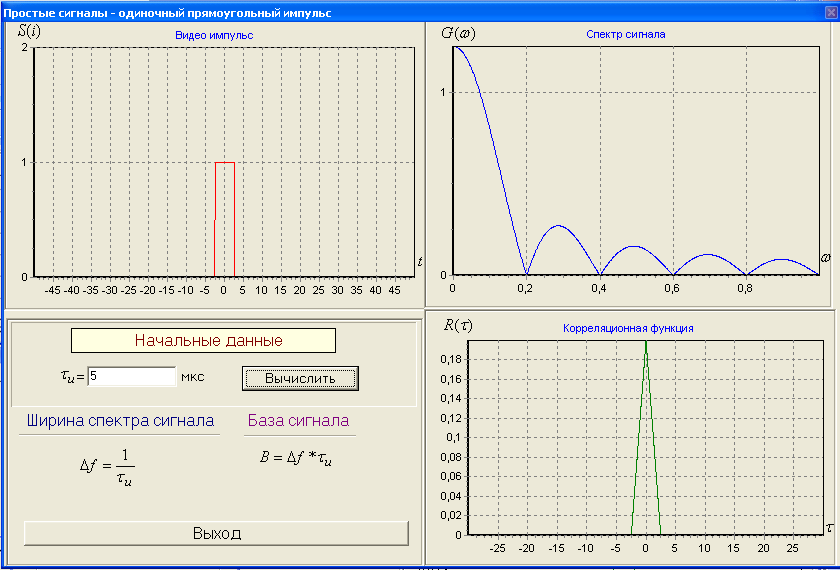 Сложные сигналы. ТЕОРИЯ .Простой информационный импульс длительностью τu разбивают на ряд импульсов одинаковой или разной длительностью (рис.2.1,а). 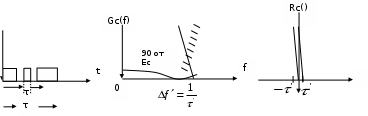 а) б) в) Рис 2.1 Cложный сигнал. Спектр сигнала и его КФ Ширина спектра сигнала G() (рис. 2.1б) будет определяться самым коротким импульсом длительностью τ, а корреляционная функция R() (рис. 2.1,в) будет лежать в пределах от -τ до τ . Полоса частот, где заключено 90% энергии сигнала равна (рис.2.1,б): 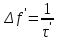 . (2.1) . (2.1)Поскольку энергия по отношению к простому сигналу не изменилась то корреляционная функцияR() (рис.2.1,в), для сохранения своей площади по отношению к простому сигналу будет лежать выше простого сигнала. База сложного сигнала 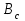 будет равна: будет равна: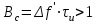 . (2.2) . (2.2)В большинстве случаев большой интерес представляют сигналы с Базой равной много больше 1. 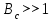 . (2.3) . (2.3)Выражение (2.3) определяет собой широкополосный шумоподобный сигнал (ШШС). У такого сигнала структура его приближается к белому шуму, а корреляционная функция стремиться к дельта функции, т.е. стремиться в бесконечность. В качестве сложных сигналов могут выступать и сигналы линейной частотной модуляции (ЛЧМ) и коды Баркера В 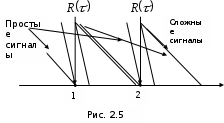 ыводы: переход от простых к сложным сигналам позволяет обострить корреляционную функцию ыводы: переход от простых к сложным сигналам позволяет обострить корреляционную функцию 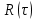 , а это значит, что можно существенно улучшить различение, разрешение и распознавания цели, т.е. , а это значит, что можно существенно улучшить различение, разрешение и распознавания цели, т.е. Как видно из рис. 2.5 зондирующий сигнал надо брать с острыми корреляционными функциями 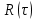 (сложные сигналы), так как легче произвести различие, разрешение, измерение и т.д. (сложные сигналы), так как легче произвести различие, разрешение, измерение и т.д.Вот почему выгоднее брать зондирующие сигналы не простые, а сложные Лабораторная работа № 2 «Сигналы с Линейной частотной модуляцией (ЛЧМ)» Цель работы: Исследование ЛЧМ-сигнала, его спектра и КФ ТЕОРИЯ 2.1 ЛЧМ-сигнал ЛЧМ-сигнал представляет собой радиоимпульс с длительностью 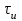 и частотой заполнения радиоимпульса с длительностью τu которая изменяется по закону и частотой заполнения радиоимпульса с длительностью τu которая изменяется по закону 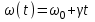 где где 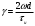 - скорость нарастания частоты при - скорость нарастания частоты при 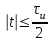 . Полная фаза (при φ=0) есть: . Полная фаза (при φ=0) есть: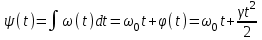 . (2.4) . (2.4)ЛЧМ-сигнал представляется выражением (Рис. 2.2) S(t) 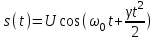 . (2.5) . (2.5)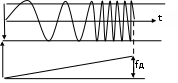 f(t)  t Рис.2.2 ЛЧМ-сигнал 2.2 Спектр ЛЧМ Спектр ЛЧМ-сигнала определяется выражением: 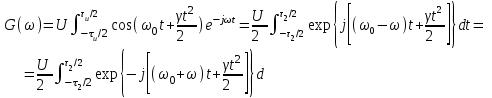 (2.6) (2.6)С учетом всех преобразований окончательная формула для спектра ЛЧМ-сигнала будет. 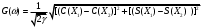 , (2.7) , (2.7)где 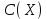 и и 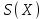 - интегралы Френеля - интегралы Френеля 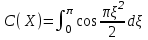 ; ; 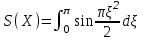 ; (2.8) ; (2.8)а 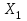 и и 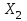 равны: равны: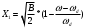 ; ; 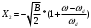 . (2.9) . (2.9)где B- база ЛЧМ-сигнала: 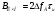 (2.10) (2.10)На рис. 2.3 представлены спектры сигналов при разных значениях их базы 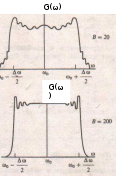 Рис. 2.3 Спектры ЛЧМ-сигналов при различных значениях базы 2.3 КФ ЛЧМ-сигнала. Корреляционная функция ЛЧМ-сигнала определяют по формуле: 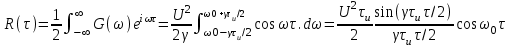 (2.11) (2.11)График нормированной КФ и ее огибающей, имеющую лепестковую структуру представлены на рис. 2.4. 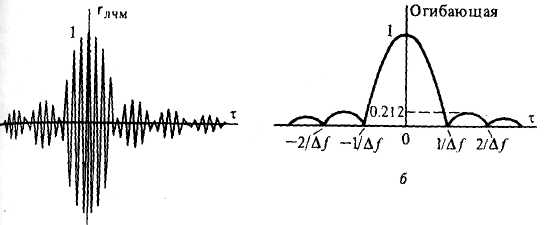 Рис 2.4 Нормированная КФ и огибающая ЛЧМ-сигнала Рис 2.4 Нормированная КФ и огибающая ЛЧМ-сигналаФормула (2.11) устанавливает следующее свойство ЛЧМ-сигнала: ширина главного лепестка огибающей КФ обратно пропорциональна девиации частоты fд импульса и. Это объясняется тем, что огибающая первый раз обращается в нуль при сдвиге сигнала относительно его копии на интервал времени  . Применяемые в радиолокации ЛЧМ-сигналы характеризуются значительной девиацией частоты, поэтому главный лепесток КФ весьма узкий. На ряду с достоинствами ЛЧМ-сигнала, существует и недостаток а именно: высота двух первых лепестков АКФ достаточно велика, и составляет 0.212 от высоты центрального лепестка. Что при значительных уровнях шумов это может привести к ошибочному определению временного положения импульса. . Применяемые в радиолокации ЛЧМ-сигналы характеризуются значительной девиацией частоты, поэтому главный лепесток КФ весьма узкий. На ряду с достоинствами ЛЧМ-сигнала, существует и недостаток а именно: высота двух первых лепестков АКФ достаточно велика, и составляет 0.212 от высоты центрального лепестка. Что при значительных уровнях шумов это может привести к ошибочному определению временного положения импульса. Порядок выполнения работы 1. ЛЧМ-сигнал 1) Изменяя длительность импульса (5-30 мкс), несущую (1000-5000 кГц) и частоту девиации (500-3000 кГц) ЛЧМ - определить: скорость нарастания частоты (γ), ширину спектра ЛЧМ-сигнала по графику спектральной плотности, и Базу сигнала ВЛЧМ. Результат занести в таблицу 2.1 Таблица 2.1
2) Разрисовать вид сигнала с ЛЧМ его спектр G() и корреляционную функцию R() ЛЧМ-сигнала. 3) По полученным результатам установить зависимость ширины главного лепестка КФ и базы сигнала от девиации частоты fд Вопросы для защиты лабораторной работы № 2. Сложные сигналы. Определение. Какие сигналы к ним относятся. Почему корреляционная функция R() сложного сигнала уже и выше простого? Почему сложные сигналы называют шумоподобными? ЛЧМ-сигнал. Вид сигнала. Его спектр. База ЛЧМ-сигнала. Корреляционная функция ЛЧМ-сигнала. От чего зависит ширина главного лепестка огибающей корреляционной функции? Недостатки ЛЧМ-сигнала? 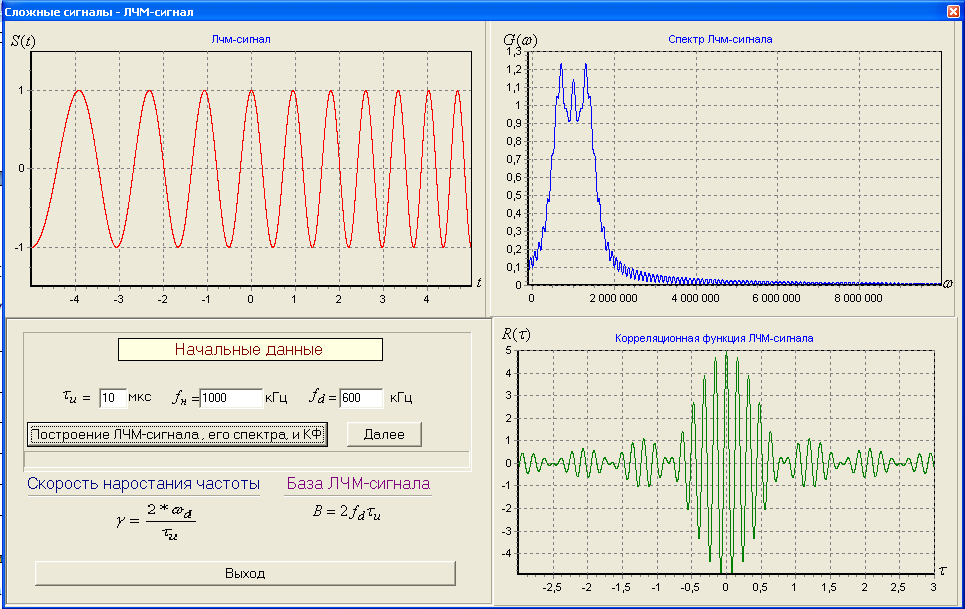 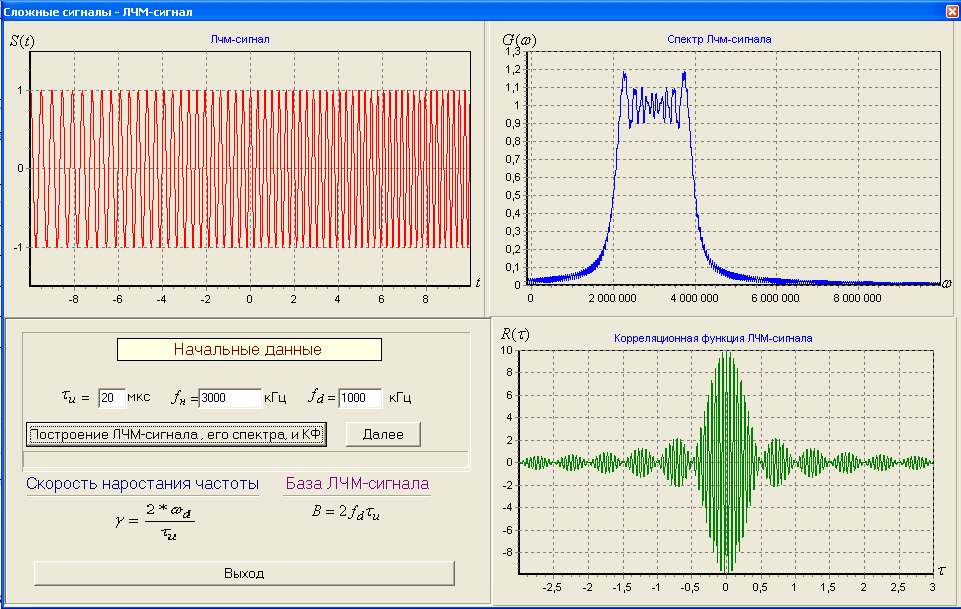 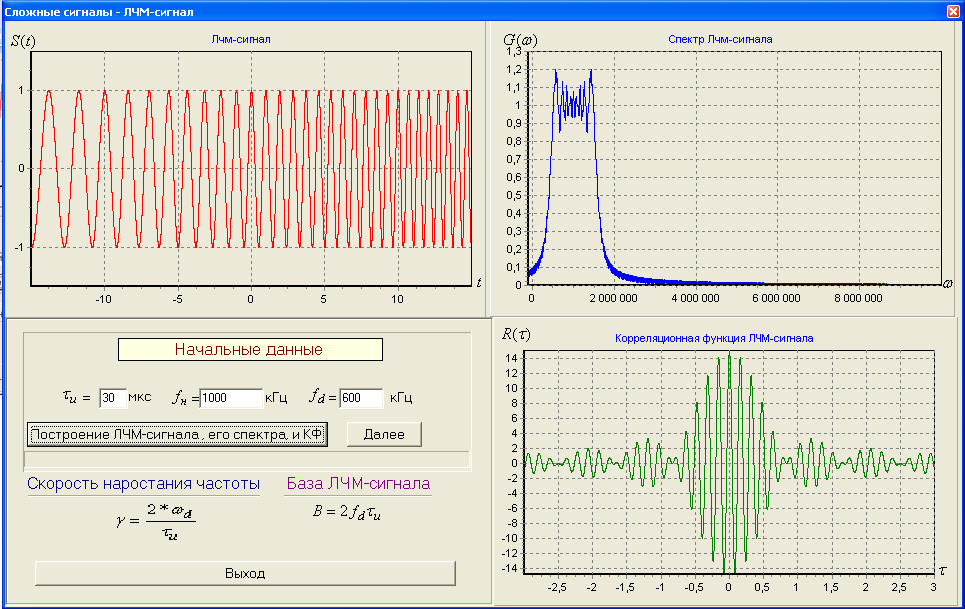 Лабораторная работа № 3. Коды Баркера. Цель работы: Исследование сложных сигналов-кодов Баркера. ТЕОРИЯ Коды Баркера представляют собой сигналы одинаковой длительностью в пределах информационного сигнала (рис. 3.1,а). 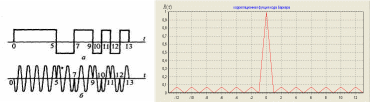 Рис. 3.1 13-ти позиционный код Баркера: а) амплитудное кодирование; б) фазовое кодирование; в) корреляционная функция. При этом коде импульс длительностью иразбивается на несколько элементов одинаковой длительностью, число этих элементов выбирается N=2, 3, 4, 5, 7, 11, 13. Затем этим кодом модулируется по фазе несущая частота, при переходе от посылки к паузе – фаза несущей частоты меняется на 1800 (рис. 3.1,б). Такой сигнал является ШШС и обладает узкой корреляционной функцией R(). От числа N зависит уровень боковых лепестков. Уровень боковых лепестков по отношению к max корреляционной функции (по сравнению с ЛЧМ сигналом) в  раз меньше (рис. 3.1, в). раз меньше (рис. 3.1, в). Математические модели кодов Баркера и отвечающие им КФ приведены в таблице 2
В лабораторной работе корреляционная функция кодов Баркера берется по модулю. Порядок выполнения работы 2. Коды Баркера 1) Изменяя количество элементов кода Баркера, измерить уровень боковых лепестков. Результат измерений занести в таблицу 3.1. Зарисовать вид сигнала (радиоимпульс с огибающей). Таблица 3.1.
Вопросы для защиты Лабораторной работы № 3. Коды Баркера. Что они собой представляют? При каком числе элементов существует код Баркера? От чего зависит уровень боковых лепестков КФ R() кода Баркера? Преимущество при использовании сложных сигналов. 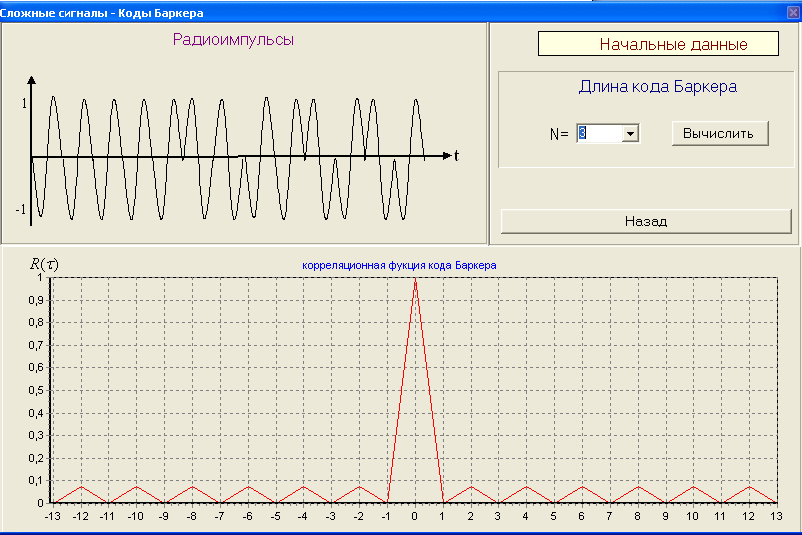 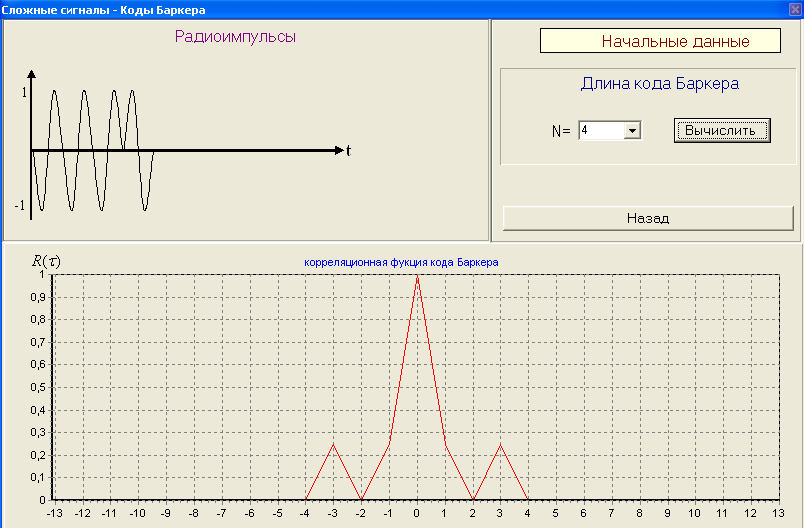 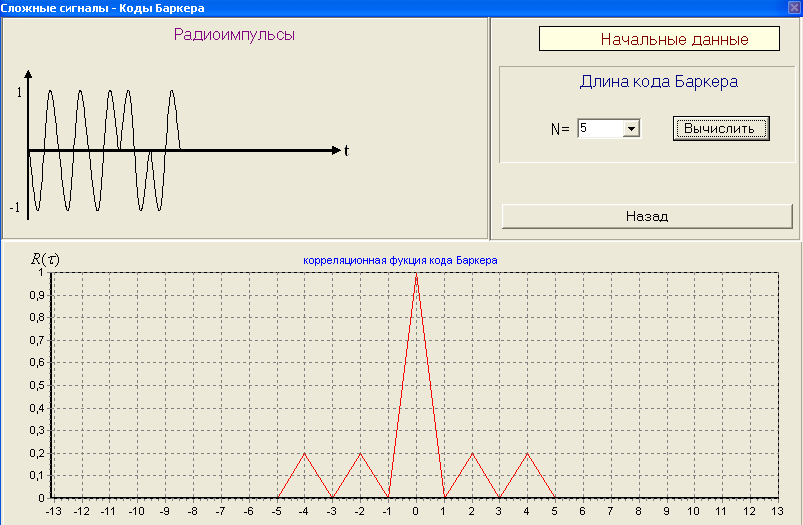 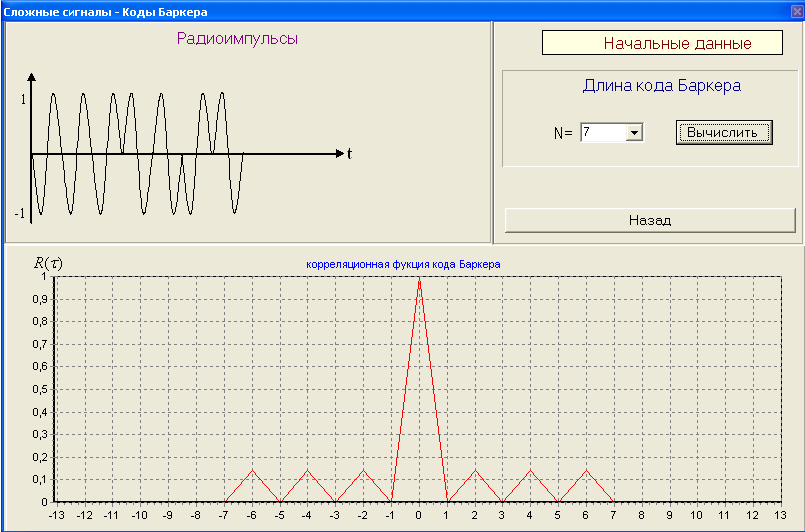 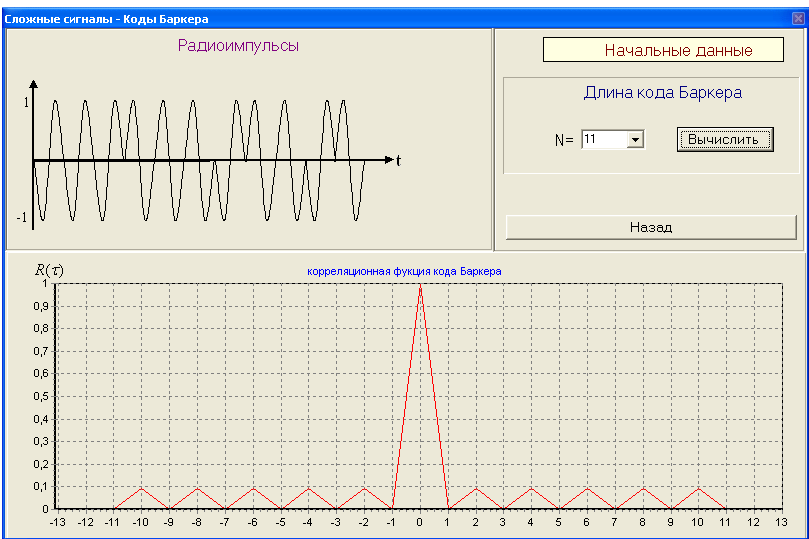 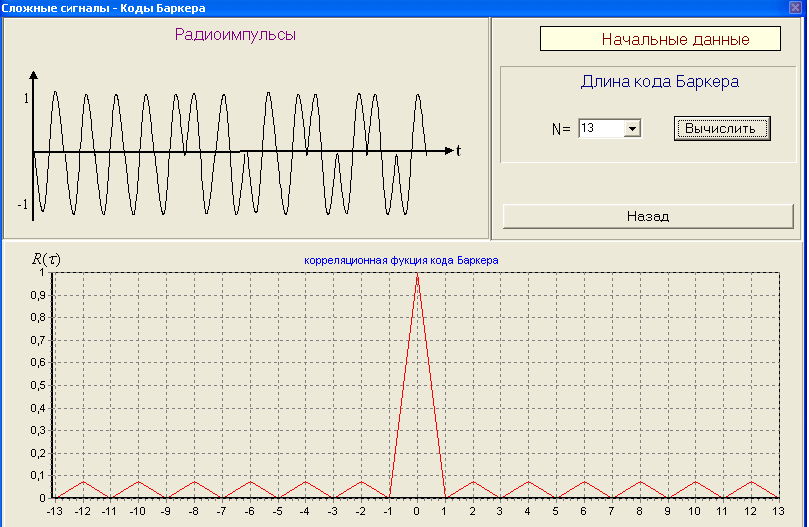 |

 = 0 [B2c]
= 0 [B2c]