Лабораторная работа 2, Коневец Арсений Б9120-09.03.03пикд. Лабораторная работа 2 1
 Скачать 27.52 Kb. Скачать 27.52 Kb.
|
|
Коневец Арсений Лабораторная работа №2 1) Кто-то из C, D, K, T съел кусок пирога. C: K съел D: я не ел K: T съел T: K обманула, когда сказала, что я съел Известно, что только одно высказывание правда. Кто съел? Предположим, что C говорит правду, тогда остальные лгут: возникает противоречие (K съел и D съел). Предположим, что D говорит правду, тогда остальные лгут: возникает противоречие (K утверждает, что Т не ел, а Т утверждает, что К говорит правду, что Т съел). Предположим, что К говорит правду, тогда остальные лгут: возникает противоречие (D съел и Т съел). Предположим, что Т говорит правду, тогда остальные лгут: съел D, так как он сам сказал, а остальные не противоречат ему. 2) 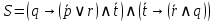 , q = 1, S = 1. Какие значения принимают p, r, t? , q = 1, S = 1. Какие значения принимают p, r, t?Подставим известные переменные и упростим выражение:    3) а)  раскрытие импликации, закон идемпотентности раскрытие импликации, закон идемпотентности , закон расщепления , закон расщепления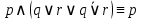 , закон исключенного третьего , закон исключенного третьего , конъюнкция с константой , конъюнкция с константой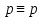 . .б) 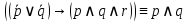 , раскрываем импликацию , раскрываем импликацию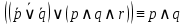 , закон де Моргана и двойное отрицание , закон де Моргана и двойное отрицание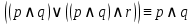 , закон поглощения , закон поглощения . .4) Привести пошаговое доказательство и обоснования    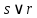  ____________ ____________  – дано (допущение) – дано (допущение)  – 1, 2: MP – 1, 2: MP – дано (допущение) – дано (допущение) – 4, 5: MT – 4, 5: MT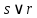 – дано (допущение) – дано (допущение)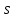 – 5, 6: Disjunctive Syllogism – 5, 6: Disjunctive Syllogism – 7: Disjunctive Amplification – 7: Disjunctive Amplification5) Привести пошаговое доказательство и обоснования:    ____________ ____________  – дано (допущение) – дано (допущение) – дано (допущение) – дано (допущение)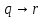 – 1, 2: MP – 1, 2: MP – дано (допущение) – дано (допущение) – 1, 4: MT – 1, 4: MT – 3, 5: MP – 3, 5: MP6) Привести пошаговое доказательство и обоснования:    ____________ ____________  – дано (допущение) – дано (допущение) – дано (допущение) – дано (допущение) – 1, 2: Disjunctive Syllogism – 1, 2: Disjunctive Syllogism – дано (допущение) – дано (допущение) – 3, 4: Disjunctive Syllogism – 3, 4: Disjunctive Syllogism7) Показать, что не справедливо:  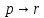 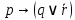  ____________ ____________  – дано (допущение) – дано (допущение)  – 1, 2: MP – 1, 2: MP – дано (допущение) – дано (допущение) – 1, 4: MP – 1, 4: MP – 3, 5: Disjunctive Syllogism – 3, 5: Disjunctive Syllogism – 5, 6: Disjunctive Syllogism – 5, 6: Disjunctive Syllogism8) Доказать, что  . Найти контрпример для обратного утверждения, когда . Найти контрпример для обратного утверждения, когда  , а , а  : :Воспользовавшись универсальной спецификацией, предположим, что  и и  , тогда , тогда  и и  будут истинны для любого a. В этом случае: будут истинны для любого a. В этом случае:  . .9) Показать, что справедливо:   _______________________ _______________________ Так как принимаем предположения и заключение за истину, можем воспользоваться универсальной спецификацией:   _______________________ _______________________  – дано (допущение) – дано (допущение) – 1: Conjunctive Simplification – 1: Conjunctive Simplification – дано (допущение) – дано (допущение) – 2, 3: MP – 2, 3: MP – 4: Conjunctive Simplification – 4: Conjunctive Simplification – 1: Conjunctive Simplification – 1: Conjunctive Simplification – 5, 6: правило конъюнкции (Conjunction) – 5, 6: правило конъюнкции (Conjunction) – правило обобщения – правило обобщения10) 11) Доказать, что n2 - четное тогда и только тогда, когда n - четное для любого натурального n: Если n – четное, то n = 2k, n2 = 4k2 – тоже четное. Докажем обратное: если n – нечетное, то n2 – нечетное. Если n – нечетное, то n = 2k + 1, n2 = (2k + 1)2 = 4k2 + 4k + 1 – нечетное. 12)  . Какие логические значения принимают составные высказывания: . Какие логические значения принимают составные высказывания:а)  ; ;б)  ; ;в)  ; ;г)  ; ;Решим уравнение:    а)  ; ;б)  ; ;в)  ; ;г) 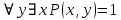 ; ; |
