Численные методы. Численные методы_02_04. Лабораторная работа 2. Численное дифференцирование. Бесконечно гладкая функция f(x) задана несколькими своими значениями y i f(x i )

Название	Лабораторная работа 2. Численное дифференцирование. Бесконечно гладкая функция f(x) задана несколькими своими значениями y i f(x i )
Анкор	Численные методы
Дата	15.08.2022
Размер	32.59 Kb.
Формат файла
Имя файла	Численные методы_02_04.docx
Тип	Лабораторная работа #646115

Численные методы.

Лабораторная работа №2. Численное дифференцирование.

Бесконечно гладкая функция f(x) задана несколькими своими значениями y_i = f(x_i):

X	0	0,2	0,4	0,6	0,8	1,0	1,2	1,4
Y	1	1,0201	1,0811	1,1855	1,3374	1,5431	1,8107	2,1509

Создать аналогичную таблицу с приближенными значениями функции 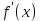, находимыми по формулам:

а) первого порядка точности,

б) второго порядка точности,

оставляя в результате верные цифры и один запасной десятичный знак.

Создать таблицу приближенных значений функции подсчитываемых по формуле второго порядка точности.
Максимально точно, насколько это возможно в данных условиях, вычислить значения производных в контрольных точках второй лабораторной работы: х^* = 1,229; х^** = 0,682.

Выполнение лабораторной работы.

Вычислим производную в узловых точках для левой и правой аппроксимации.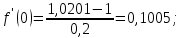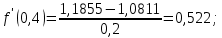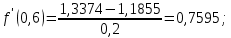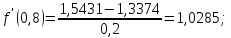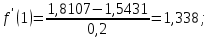

Формула второго порядка точности (симметричная аппроксимация)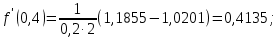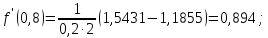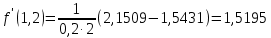

Составим таблицу приближенными значениями

	X	0	0,2	0,4	0,6	0,8	1,0	1,2	1,4
	Y	1	1,0201	1,0811	1,1855	1,3374	1,5431	1,8107	2,1509
Левая аппроксимация			0,1005	0,305	0,522	0,7595	1,0285	1,338	1,701
Правая аппроксимация		0,1005	0,305	0,522	0,7595	1,0285	1,338	1,701
Симметричная аппроксимация			0,2028	0,4135	0,6408	0,894	1,1833	1,5195

Для симметричной аппроксимации в точке f(x₀) и f(x₇) рассчитаем по формуле:

Продифференцируем первую интерполяционную формулу Ньютона: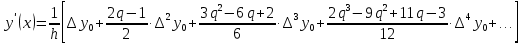

x = 1,229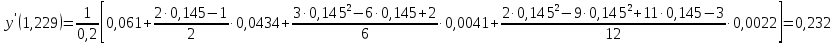

Продифференцируем первую формулу Стирлинга:

Для

x^* = 0,682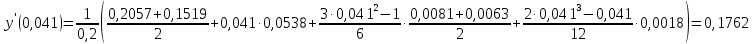

Вывод: в ходе выполнения лабораторной работы были дифференцированы интерполяционные формулы и найдены значения производных в точках х^* и х^**. Также были найдены значения производной в узловых точках, используя методы первого и второго порядка точности.

Лабораторная работа №3. Численное интегрирование.

Дан интеграл

Посчитать сколько достаточно взять узлов, чтобы найти значение интеграла с точностью ε₀ = 10^-4:

а) по формулам прямоугольников (средней точки)?

б) по формулам трапеции?

Вычислить интеграл по этим формулам с заданной точностью.

Вычислить по формуле Симпсона с девятью узлами.

Сравнить результаты пунктов 1 и 2.

Провести сравнительный анализ примененных методов.

Выполнение лабораторной работы.

Находим производные данной функции.

Находим значения второй и четвертой производной на границах интервала.

Выберем максимальное значение второй производной

и максимальное значение четвертой производной

Для формулы прямоугольников определяем шаг и количество отрезков разбиения.

Таблица 1. Метод прямоугольников

1	0,06	1,014087
2	0,18	1,036604
3	0,3	1,051345
4	0,42	1,058328
5	0,54	1,057881
6	0,66	1,050591
7	0,78	1,037236
8	0,9	1,018711
9	1,02	0,995953
10	1,14	0,969885
11	1,26	0,94137
12	1,38	0,911185
13	1,5	0,88
14	1,62	0,848379
15	1,74	0,81678
16	1,86	0,785565
17	1,98	0,755012
18	2,1	0,725327
19	2,22	0,696653
20	2,34	0,669087

Для формулы трапеций определяем шаг и количество отрезков разбиения.

Таблица 2. Метод трапеций

0	0	1
1	0,12	1,026305
2	0,24	1,044953
3	0,36	1,055792
4	0,48	1,059002
5	0,6	1,055046
6	0,72	1,044618
7	0,84	1,028562
8	0,96	1,007802
9	1,08	0,983277
10	1,2	0,955882
11	1,32	0,926442
12	1,44	0,89568
13	1,56	0,864213
14	1,68	0,832552
15	1,8	0,801105
16	1,92	0,770192
17	2,04	0,740051
18	2,16	0,710857
19	2,28	0,682727
20	2,4	0,655738

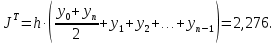Для формулы Симпсона определяем шаг при количестве отрезков разбиения n = 8

Таблица 3. Метод Симпсона

0	0	1
1	0,3	1,051345
2	0,6	1,055046
3	0,9	1,018711
4	1,2	0,955882
5	1,5	0,88
6	1,8	0,801105
7	2,1	0,725327
8	2,4	0,655738

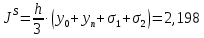Вывод: в процессе выполнения работы были вычислены интегралы методами прямоугольников, трапеций и Симпсона. Составим сравнительную таблицу:

Трапеция	2,276
Прямоугольник	2,198
Симпсон	2,198

Как видим по результатам, значение интеграла, вычисленное различными методами одинаково, что говорит о правильности выполнения работы.