Автореферат. Лабораторная работа 342 определение постоянной ридберга по спектру атомарного водорода
 Скачать 140.43 Kb. Скачать 140.43 Kb.
|
|
ЛАБОРАТОРНАЯ РАБОТА №342 ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ РИДБЕРГА ПО СПЕКТРУ АТОМАРНОГО ВОДОРОДА СОДЕРЖАНИЕ Цель и содержание работы………………………………………..…………..63 Краткая теория работы……………………………………………………..…63 Приборы и принадлежности, необходимые для выполнения работы…..…64 Порядок выполнения работы………………………………………………....67 Обработка результатов измерений………………………………………..….68 Контрольные вопросы………………………………………………………...69 Литература………………………………………………………………….….70 62 Цель работы Ознакомление с закономерностями в спектре водорода. Работа состоит в градуировке спектроскопа, определении длин волн четырех спектральных линий серии Бальмера и расчете постоянной Ридберга. Краткая теория работы Спектры излучения изолированных атомов, например атомов разреженного одно-атомного газа или паров металла, состоят из отдельных спектральных линий и носят название линейчатых. Относительная простота линейчатых спектров объясняется тем, что электроны, входящие в состав таких атомов, находятся под действием только внутриа-томных сил и практически не испытывают возмущающего действия со стороны окружа-ющих удаленных атомов. Изучение линейчатых спектров показывает, что в расположении спектральных линий, образующих спектр, наблюдаются определенные закономерности: линии располагаются не беспорядочно, а группируются сериями. Впервые это было обна-ружено для водорода Бальмером в 1885 г. Сериальные закономерности в атомных спек-трах свойственны не только атому водорода, но и другим атомам и представляют собой проявление квантовых свойств излучающих атомных систем. Частоты всех линий спектра водородного атома можно представить формулой
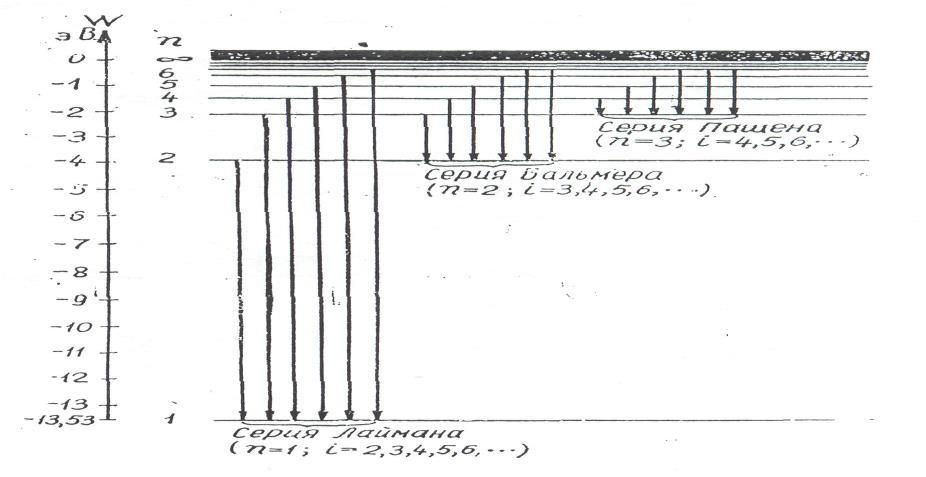 Рис. 1. Схема образования спектральных серий атомарного водорода R– постоянная Ридберга, i – целые числа, причем in. Формула (1) носит название обобщенной формулы Бальмера. Наряду с частотой в спектроскопии принято характеризовать спектральные линии величиной, обратной длине волны, которая носит название волнового числа 1: k = = 1/ = /с. (2) Для волнового числа формула (1) примет вид k = R ( 1/n2 – 1/i2). (3) 63 Формула (3) является обобщением зависимостей, полученных на опыте для отдель-ных серий спектральных линий, например для серии Бальмера в видимой части спектра k = R (1/22 – 1/i2) i = 3,4,5…, серии Лаймана в ультрафиолетовой области k = R (1/12 – 1/i2) n =1, i = 3,4,5…, серии Пашена в инфракрасной области k = R (1/32 – 1/i2) i = 4,5,6… и т. д. Таким образом в обобщенной формуле (3) целое число n дает номер серии, а целое число i номер той или иной спектральной линии в данной серии. Спектральные закономерности в спектре водорода легко объясняются теорией Бо-ра. На рис.1 схематически показано образование серии спектральных линий. Горизон-тальными линиями на рисунке обозначены уровни энергии атома водорода. Стрелками указаны переходы электронов. Согласно теории Бора при переходе электронов с одного энергетического уровня на другой испускается квант энергии с волновым числом:
Сравнивая формулы (3) и (4), получим:
этой формуле все величины выражены в системе СИ. Постоянную Ридберга можно найти с помощью формулы (3), определив экспериментальным путем длины волн в какой-либо серии. Наиболее удобно это сделать в видимой области спектра, т. е. для серии Бальмера. В настоящей работе определяются длины волн первых четырех наиболее ярких спектральных линий серии Бальмера. В этой серии n=2, а i принимает значения: i=3 (крас-ная линия), i=4 (голубая линия), i=5 (фиолетовая линия), i=6 (темнофиолетовая линия, слаборазличимая). Таким образом, постоянная Ридберга определяется из четырех независимых изме-рений. Как будет видно из опыта, значение R при этом получится одинаковым (в пределах точности измерений). Это и означает, что линии серии Бальмера подчиняются сериальной закономерности
Приборы и принадлежности, необходимые для выполнения работы Установка, используемая в работе, состоит из монохроматора УМ-2 и двух спектральных ламп – ртутной и водородной, питание которой осуществляется от специальных устройств. Монохроматор используется в данном случае как спектроскоп, так как выход-ная щель монохроматора заменена окуляром, что позволяет наблюдать спектр визуально. Монохроматор служит в работе для определения длин волн линий в спектре водорода. Оптическая схема монохроматора показана на рис. 2:1 – источник света, 2 – защитное стекло щели, 3 – щель коллиматора, 4 – объектив коллиматора, 5 – диспергирующая 64 призма, 6 – объектив зрительной трубы, 7 – указатель в фокальной плоскости окуляра, 8 – окуляр зрительной трубы. 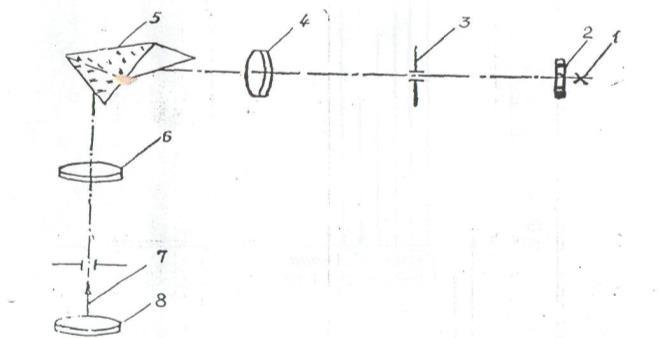 Рис. 2 – Оптическая схема монохроматора Объектив коллиматора, в фокусе которого находится щель, образует параллель-ный пучок света и направляет его на призму 5. Призма преобразует этот пучок в систему параллельных пучков, выходящих из диспергирующего элемента под различными углами, зависящими от длины волны. Объектив зрительной трубы фокусирует отдельные парал-лельные пучки и образует в фокальной плоскости совокупность монохроматических изоб-ражений входной щели, которые и представляют собой спектры, наблюдаемые с помощью окуляра. 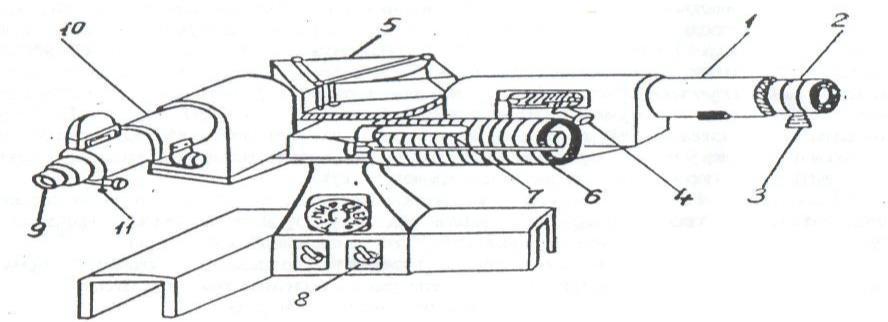 Рис. 3. Общий вид монохроматора Общий вид монохроматора показан на рис. 3: 1 – коллиматор, 2 – щель, величина кото-рой регулируется микрометрическим винтом 3. Винт 4 служит для фокусировки изобра-жения спектральных линий. Поворот призмы 5 осуществляется вращением барабана 6. В зависимости от положения призмы в поле зрения попадает тот или иной участок спектра. На барабане нанесена шкала в относительных делениях – градусах поворота самого бара-бана. Шкала барабана освещается осветителем 7, включение которого производится тум-блером 8. В фокальной плоскости окуляра 9 зрительной трубы 10 находится указатель 11 (см. рис. 2 указатель 7). Спектральные лампы а) Гелиевая лампа. Для того чтобы привести в соответствие деление шкалы бара-бана с длинами волн, монохроматор необходимо проградуировать. Для градуировки ис-пользуется газоразрядная гелиевая лампа с линейчатым спектром излучения. Включение лампы производит лаборант. б) Водородная лампа. В качестве источника света, спектр которого изучается в данной работе, применяется газоразрядная водородная трубка Гейслера. Трубка представ-ляет собой Н -образный стеклянный баллон, заполненный водородом при давлении по- 65 рядка нескольких мм ртутного столба. В колена трубки впаяны электроды, на которые по-дается переменное напряжение 3000 В. В трубке устанавливается тлеющий разряд. В столбе газового разряда происходит диссоциация молекул водорода, атомы которого, воз-буждаясь, излучают характерный для атомарного водорода спектр. Понятно, что молекулы водорода также могут возбуждаться и излучать спектр. Этот молекулярный спектр будет иметь гораздо более сложную структуру (так называе-мый “полосатый” спектр). Но интересующие нас 4 линии серии Бальмера гораздо ярче, чем полосы молеку-лярного спектра, и легко различимы на его фоне. Водородную лампу также включает лаборант. Порядок выполнения работы Градуировка монохроматора. а) Установить против щели монохроматора гелиевую лампу и обратиться к лаборанту с просьбой о ее включении. Вращая винт 4 и перемещая окуляр 9, получить четкое изобра-жение спектральных линий. б) Поворачивая барабан 6, совместить изображение спектральных линий с указателем и произвести отсчет делений по шкале барабана. Эту операцию произвести для всех линий, указанных в таблице, имеющейся на установке. Для правильной градуировки очень важно производить отсчет делений по шкале барабана именно для тех линий, которые изображе-ны на этой таблице и для которых указана длина волны. Данные занести в табл. 1. Для каждой линии отсчет по шкале барабана произвести 3 раза, причем линия к указателю т.е. относительная погрешность εR определяется относительной ошибкой измерения длины волны. Снять показания для 7 линий в спектре гелия. в) Выключить лампу (выполняется лаборантом). Таблица 1.
 
Изучение спектра водорода а) Установить против щели монохроматора гелиевую лампу и обратиться к лаборанту с просьбой о ее включении. б) Вращением барабана 6 совместить с указателем поочередно изображение четырех наиболее ярких линий (красной, голубой, фиолетовой, темнофиолетовой) и произвести отсчет по шкале барабана. Для каждой линии необходимо произвести отсчет не менее трех раз, подводя линию к указателю со стороны больших длин волн. Данные занести в табл. 2. в) После окончания сразу же выключить водородную лампу, так как срок ее службы огра-ничен.
Среднее значение постоянной Ридберга Rср Обработка результатов измерения Построить градуировочный график. Определить по градуировочному графику длины волн четырех измеренных линий спектра водорода. По формуле (3) вычислить постоянную Ридберга, подставляя соответствующие значения n,i. Найти среднее значение R Оценить погрешность измерения R. При оценке погрешности принять во внима-ние следующее. Постоянная Ридберга определяется по формуле (6), т.е. косвенно, путем 67 прямых измерений величин . Согласно элементарной теории ошибок (см. «Лаборатор-ный практикум по физике. Механика», ч.I), относительная погрешность величины
при этом вычисляется по формуле εR= R/R = /, Погрешность измерения длины волны связана со следующими погрешностями: 1)приборной погрешностью; неточностью определения эталонных значений длин волн спектра гелия; погрешностью построения градуировочного графика; погрешностью определения длин волн спектра атомарного водорода по градуи-ровочному графику. Рассмотрим, как влияют все эти погрешности на результат наших измерений. 1. Приборная погрешность является паспортной величиной прибора и не привыша-ет 0,1% для монохроматора, используемого в данной работе. 2. Погрешность в определении эталонных длин волн еще меньше. В настоящее время значения длин волн эталонных источников измерены достаточно точно. Погреш-ность в их измерении не превышает 0,01%. 3. В наших опытах погрешность измерения R определится, главным образом, тре-тьим и четвертым факторами. Рассмотрим влияние масштаба графика на величину ошибки измерения. При выборе масштаба мы должны знать диапазон измеряемой величины. В нашем случае монохроматор градуируется в пределах 3500-6500 А, т. е. диапазон измеряемых длин волн составляет 3000 А. Если мы хотим, чтобы относительная ошибка, вносимая графиком, равнялась приборной, т.е. 0,1%, то это значит, что масштаб графика должен быть выбран таким, чтобы при измерении длины волны в 3500 А единица длины масшта-ба соответствовала 3,5 А. Следовательно, вся ось абсцисс должна содержать столько еди-ний масштаба, сколько отрезков длиной в 3,5 А уложится в интервале 3000 А. В нашем примере этих отрезков уложится 857. Пусть, например, 1 мм соответствует 3,5 А, тогда вся шкала длин волн будет порядка метра. Ясно, что такой график неудобен. Если строить график разумных размеров, то это должно привести к ошибке, превышающей приборную погрешность. Удобно выбрать масштаб таким, чтобы 1 мм по оси длин волн (ось абсцисс) соответствовал 10 А, а 1 мм по оси делений шкалы барабана (ось ординат) соответствовал 10 . Тогда ошибка в определении длины волны будет менее 1%. Контрольные вопросы При каких условиях возникают линейчатые спектры? Какова модель атома по теории Резерфорда-Бора? Сформулируйте постулаты Бо- ра? Выведите на основе теории Бора формулу для энергии электрона на n-ой орбите. Объясните смысл отрицательного значения энергии электрона в атоме. Выведите формулу (4) для спектральных серий атомарного водорода. Изобразите схему образования спектральных серий. Что называется постоянной Ридберга? 68 Каковы трудности теории Бора? Каково устройство монохроматора? Как производится градуировка монохроматора? Что влияет на погрешности измерений в данной лабораторной работе? Как выбирается масштаб градуировочного графика в данной работе? Литература Термодинамика. Электричество и магнетизм [Электронный ресурс]: учебник/ Ташлыкова-Бушкевич И.И.— Электрон. текстовые данные.— Минск: Вышэйшая школа, 2014.— 304 c.— Режим доступа: http://www.iprbookshop.ru/35562.— ЭБС «IPRbooks», по паролю Ташлыкова-Бушкевич И.И. Физика. Часть 2. [Электронный ресурс]: учебник/ Ташлыкова-Бушкевич И.И.— Электрон. текстовые данные.— Минск: Вышэйшая школа, 2014.— 345 c.— Режим доступа: http://www.iprbookshop.ru/35563.— ЭБС «IPRbooks», по паролю | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
